1.4. Кодирование и декодирование кодов

1.4.1. Методы кодирования и декодирования циклических кодов

Операции кодирования и декодирования циклических кодов реализуются с помощью линейных переключательных схем или многотактных линейных фильтров.

Линейные переключательные схемы состоят из трех элементов:

• сумматоров (рис.1.1). Для бинарных кодов суммирование проводится по модулю два;

• умножителей (рис.1.2). Для бинарных схем умножение по существу означает наличие или отсутствие соединения;

• элементов задержки (рис.1.3). Предполагается, что многотактный фильтр синхронизируется тактовым генератором. В элементе задержки информация задерживается на один такт.

Рис.1.1

Рис.1.2

Рис.1.3

Комбинируя операции умножения, сложения и задержки, можно производить различные действия с полиномами.

Умножение некоторой последовательности символов на порождающий полином может быть выполнено с помощью схемы, изображенной на рис.1.4.

Рис.1.4

На рис.1.5 приведена схема, реализующая деление последовательности символов на полином .

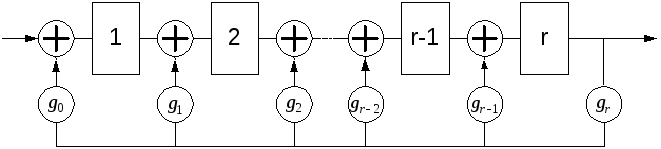
Рис.1.5

Количество элементов задержки в схемах определяется степенью порождающего полинома, а количество сумматоров – числом операций суммирования в полиноме.

Кодовые комбинации в циклических кодах могут быть получены двумя способами:

1. умножением кодовой комбинации простого кода на порождающий полином;

2. умножением кодовой комбинации простого кода 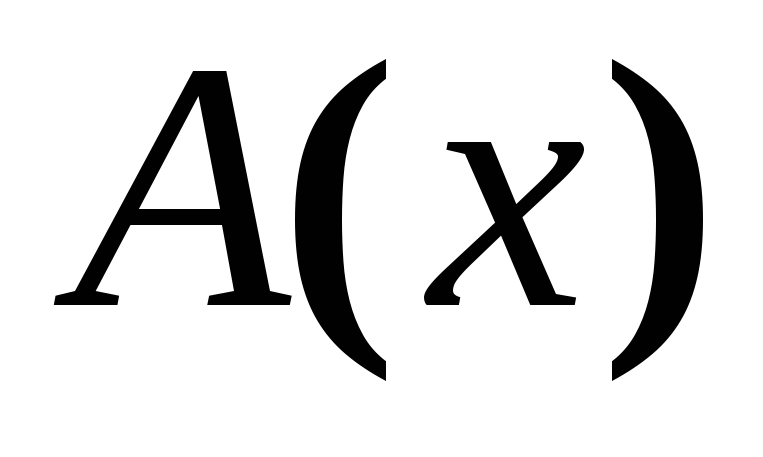на одночлени добавлением к нему остатка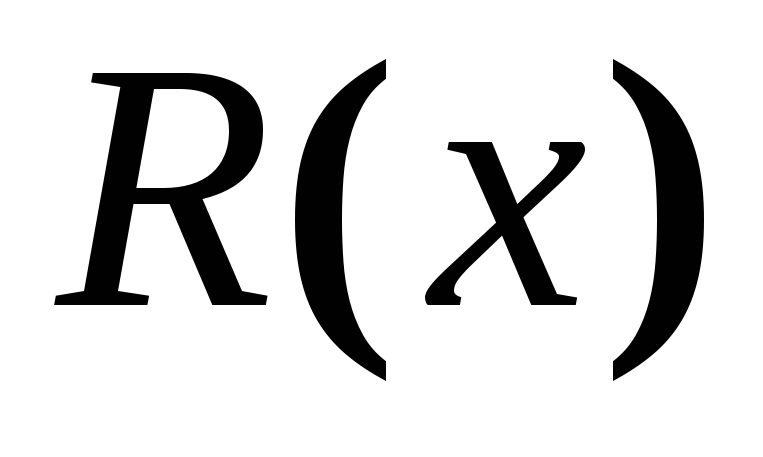, полученного в результате деления произведенияна порождающий полином.

Код, полученный первым способом, является неразделимым, вторым способом – разделимым.

Пример. Получить кодовые комбинации циклического кода (7,4) и построить схемы кодирующего устройства двумя способами, если кодовая комбинация простого кода =, порождающий полиномg(x)=x⁴+x+1.

Способ 1

Кодовая комбинация циклического кода равна:

==.

Другие кодовые комбинации циклического кода могут быть получены путем циклического сдвига данной кодовой комбинации.

Процесс умножения двух полиномов реализуется схемой, показанной на рис.1.6.

Рис.1.6

Для двоичных кодов существенны только те цепи умножения, в которых .

Способ 2

Кодовую комбинацию для получения разделимого кода получают по алгоритму:

1) вычисляют произведение кодовой комбинации простого кода на одночлен:

=.

2) определяют остаток , полученного в результате деления произведенияна порождающий полином:

3) получают кодовую комбинацию:

=+=+.

Кодер может быть реализован по схеме, изображенной на рис.1.7.

Рис.1.7

Схема кодирующего устройства содержит: регистр задержки РЗ информационной группы на четыре такта; формирователь проверочной группы, включающий в себя регистр сдвига РС и сумматоры по модулю два в цепях обратной связи. Два ключа К₁ и К₂ обеспечивают необходимую последовательность работы схемы.

В положении, когда ключ К₁ замкнут, а ключ К₂ разомкнут, информационная часть кода подается на вход схемы, т.е. в первую ячейку регистра задержки РЗ и через сумматор S₁ в первую ячейку регистра сдвига РС. После четырех тактов старший разряд информационной группы находится в последних ячейках обоих регистров. С этого момента ключ К₁ размыкается, а К₂ замыкается. В течение следующих четырех тактов информационная группа поразрядно поступает на выход кодера, а нижняя часть схемы выполняет операцию деления полиномов. По окончании восьми тактов ключ К₂ размыкается, а К₁ замыкается. В течение следующих четырех тактов формирователь проверочной группы «выталкивает» на выход кодера записанные в ячейках регистра РС проверочные разряды, а регистр задержки РЗ заполняется следующими четырьмя разрядами информационной группы.

Декодирование основано на использовании свойства делимости без остатка кодовых комбинаций a(x) циклического (n,k)-кода на порождающий многочлен g(x). Поэтому алгоритм декодирования заключается в делении принятого кодового слова, описываемого многочленом a(x) на многочлен g(x), вычислении и анализе остатка r(x). Если остаток r(x)=0, то принятое кодовое слово считается неискаженным. Если остаток r(x), то принятое кодовое слово стирается и формируется сигнал "ошибка".

Пример. На рис.1.8 изображена схема декодера для циклического кода, заданного порождающим полиномом g(x)=x⁴+x+1.

Рис.1.8