Часть 1. Статически определимые стержневые системы

Задание 1. Расчет многопролетной статически определимой балки

Для балки, выбранной согласно номеру схемы (рис. 1, 2), построить эпюры от заданной нагрузки. Исходные данные выбираются в соответствии с шифром из табл. 2.

Таблица 2

Первая цифра шифра	1	2	3	4	5	6	7	8	9	0
l1, м	10	14	8	12	9	11	7	6	5	13
q, кН/м	1,2	2,0	1,8	3,0	1,5	2,5	1,4	0,8	1,0	2,2
b, м	1,0	0,8	1,9	1,4	1,6	2,1	1,2	1,8	1,5	2,0
Вторая цифра шифра	1	2	3	4	5	6	7	8	9	0
l2, м	8	7	9	6	11	10	12	15	14	14
P, кН	3,0	2,5	6,0	2,8	7,0	3,3	5,0	8,0	4,0	3,2
Третья цифра шифра (№ схемы)	1	2	3	4	5	6	7	8	9	0
a, м	1,0	1,2	2,0	2,2	1,3	2,1	1,4	1,9	1,5	0,8
с, м	1,0	2,2	1,4	1,6	1,8	2,0	1,1	1,3	1,5	1,5
m, кН.м	2,0	2,2	2,7	2,4	2,5	1,1	2,6	3,0	2,8	1,5

Методические указания к заданию.Для построения эпюрQиMв статически определимой многопролетной балке необходимо предварительно определить реакции опор и силы в шарнирах, расчленяя балку на отдельные части и составляя уравнения равновесия для каждой отдельной части. Расчленение балки на части осуществляется по шарнирам. При этом силы взаимодействия между любыми двумя смежными частями балки должны быть равны по величине и противоположно направлены. Выражения дляQиM на каждом участке балки получаются способом сечений:

а) в произвольной точке рассматриваемого участка проводится поперечное сечение;

б) составляются уравнения равновесия для части балки, расположенной с какой-либо стороны от проведенного сечения;

в) из уравнений равновесия для отсеченной части определяются QиM.

При изображении отсеченной части QиMв проведенном сечении показываются в положительных направлениях:Q>0 поворачивает отсеченную часть балки по ходу часовой стрелки;M>0 растягивает волокна с нижней стороны оси балки.

Примечание.Допускается использовать прямой способ получения выражений дляQиM, вытекающий из способа сечений. В прямом способе выражения дляQиMна каждом участке балки записываются непосредственно через силы, действующие с какой-либо стороны от проведенного сечения, с использованием следующих правил знаков:

а) если сила поворачивает часть балки относительно проведенного сечения по ходу часовой стрелки, то она создает в этом сечении поперечную силу Q>0;

б) если сила растягивает волокна в проведенном сечении с нижней стороны оси балки, то она создает в этом сечении M>0.

По полученным выражениям для QиMопределяются их значения в начале и конце каждого участка и затем строятся эпюрыQ,M. Правильность построения эпюр проверяется с помощью дифференциальных зависимостей

, (1.1)

из которых следует:

а) если на участке , то в пределах этого участка, аменяется линейно;

б) если на участке , то в пределах этого участкаменяется линейно, а эпюра- квадратная парабола (способ построения этой параболы показан на рис. 3);

в) если в некоторой точке участка , то эпюрав этой точке имеет экстремум;

г) если в некоторой точке балки действует сосредоточенная сила (нагрузка или реакция опоры), то эпюра в этой точке испытывает скачок на величину данной силы, а эпюраимеет в этой точке излом, обращенный в сторону действия силы.

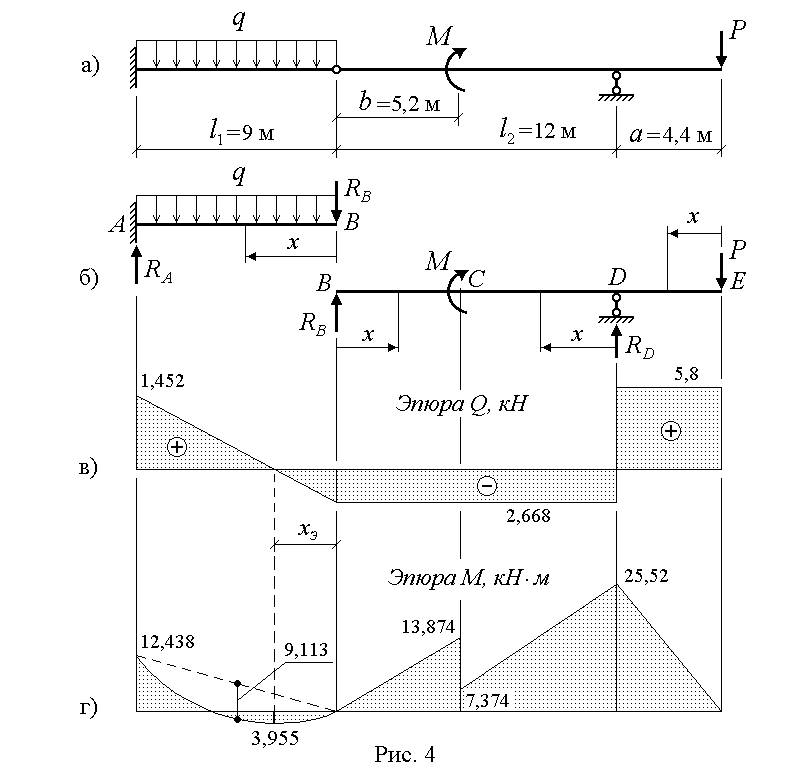
Пример выполнения задания.Дано: схема балки (рис. 4а);

.

Построить эпюры .

Решение.Расчленяем балку на отдельные части по шарнируB(рис. 4б). Для определения реакций опор и силы в шарнире составляем для каждой части по два уравнения равновесия.

Для части BCDE:

Для части AB:

Решая эти уравнения, находим:

.

Записываем выражения для ив произвольном сечении каждого участка. Начало отсчета локальной координаты, определяющей текущее положение сечения на каждом участке, берем в начале участка.

Участок АВ - ход справа:

. Эпюра на участкеABимеет экстремум, положение которого определяется из условия

. Отсюда,.

Участок ВС-ход слева:

.

Участок DE-ход справа:

.

.Участок CD -ход справа:

По данным выражениям определяем значения поперечной силы и изгибающего момента в начале и конце каждого участка (табл. 3) и строим эпюры (рис. 4в, 4г).

Участок	AB		BC		CD		DE
x, м	0	9	0	5,2	0	6,8	0	4,4
Q, кН	-2,668	5,432	-2,668	-2,668	-2,668	-2,668	5,8	5,8
M, кН м	0	-12,438	0	-13,874	-25,52	-7,374	0	-25,52

Таблица 3

Задание 2.Расчет трехшарнирной арки или трехшарнирной рамы

Для трехшарнирной арки или рамы (рис. 5) построить эпюры . Исходные данные выбираются в соответствии с шифром из табл. 4.

Таблица 4

Первая цифра шифра	1	2	3	4	5	6	7	8	9	0
l, м	26	36	18	28	20	32	22	34	24	30
	0,2	0,5	0,3	0,6	0,4	0,7	0,8	0,25	0,35	0,45
Вторая цифра шифра	1	2	3	4	5	6	7	8	9	0
, кН/м	0	4	0	5	0	6	7	0	8	0
, кН/м	4	0	5	0	6	0	0	7	0	8
P, кН	12	9	14	18	20	21	15	19	22	24
Третья цифра шифра	1	2	3	4	5	6	7	8	9	0
Схема	а	а	б	в	г	а	а	б	в	г
	0,34	0,35	0,39	0,40	0,32	0,36	0,38	0,33	0,30	0,31
Очертание оси	П	О	Р	Р	Р	П	О	Р	Р	Р
Обозначения в последней строке: П - парабола; О - окружность; Р - рама.

Методические указания.Для определения в поперечных сечениях трехшарнирых арок или трехшарнирных рам при действии на них вертикальной нагрузки используются следующие формулы:

(2.1)

Здесь - соответственно изгибающий момент и поперечная сила в двухопорной балке длинойравной пролету арки или рамы от заданной вертикальной нагрузки; - распор (горизонтальные реакции);- ордината произвольного сечения; -угол наклона касательной, проведенной к оси арки в произвольном

сечении (для рамы - угол наклона соответствующего прямолинейного участка. В формулах (2.1) считается, что при ;; при

Ордината оси арки, а также значения функций определяются по следующим формулам:

а) при очертании оси по параболе

(2.2)

б) при очертании оси по окружности

(2.3)

Здесь - радиус окружности. Для рамы значенияна каждом участке определяются из геометрических соображений.

Эпюры строятся по точкам. В число расчетных точек обязательно должны входить опоры, шарнир, жесткие узлы рам, точка приложения сосредоточенной силы, а также точки, соответствующие началу или концу участка с распределенной нагрузкой. Всего должно быть 12-14 расчетных точек.

Пример выполнения задания.Дано: схема арки (рис. 6а);

- уравнение оси (па-

рабола). Построить эпюры .

Решение.Записываем уравнения равновесия для определения вертикальных реакций и распора:

Решая эти уравнения, получаем .

Значения в поперечных сечениях арки определяем по формулам

Изгибающий момент и поперечная силаопределяются для двухопорной балки (рис. 6б) от заданной вертикальной нагрузки (реакцииидля балки будут те же, что для арки).

Участок АК (): .

Участок КL(): .

Участок LB():

.

Значения функций ив текущем сечении определяются через тангенс угла наклона касательной к оси арки:

.

Эпюры (рис. 6в, 6г, 6д) строятся по точкам. Результаты расчета сведены в табл. 5.

№ точки	x	y	sin 	cos 	M0	Q0	M	Q	N
-	м	м	-	-	кН м	кН	кН м	кН	кН
0	0	0	0,848	0,530	0	11,040	0	-2,035	-14,291
1	2,1	3,088	0,797	0,604	23,184	11,040	-5,330	-0,746	-14,416
2	4,2	5,544	0,721	0,693	46,368	11,040	-5,191	0,948	-14,404
3	6,3	7,434	0,605	0,796	69,552	11,040	0,416	3,182	-14,084
4	8,4	8,736	0,433	0,902	92,736	11,040	11,491	5,928	-13,162
4	8,4	8,736	0,433	0,902	92,736	-0,960	11,491	-4,890	-7,969
5	10,2	9,384	0,233	0,972	91,008	-0,960	3,737	-3,104	-8,819
6	12,0	9,600	0	1,0	89,280	-0,960	0	-0,960	-9,300
7	14,4	9,216	-0,305	0,952	86,976	-0,960	1,267	1,920	-9,150
8	16,8	8,064	-0,539	0,842	84,672	-0,960	9,677	4,205	-8,351
9	18,6	6,696	-0,661	0,751	78,084	-6,360	15,811	1,369	-11,183
10	20,4	4,896	-0,746	0,666	61,776	-11,760	16,243	-0,895	-14,966
11	22,2	2,664	-0,806	0,592	35,748	-17,160	10,973	-2,673	-19,334
12	24,0	0	-0,848	0,530	0	-22,560	0	-4,070	-24,060

Таблица 5

Задание 3.Расчет плоской статически определимой фермы

Для плоской статически определимой фермы (рис. 7) с выбранными по шифру из табл. 6 размерами и нагрузкой требуется:

1. определить силы во всех стержнях способом вырезания узлов;

б) определить силы в стержнях поясов и раскосе заданной панели способом сквозных сечений.

Таблица 6

Первая цифра шифра	1	2	3	4	5	6	7	8	9	0
l, м	30	28	27	24	21	18	32	33	22	23
P, кН	1,8	1,5	1,2	1,0	1,9	2,0	1,1	1,3	1,4	1,6
Вторая цифра шифра	1	2	3	4	5	6	7	8	9	0
Номер панели (считая слева)	2	3	4	5	2	3	4	5	2	3
Третья цифра шифра (№ схемы)	1	2	3	4	5	6	7	8	9	0
h, м	3,0	5,5	3,5	4,0	6,0	4,2	4,6	4,5	5,0	4,4

Методические указания.В способе вырезания узлов продольные силы в стержнях определяются из уравнений равновесия, составленных для отдельных узлов фермы. В плоскихфермах для каждого узла составляются по два уравнения равновесия:;. Последовательность вырезания узлов должна быть такой, что в каждом узле имелось не более двух неизвестных сил. При расчете предполагается, что все стержни фермы растянуты. Поэтому все продольные силы(i- номер стержня) направляются от узлов. При решении уравнений равновесия, составленных для рассматриваемого узла, найденные ранее значенияподставляются со своими знаками.

В способе сквозных сечений продольные силы в стержнях определяются из уравнений равновесия, составленных для какой-либо отсеченной части фермы. В плоских фермах для отсеченной части можно составить не более трех независимых уравнений равновесия. Поэтому сквозное сечение должно разрезать не более трех стержней. Для определения сил в любом из этих стержней составляются уравнения моментов относительно точки, в которой пересекаются линии действия сил в двух других стержнях. Если из трех разрезаных стержней два расположены параллельно, то для определения силы в третьем стержне составляется уравнение проекций сил на ось, перпендикулярную первым двум стержням. При изображении отсеченной части фермы силы в разрезанных стержнях направляются от узлов.

Пример выполнения задания.Дано: расчетная схема фермы (рис. 8); . Требуется: а) определить силы во всех стержнях способом вырезания узлов;б) определить силы в стержнях поясов и раскосе третьей панели (считая слева) способом сквозных сечений.

Решение.Определяем реакции опор. Из условия симметрии фермы и нагрузки следует, что. Значения углов, необходимые для дальнейших расчетов, определяются из выражений:

Отсюда получаем .

Для определения сил в стержнях способом вырезания узлов рассматриваем последовательно узлы фермы (рис. 9) и составляем для них по два уравнения равновесия (табл. 7).

Из условия симметрии следует, что силы в стержнях правой половины фермы равны силам в соответствующих стержнях левой половины.

Для определения сил в стержнях третьей панели (стержни 10, 11, 12) способом сквозных сечений проведем через данную панель сечение I-I (рис. 8) и рассмотрим равновесие части фермы, расположенной с левой стороны от проведенного сечения (рис.10). Каждую из сил можно определить независимо от двух других, если для рассматриваемой части фермы записать уравнения моментов относительно точекK, O, S:

Здесь

Узел	Уравнения равновесия	Cилы в кН
А
С
D
E
F
K
L

Таблица 7

Из уравнений следует:.

Полученные способом сквозных сечений и способом вырезания узлов значения практически совпадают.

Задание 4.Определение перемещений в статически определимой балке

Для балки (рис. 11) с выбранными из табл. 8 по шифру данными определить прогиб или угол поворота одного из сечений.

Таблица 8

Первая цифра шифра	1	2	3	4	5	6	7	8	9	0
l, м	10,0	8,0	9,6	12,0	12,4	13,0	14,0	15,0	16,0	18,0
q, кН/м	1,0	1,2	1,6	2,0	2,4	2,8	3,0	3,6	5,0	4,0
Вторая цифра шифра	1	2	3	4	5	6	7	8	9	0
P, кН	4,0	4,5	5,0	3,6	2,0	3,2	8,0	6,0	3,0	2,0
№ сечения	1	2	3	1	2	3	1	2	3	1
Третья цифра шифра (№ схемы)	1	2	3	4	5	6	7	8	9	0
Вид перемещения	прогиб					угол поворота

Методические указания.Перемещения (прогибы) и углы поворота сечений балки определяются по формуле Мора

. (4.1)

Здесь - изгибающий момент в произвольном сечении балки от нагрузки;- то же от силы, приложенной в направлении искомого перемещения;- жесткость балки на изгиб. При определении угла поворотазаданного сечения балки изгибающий моментв формуле (4.1) определяется от момента, приложенного в сечении, где определяется угол поворота. Сумма интегралов берется по всем участкам балки. Если на каждом участке, то для вычисления интегралов можно воспользоваться либоправилом Верещагина, либо соответствующими формулами перемножения эпюр.

Первая формула треугольников

. (4.2)

Вторая формула треугольников

. (4.3)

Формула трапеций

. (4.4)

Формула Симпсона

. (4.5)

(Эпюра - квадратная парабола)

При пользовании формулами (4.2) - (4.5) произведения ординат эпюр иберется положительным, если эти ординаты расположены с одной стороны от оси участка. При расположении ординат с разных сторон их произведение берется отрицательным.

Пример выполнения задания.Дано: расчетная схема балки (рис. 12а); . Определить прогиб балки в сечении 1.

Решение.Находимреакции опор от заданной нагрузки:

Из этих уравнений получаем:

.

Проверка:

Определяем значения изгибающих моментов от заданной нагрузки в характерных сечениях каждого участка.

Участок 1А: .

Участок АВ:

Участок CD:

Участок BC: в середине .

По найденным значениям строим эпюру (рис.12б). Затем прикладываем в направлении искомого перемещения (прогиба) силуи строим от нее эпюру изгибающих моментов(рис. 12в). По эпюраминаходим прогиб балки в сечении 1:

Интегралы на участках 1A,ABиBCвычисляются соответственно по формулам (4.2), (4.4) и (4.5).

Задание 5.Определение перемещений в статически определимой раме

Для рамы (рис. 13, 14) с выбранными из табл. 9 по шифру размерами и нагрузкой требуется определить горизонтальное перемещение или угол поворота одного из сечений.

Таблица 9

Первая цифра шифра	1	2	3	4	5	6	7	8	9	0
l, м	9,0	9,5	8,0	8,5	5,0	5,5	6,0	7,5	6,2	6,5
q, кН/м	1,0	1,2	1,5	1,8	2,0	2,4	3,0	2,5	3,2	3,5
Вторая цифра шифра	1	2	3	4	5	6	7	8	9	0
P, кН	9	2	5	4	3	10	7	8	1	6
h, м	6,0	5,5	5,0	9,5	9,0	8,5	8,0	6,5	10,0	7,0
№ сечения	1	2	3	1	2	3	1	2	3	1
Третья цифра шифра (№ схемы)	1	2	3	4	5	6	7	8	9	0
	1:2	2:1	1:3	3:1	2:3	3:2	3:5	5:3	3:4	4:3
Вид перемещения	угол поворота					горизонтальное перемещение

Методические указания.Перемещения и углы поворота сечений рамы определяются по формуле (4.1). Для вычисления интегралов на каждом участке используются формулы (4.2) - (4.5) или правило Верещагина. При известном

соотношении моментов инерции поперечных сечений стержней перемещение и угол поворота выражаются через одну из жесткостей (или). При построении эпюрив рамах необходимо следить за равновесием изгибающих моментов в жестких узлах.

Пример выполнения задания.Дано: расчетная схема рамы (рис. 15а); . Определить горизонтальное перемещение сечения 1.

Решение.Определяем реакции опор от заданной нагрузки:

Определяем изгибающие моменты от заданной нагрузки в характерных сечениях каждого участка.

Участок AD:

в середине -

Участок DB: Участок 1С:

Участок 1ED:

.

По найденным значениям изгибающих моментов строим эпюру от заданной нагрузки (рис. 15б).

Определяем реакции опор от силы , приложенной в направлении искомого перемещения:

Определяем значения изгибающих моментов в характерных сечениях каждого участка рамы от силы.

Участок AD: .

Участок BD: .

Участок 1C: .

Участок 1ED:

.

Строим эпюру от силы(рис. 15в). По эпюрамиопределяем искомое перемещение:

Для вычисления интегралов используются формулы (4.2) и (4.5).