
- •Федеральное агентство по образованию
- •Государственное образовательное учреждение высшего профессионального образования
- •Вятский государственный университет
- •Факультет автоматики и вычислительной техники
- •1804 – "Электропривод и автоматизация
- •II. Программа работы.
- •III. Описание лабораторной установки.
- •II. Программа работы.
- •IV. Описание лабораторной установки.
- •II. Программа работы.
- •IV. Описание лабораторной установки.
II. Программа работы.
-
Изучить алгоритм оптимального по комбинированному критерию управления линейными объектами.
-
Рассчитать фазовые траектории и функции переключения.
-
Ознакомиться с реализацией системы по комбинированному критерию качества.
-
Изучить влияние реальных характеристик элементов и наличия возмущений на поведение системы оптимального управления.
III. Теоретические сведения.
-
Объект управления.
Объектом управления в данной системе является тот же объект, что и в системе оптимального быстродействия (см. п.1 раздел III лабораторной работы №3).
-
Синтез оптимальной оистемы по комбинированному критерию.
Для объекта управления, описываемого уравнениями относительно ошибки
![]() , (8)
, (8)
![]() ,
, ![]() ,
,
определим алгоритм управления, обеспечивающий минимум критерия
![]() , Т
– задано заранее,
, Т
– задано заранее,
при переходе из
начальной точки l10,
l20
в конечную
![]() .
.
В данном критерии первое слагаемое учитывает время переходного процесса, а второе - расход ресурсов на управление за время переходного процесса.
Для определения алгоритма управления применим принцип максимума, с этой целью составим гамильтониан
![]() .
.
Выпишем слагаемые, явно зависящие от управления
![]() .
.
Максимум функции
H'
достигается одновременно с функцией Н
при выполнении следующих условий в
зависимости от значений функции
![]() :
:
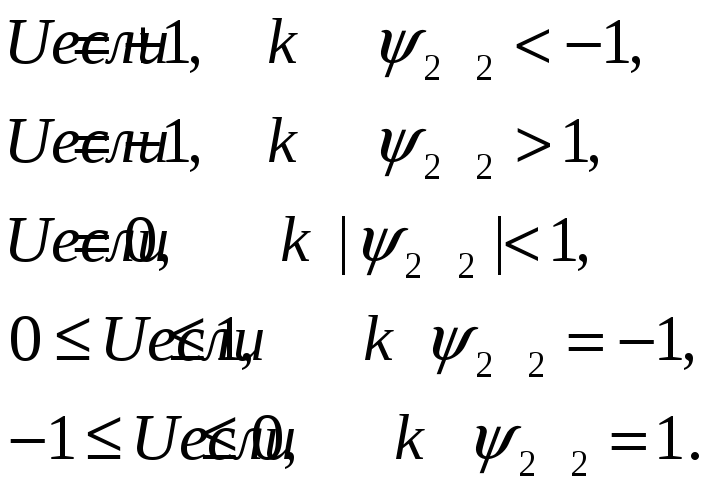
Анализ показывает,
что для рассматриваемого полноотье
управляемого объекта управления условие
![]() не может выполняться на каком-либо
отрезке времени
не может выполняться на каком-либо
отрезке времени
![]() ,
т.е. в системе отсутствуют особые
управления. Поэтому, управляющий сигнал
может принимать только три значения:
+1, 0, -1.
,
т.е. в системе отсутствуют особые
управления. Поэтому, управляющий сигнал
может принимать только три значения:
+1, 0, -1.
Запишем уравнения и соответствующие им решения для сопряженных переменных
![]() (9)
(9)
Графики рис. 13
иллюстрируют один из возможных вариантов
управления. Таким образом, а отличие от
задачи быстродействия, где управление
переключается с одного знака на другой,
в системе с комбинированным критерием
качества имеется интервал времени
![]() на котором управление отключено
на котором управление отключено
![]() ,
что и приводит к уменьшению расхода
ресурсов, т.е.
,
что и приводит к уменьшению расхода
ресурсов, т.е.
![]() .
.
Для определения
моментов переключения и построения
замкнутой системы используем совместно
принцип максимума и метод фазовой
плоскости. В отличие от задачи
быстродействия, в которой использовалась
одна линия переключения, здесь необходимо
иметь две линии переключения: одна -
геометрическое место точек, соответствующих
отключениям управления U=0
на интервале
![]() СОД; другая - геометрическое место точек,
соответствующих переключениям на
торможение, АОВ (рис. 14).
СОД; другая - геометрическое место точек,
соответствующих переключениям на
торможение, АОВ (рис. 14).
Для линии переключения, обеспечивающей переключение на торможение, справедливо выражение, полученное в задаче быстродействия
![]() ,
,
![]() ,
,
![]() . (9а)
. (9а)
Найдем уравнение линии переключения, определяющей моменты отключения управления. Используя решения дня сопряженных переменных (9), найдем постоянную С1
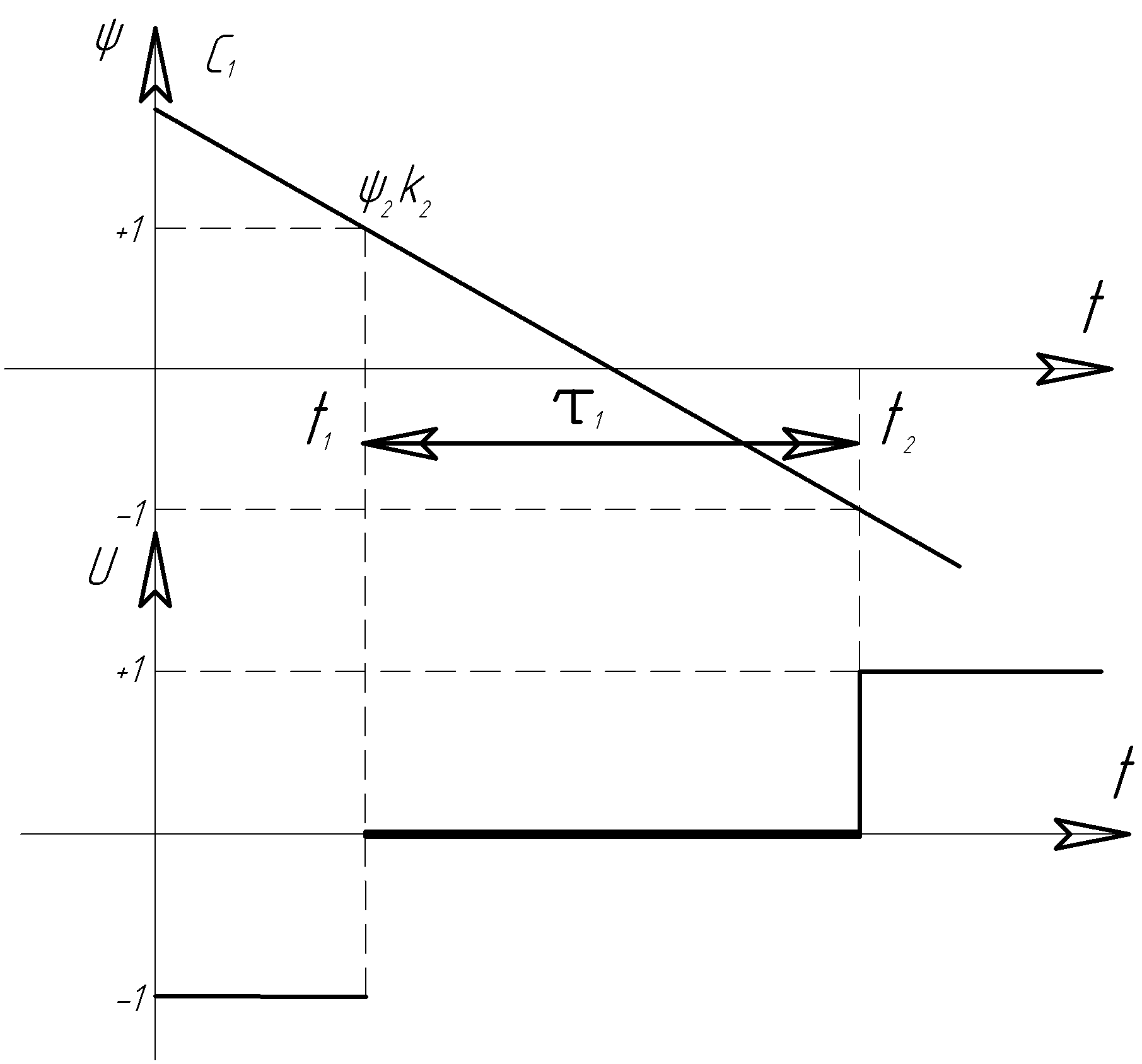
Рис. 13. Закон изменения оптимального по
комбинированному критерию управления

Рис. 14. Фазовые траектории в оптимальной по комбинированному
критерию системе управления
![]()
откуда
![]() ,
,
![]() . (10)
. (10)
С другой стороны, учитывая условие M(t)=0, имеем
![]()
и, следовательно,
![]() (11)
(11)
В результате
сравнения выражении (10) и (11) найдем
длительность интервала τ1,
на котором U=0:
![]()
Иэ фазовых траекторий (рис, 14) следует, что
![]() , (12)
, (12)
где ![]() .
.
Точка
![]() расположена на линии переключения АОВ,
соответствусщей фазовой траектории
торможения, т.е.
расположена на линии переключения АОВ,
соответствусщей фазовой траектории
торможения, т.е.
![]() . (13)
. (13)
Приравнивая
выражения (12) и (13), после подстановки
выражения для τ1
получим зависимость, связывающую
координаты
![]() и
и
![]() в момент отключения управляющего сигнала
в момент отключения управляющего сигнала
![]() ,
|U|=1. (14)
,
|U|=1. (14)
После опускания индекса "о" придем к искомому уравнении линии переключения, на которой происходит отключение управления
![]() , (15)
, (15)
где
![]()
На основе уравнений линий переключения (9а) и (15) запишем функции переключения
![]() , (16)
, (16)
![]() (17)
(17)
В зависимости от граничных условий знаки функций переключения и сигналы управления связаны следующими соотношениями:

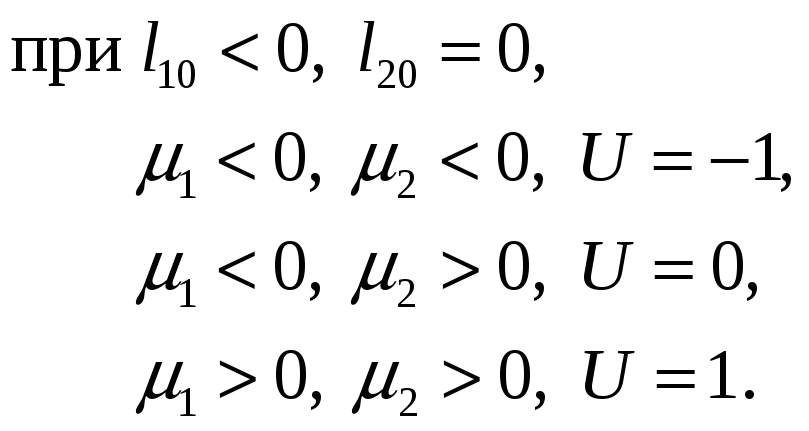
Исходя из полученных выше выражений с учетом уравнений фазовых траекторий; найдем длительности интервалов управления
![]() ,
,
![]()
или после подстановки (15)
 ,
,
 ,
,
 .
.
