3. Обзор приближенных методов поиска экстремума функции многих переменных

3.1. Все приближенные методы поиска экстремума ФМП базируются на следующем итерационном (пошаговом) алгоритме:

, (3)

по которому переход от точки на к-ом шаге к точкена (к+1)-ом шаге осуществляется в направлениис параметром шага в этом направлении^k. Естественно, что направлениеследует выбирать таким образом, чтобы приближаться к экстремальной точке. Выбор шага^kдостаточно произволен, но влияет на скорость приближения к экстремуму. Естественно, алгоритм (3) должен быть сходящимся, т.е. гарантировать попадание в экстремум за конечное или бесконечное число итераций. Такая сходимость получила название алгоритмической.

На рисунке 3 показана геометрическая интерпретация алгоритма (3).

3

Рис. 3

.2. В градиентных методах направление движенияк экстремальной точке выбирается по градиенту или антиградиенту, а шаг^kвыбирается различными способами в зависимости от метода.

Если функция многих переменных дифференцируема, то частные производные первого порядка показывают направление наибольшего возрастания функциив точке. Этот вектор называется градиентомв точкеи представляет собой вектор-столбец, составленный из частных производных:

Каждая частная производная определяет проекцию градиента на соответствующую ось. Если взять значение градиента с обратным знаком, то он покажет направление наибольшего убывания функции (антиградиент).

3.3. Метод наискорейшего спуска.

В методе наискорейшего спуска параметр шага выбирается из условия экстремума функции по градиенту.

Пусть задана сепарабельная (частный случай квадратичной) функция и начальная точка х⁰=(–0,6;–2,6), у⁰=4,68. Матрица Гессе для этой функции:. Матрица положительно определена, следовательно, функция выпуклая и имеет единственный минимум. Вычислим в точке х⁰проекции градиента:

На графике линий равного уровня (рис. 4) строятся проекции градиента в определенном масштабе и результирующий вектор L₁, который дает направление наибольшего изменения функции в точке х⁰. Если провести черезL₁плоскость, перпендикулярную {x₁,x₂}, то эта плоскость, рассекая поверхность, выделит на ней параболу. Далее находится точка экстремума полученной параболы. Для этого следует записать уравнение параболы в данной плоскости (плоскости градиента) с помощью параметра, учитывающего направление антиградиента:

Подставляя значения координат и проекций градиента, получим:

Определим параметр исходя из экстремума функции:

,

Теперь определим координаты точки х⁽¹⁾, в которой функцияпо направлениюL₁достигает экстремума.

,

,

З

Рис. 4

начение функции в этой точке: у⁽¹⁾=1,3. Полученная точка х⁽¹⁾по направлениюL₁показана на рисунке. Линия градиента касается в этой точке линии равного уровня функции у

Продолжая вычисления, а именно: 1) определяя проекции градиента, 2) составляя уравнения параболы в плоскости градиента, 3) находя параметриз условия экстремума функции, 4) определяя координаты точки х⁽²⁾, в которой функцияпо направлению градиента достигает экстремум, получим следующие результаты:

Таблица 1
Итерация	0	1	2	3	4	5
х	(-0,6;2,6)	(-0,08;1,82)	(0,48;2,19)	(0,65;1,94)	(0,83;2,06)	(0,89;1,98)
у	4,68	1,3	0,41	0,14	0,043	0,014

Пусть задана точность по значениям функции у на смежных шагах 0,05. Тогда разность на 4 и 5 итерациях, следовательно, на пятой итерации вычисления можно закончить.

Метод наискорейшего спуска в изложенном выше пошаговом варианте достаточно универсален и применим для широкого класса функций, имеющих конечную производную в каждой точке, т.е. гладких. Но уравнение для иногда получается сложным и громоздким. Для квадратичных функций определениеможно упростить и сделать более удобным для расчетов:

Или:

, (4)

3.4. Градиентный метод с переменным шагом.

Самая трудная операция в методе наискорейшего спуска – нахождение экстремального параметра . Чтобы ее исключить, можно задавать параметрв виде некоторой сходящейся числовой последовательности, например, в виде ряда:

, где n=1,2… – номер итерации, К – коэффициент.

Скорость сходимости данной модификации данной модификации в целом ниже, чем в методе с определением по экстремуму функции у(), и зависит от выбора коэффициента К и самой последовательности. Последовательность должна выбираться такой, чтобы скорость ее сходимости была ниже скорости сходимости градиента, иначе ряд сойдется к 0 быстрее, чем градиент. Для определения коэффициента К желательно определить на первой итерации параметрпо экстремуму у() или по уравнению (4).

3.5. Градиентный метод с постоянным шагом.

Параметр может быть определен на первом шаге, а на последующих итерациях оставаться постоянным. Это еще больше упрощает вычисления.

3.6. Метод сопряженных направлений.

Пусть имеем два направления, которые характеризуются векторами и. Направленияиназывают сопряженными по отношению к некоторой положительно определенной матрице Н, если выполняется соотношение

, (5)

Сопряженность связана с ортогональностью. Если Н – единичная матрица, то при имеем два взаимно перпендикулярных вектора. Соотношение (5) можно трактовать таким образом: матрица Н, примененная к вектору, изменяет его длину и поворачивает на некоторый угол так, что новый вектордолжен быть ортогонален вектору.

Пусть требуется с помощью метода сопряженных направлений найти экстремум функции с начальной точкой. Решение задачи показано на рис. 5.

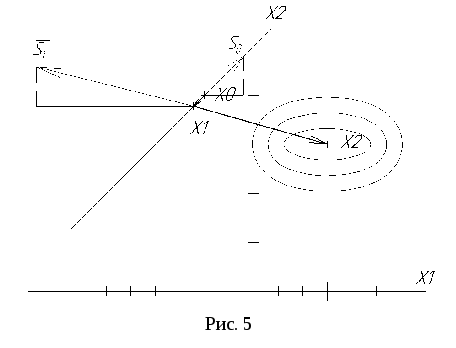
Через произвольно взятый вектор с проекциями==1, отражающий направлениеL₁, проводится плоскость, перпендикулярная плоскости {x₁,x₂}. Плоскость пересечет экстремальную поверхность у(х₁, х₂) и выделит на ней экстремальную линию. Определяются координаты минимума на этой линии (параболе), для чего вычисляются проекции градиента в точке х⁰:

и параметр по (4):

Тогда:

Естественно, линия L₁касается в точке х⁽¹⁾линии равного уровня функции у.

Далее отыскивается сопряженный вектор из условия сопряженности (5):.

Получается одно уравнение с двумя неизвестными. Т.к. важно знать направление вектора, то одной неизвестной задаются произвольно. Пусть =1, тогда= –4. Сопряженный вектор должен проходить через х⁽¹⁾.

Отыскивается экстремум параболы в сечении поверхности у(х₁, х₂) по направлению.

Тогда

Итак, за две итерации было найдено точное значение экстремума функции у. В качестве первого вектора можно было выбрать градиент в исходной точке, процедура поиска при этом остается прежней.

3.7. Метод проекций градиента.

Применяется для решения классической задачи Лагранжа на условный экстремум. Сущность метода проекций градиента состоит в следующем. Если взять в некоторой точке х^ккасательную плоскостьLк ограничению, которая будет характеризоваться нормалью к ней, и градиент функциив этой точке, то проекция разности этих двух величинна касательную плоскость будет характеризовать степень приближения к экстремальной точке.

Ясно, что экстремальной точкой будет такая, в которой проекция градиента на касательную плоскость будет равна 0.

Чтобы попасть в используется следующий алгоритм поиска:

,

где М^(к)– вектор, определяемый как разность градиента и нормали, взятой с весом:

Величина веса наk-ом шаге определяется из условия ортогональности нормали и проекции градиента:

Параметр шага , как и в методе наискорейшего спуска, может быть определен из условия экстремума параболы, полученной в сечении экстремальной поверхности плоскостью, проведенной в направлении М^(k).

Данный метод требует, чтобы начальная точка находилась на ограничении.