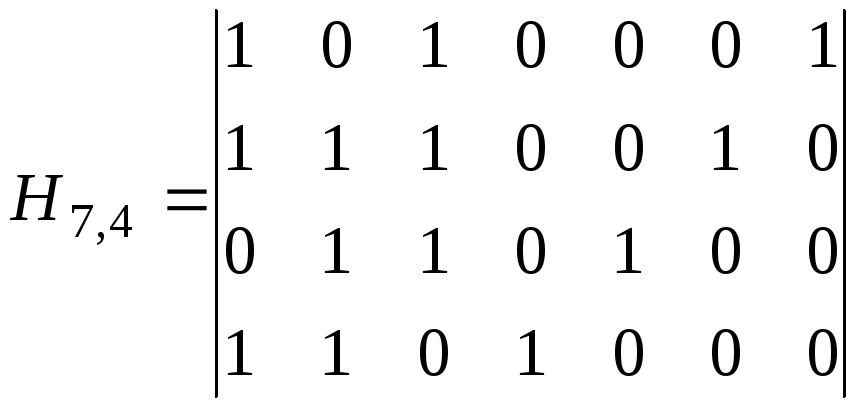Контрольные вопросы к лекции 10

10-1. На что указывает граница Хемминга?

10-2. На что указывает граница Плоткина?

10-3. На что указывает граница Варшамова – Гилберта?

10-4. Почему систематические линейные коды называются групповыми?

10-5. В чем состоит свойство замкнутости группы?

10-6. Как определяются значения контрольных разрядов в каждой кодовой комбинации группового линейного систематического кода?

10-7. Что является особенностью группового линейного систематического кода?

10-8. Чем определяется число проверочных уравнений для группового систематического кода?

10-9. Что задает система проверочных уравнений группового систематического кода?

10-10. Какие кодовые комбинации называются образующими или базисными векторами для того или иного группового линейного кода?

10-11. Почему в качестве образующих удобно выбрать комбинации, которые содержать лишь по одной единице в информационных разрядах?

10-12. Как формируется образующая матрица (n,k)-кода, если задана система проверочных уравнений?

10-13. Как при наличии образующей матрицы можно найти все остальные кодовые комбинации (n,k)-кода?

10-14. Из каких подматриц состоит образующая матрица (n,k)-кода?

10-15. Как может быть сформирована дополняющая матрица (n,k)-кода, если не заданы проверочные уравнения?

10-16. Как, пользуясь образующей матрицей (n,k)-кода, построить систему проверочных уравнений?

10-17. Как, пользуясь образующей матрицей (n,k)-кода, построить проверочную матрицу?

10-18. Как, пользуясь проверочной матрицей (n,k)-кода, построить систему проверочных уравнений?

10-19. Что называется синдромом?

10-20. Какое значение синдрома указывает на наличие ошибки в принятой кодовой комбинации?

10-21. Что называется исправляющим вектором?

10-22. Как можно истолковать содержимое дополняющей подматрицы, пользуясь понятием синдрома?

10-23. Как можно истолковать содержимое единичной подматрицы, пользуясь понятием синдрома?

10-24. Как осуществляется декодирование по максимуму правдоподобия?

10-25. Какие (n,k)-коды называются кодами Хэмминга?

10-26. Что называется радиусом сферической упаковки кода?

10-27. Что называется радиусом покрытия кода?

10-28. Какой код называется совершенным?

10-29. Какой код называется квазисовершенным?

10-30. Как осуществляется укорочение кода?

10-31. Как сказывается укорочение кода на размерах образующей матрицы?

10-32. Как сказывается укорочение кода на размерах проверочной матрицы?

10-33. С какой целью выполняется укорочение кода?

10-34. Как осуществляется расширение кода?

10-35. Как сказывается расширение кода на размерах образующей матрицы?

10-36. Как сказывается расширение кода на размерах проверочной матрицы?

10-37. С какой целью выполняется расширение кода?

10-38. Как образуется расширенный код Хэмминга (8,4) с d=4?

10-39. Как определяется отсутствие ошибок в принятой кодовой комбинации расширенного кода Хэмминга (8,4) с d=4?

10-40. Как определяется наличие двух ошибок в принятой кодовой комбинации расширенного кода Хэмминга (8,4) с d=4?

Лекция 11. Полиномиальные коды

В предыдущей лекции кодовые комбинации (n,k)-кода представлялись в виде набора символов (а₀, а₁, . . .а_n-1) длиной n. Другой способ представления того же кодового слова состоит в том, чтобы элементы а₀, а₁, . . .а_n-1 считать коэффициентами полинома n-1 степени от некоторой фиктивной или формальной переменной x, т.е.

.

Используя это обозначение, можно определить полиномиальный код, как множество всех полиномов степени, не большей n-1, содержащих в качестве сомножителя некоторый фиксированный полином g(x). Полином g(x) называется порождающим полиномом кода.

Для того чтобы иметь возможность умножать кодовые полиномы, разлагать их на множители и производить другие операции, необходимо потребовать, чтобы все коэффициенты полинома были элементами некоторого конечного алгебраического поля. Конечное поле, называемое также полем Галуа и обозначаемое GF(q) – это конечное множество, состоящее из q элементов, в котором определены правила для выполнения арифметических операций. Основное отличие их от обычных арифметических операций состоит в том, что в конечном поле все операции производятся над конечным числом элементов, в связи с чем все конечные поля обладают следующими свойствами:

1. Существуют две операции, используемые для комбинирования элементов – умножение и сложение.

2. Результатом сложения или умножения двух элементов является третий элемент, лежащий в том же поле.

3. Поле всегда содержит мультипликативную единицу 1 и аддитивную единицу 0 , так, что а*1=а и а+0=а для любого элемента а поля.

4. Для любого элемента а поля существует обратный элемент по сложению (-а), такой, что а + (-а)=0 и обратный элемент по умножению а^-1 (при а0), такой, что а* а^-1=1. Существование этих элементов позволяет использовать обычные обозначения для вычитания и деления.

5. Выполняются обычные правила ассоциативности, коммутативности и дистрибутивности.

Конечные поля существуют не при любом числе элементов q, а только в том случае, если число элементов q является простым числом или степенью простого числа. В первом случае поле называется простым, во втором – расширенным. Для каждого допустимого q существует ровно одно поле. Другими словами, правила сложения и умножения, удовлетворяющие всем указанным требованиям можно задать только одним способом. Если q – простое число, то элементами поля являются числа 0, 1, . . . , q-1, а сложение и умножение являются сложением и умножением по модулю q.

С учетом сказанного о полиномиальном представлении кодовых комбинаций и операций над ними для двоичного случая, т.е. над полем GF(2) эти операции выполняются следующим образом.

1. Кодовая комбинация 100101 может быть представлена в виде полинома F(x)=1*x⁵+0*x⁴+0*x³+1*x²+0*x¹+1*x⁰b = x⁵+x²+1.

2. Сложение таких полиномов осуществляется следующим образом. Пусть, например, f₁ = x⁷+x⁴+x³+x+1, а f₂ = x⁵+x⁴+x²+x, тогда f₃=f₁+f₂ = x⁷+x⁵+x³+x²+1. В двоичном виде 10011011  00110110 = 10101101.

3. Умножение полиномов. Пусть, например, f₁ = x³+x²+1 и f₂ = x+1, тогда f₃=f₁*f₂ = x⁴+x³+x+x³+x²+1 = x⁴+x²+x+1. В двоичном виде (1101)*(11)=(01101)  (11010) = 10111. Циклический сдвиг некоторого полинома, а он, напомним, форма представления кодовой комбинации, соответствует простому умножению этого полинома на x.

4. Деление полиномов. Пусть, например, f₃ = x⁴+x²+x+1, а f₂ = x+1, тогда f₁= f₃/f₂ = x³+x²+1, что можно продемонстрировать, выполняя деление полиномов столбиком или делая то же самое в двоичном виде.

При некоторых значениях n полиномиальные коды обладают свойством цикличности и называются циклическими. Свойство цикличности состоит в том, что если кодовая комбинация а_n, а_n-1, . . . , а₁ является разрешенной кодовой комбинацией данного кода, то и кодовая комбинация, а_n-1, . . . , а₁, а_n, получаемая из нее путем циклического сдвига, тоже будет разрешенной кодовой комбинацией данного кода. Сдвиг обычно осуществляется справа налево, причем крайний левый символ переносится в конец комбинации. Число возможных циклических (n,k)- кодов значительно меньше числа различных групповых (n,k)- кодов.

При использовании циклических кодов процесс кодирования, так же, как и в рассмотренных (n,k)- кодах, сводится к определению значений n-k контрольных разрядов на основании известных значений k информационных разрядов для каждой кодовой комбинации.

При полиномиальном представлении этот процесс осуществляется следующим образом. Полином f(x), отображающий комбинацию безызбыточного двоичного кода умножается на x^n-k. Это приводит к увеличению длины кодовой комбинации на n-k разрядов, которые и используются в качестве контрольных. Далее произведение f(x)* x^n-k делится на некоторый полином g(x), названный ранее образующим, и остаток от этого деления r(x) суммируется с произведением f(x)* x^n-k. Полученная кодовая комбинация описывается полиномом,

,

(3.21)

который без остатка делится на образующий полином g(x).

Сказанное является важным свойством циклических кодов, используемым при декодировании для обнаружения или исправления ошибок.

Пример 3.5

Пусть n=7, k=4, g(x)=x³+x²+1. Найти кодовую комбинацию s(x), если ее информационная часть описывается полиномом f(x)=x³+x+1.

Решение. 1) n-k=7-4=3, тогда f(x)* x^n-k = (x³+x+1)x³ = x⁶+x⁴+x³.

2) с остатком r(x)=x². 3) Таким образом, искомая кодовая комбинация =x⁶+x⁴+x³+x² или в двоичном виде 1011100, где левые четыре разряда представляют собой информационные разряды, соответствующие полиному f(x)=x³+x+1, а остальные три разряда – контрольные, соответствующие полиному r(x)=x².

Таким образом, выявлено первое свойство образующего полинома g(x), состоящее в том, что все разрешенные комбинации данного кода делятся на него без остатка. Он позволяет выбрать из большого числа комбинаций только те, которые удовлетворяют заданному закону построения кода, т.е. разрешенные. Именно поэтому полиномg(x)и называется образующим.

Степень lобразующего полиномаg(x)не может быть меньше требуемого числа контрольных разрядовn-k. Для упрощения обычно полагаютl=n-k. Но не любой полином этой степени может выступать в качестве образующего полинома циклического кода. В качестве таковых могут использоваться только так называемые неприводимые полиномы. Полином называется приводимым, если он может быть представлен в виде произведения полиномов низших степеней, в противном случае полином называется неприводимым. Другими словами, неприводимый полином делится без остатка только на самого себя и на единицу. Неприводимые полиномы играют роль, сходную с простыми числами в теории чисел. Из нескольких неприводимых полиномов данной степени в качестве образующего полинома следует выбирать самый короткий, однако число ненулевых членовg(x)не должно быть меньше требуемого кодового расстояния кода.

Циклические коды являются подклассом рассмотренных ранее групповых систематических (n,k)-кодов. Следовательно, кроме полиномиального описания, они могут быть описаны с помощью образующей и проверочной матриц.

Образующая матрица циклического кода может быть построена методом, аналогичным рассмотренному ранее.

Пример 3.6. Построить образующую матрицу циклического кода (7,4) с образующим полиномом g(x)=x³+x+1.

Решение.

Запишем базовые информационные комбинации

0001

0010

0100

1000

Представим их в виде полиномов

1

x

x2

x3

Умножим на x^n-k=x³

x3

x4

x5

x6

Поделим каждый из них на образующий полином и зафиксируем остаток

	Частное	Остаток
	1		011
			110
			111
			101

Тогда образующая матрица этого кода может быть представлена следующим образом

,

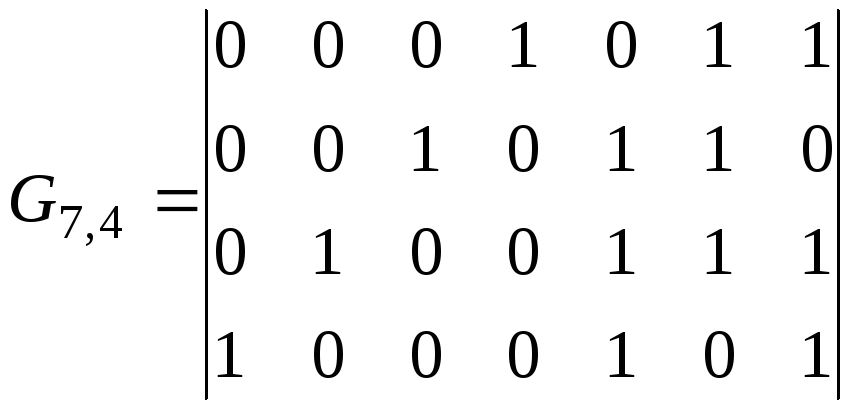или в общем виде

.

Существует другой способ построения образующей матрицы, базирующийся на основной особенности циклического (n,k)-кода. Первая строка образующей матрицы формируется путем приписывания слева к представленному двоичным кодом образующему полиному k-1 нулей. Каждая следующая строка образуется циклическим сдвигом предыдущей строки на один разряд влево. Для того же образующего полинома g(x)=x³+x+1 образующая матрица, построенная таким способом, будет выглядеть следующим образом

.

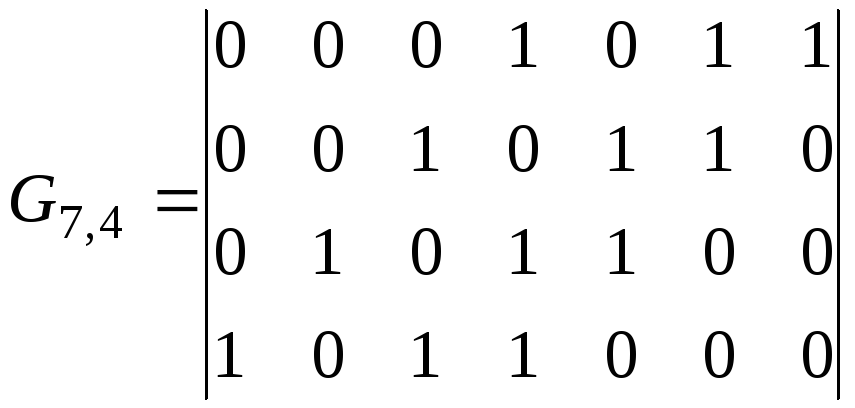Рассмотренный метод проще, но получающаяся матрица менее удобна для использования. Такой вид образующей матрицы в отличие от предыдущего называется неканоническим.

Метод получения канонической формы проверочной матрицы циклического кода аналогичен рассмотренному ранее общему для групповых кодов методу, т.е.

.

Тогда для рассматриваемого циклического кода с образующим полиномом g(x)=x³+x+1 проверочная матрица будет выглядеть следующим образом

.

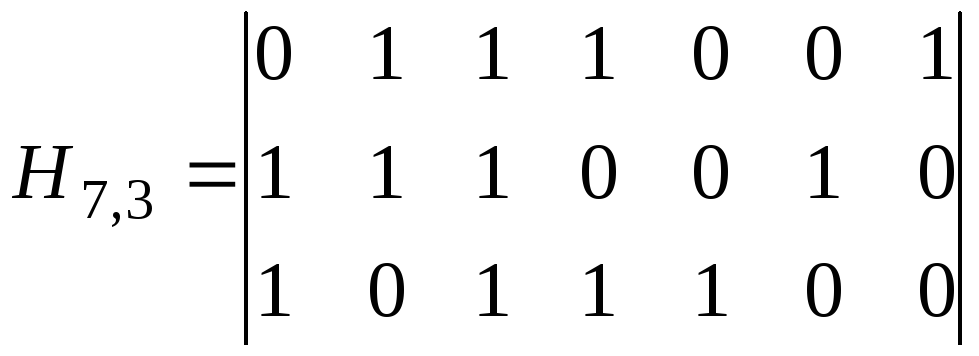Идея обнаружения ошибок в кодовой комбинации циклического кода основана на сформулированном ранее утверждении, что при отсутствии ошибок принятая кодовая комбинация совпадает с переданной , т.е. Без остатка делится на образующий полиномg(x).

При наличии ошибок переданная комбинация преобразуется в, где- полином ошибок, содержащий столько членов и на тех позициях, в которых не совпадают элементы переданной и принятой комбинаций.

Следовательно, при делении наg(x) получим

.

При наличии однократной ошибки в каком либо информационном разряде полиномы ошибок имеют вид:

1

x

x2

x3

Деление этих полиномов на образующий уже было выполнено ранее. С этих позиций можно по-другому взглянуть на содержимое образующей матрицы. Если строки единичной подматрицы рассматривать как полиномы ошибок, то соответствующие строки дополняющей подматрицы представляют собой остатки, указывающие на ошибку в разряде, указываемом полиномом ошибки. Таким образом, остаток от деления полинома принятой кодовой комбинации на образующий полином играет роль синдрома, что свидетельствует о возможности применения к циклическим кодам метода синдромного декодирования.

Возможность матричного описания циклических кодов указывает на то, что кодеры и декодеры циклических кодов могут быть построены на основе этого писания методами, рассмотренными ранее.

Из полиномиального описания циклических кодов следует, что процессы кодирования и декодирования этих кодов представляют собой операции деления полиномов. Для аппаратной реализации операции деления полиномов используются циклические регистры сдвига, т.е. последовательные регистры с обратной связью, в цепи которой устанавливаются сумматоры по модулю два.

Методы построения кодеров и декодеров таких кодов исследуются в лабораторной работе №8 «Кодеры и декодеры циклических кодов» [1. с. 78-85].

Циклические коды, будучи подклассом линейных групповых кодов, так же как и рассмотренные ранее коды, могут быть подвергнуты в зависимости от требований системы, в которой они используются простым преобразованиям, среди которых ранее упоминались расширение кода и укорочение кода. В некоторых случаях преобразования может получиться код, в котором циклический сдвиг его кодовой комбинации не всегда приводит к другой разрешенной кодовой комбинации. Такие коды называются псевдоциклическими.

Для увеличения кодового расстояния циклического кода может быть использовано преобразование расширения кода, выполняемое за счет введения дополнительных контрольных разрядов. Одним из простейших способов расширения кода является введение одного контрольного разряда общей проверки на четность. В результате, например, циклический код (7,4) с образующим полиномом превратиться в циклический код (8,4) с образующим полиномом, поскольку полином(x+1) является образующим для циклического кода с одним контрольным разрядом, способным обнаруживать все ошибки нечетной кратности. Отсюда (попутно) можно сделать вывод о том, что код с проверкой на четность является циклическим кодом с образующим полиномом (x+1). Полученный расширенный код с d=4 будет обладать такими же корректирующими свойствами, что и аналогичный расширенный код Хэмминга. Можно сделать обобщение, состоящее в том, что для любого кода с нечетным кодовым расстоянием введение общей проверки на четность увеличивает кодовое расстояние на 1.

Если далее над этим кодом выполнить операцию укорочения, состоящую в удалении одного информационного разряда, то получится код (7,3) с d=4 и проверочной матрицей

.

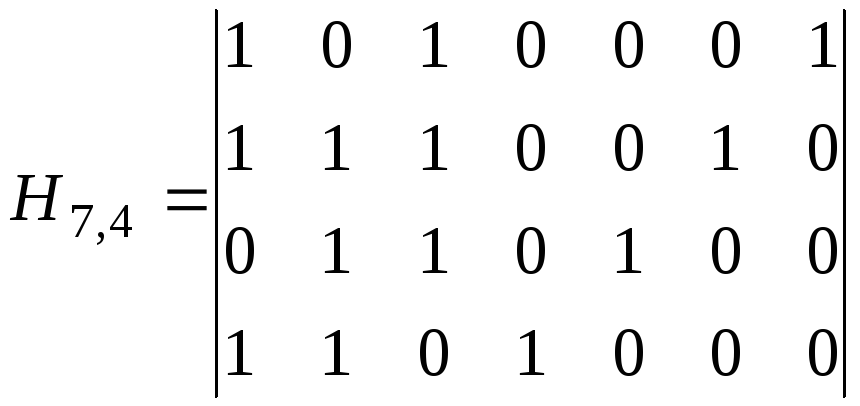Этот код приведен здесь, во-первых, в качестве примера выполнения простых операций по преобразованию кодов, а во-вторых, для того, что с его помощью проще всего продемонстрировать еще один метод декодирования, отличающийся от рассмотренного ранее синдромного метода, и называемый методом мажоритарного декодирования.

Метод мажоритарного декодирования применим тогда, когда систему общих контрольных проверок удается за счет использования различных линейных комбинаций из уравнений, входящих в нее, изменить так, что для каждого символа a_j может быть построена система уравнений

,

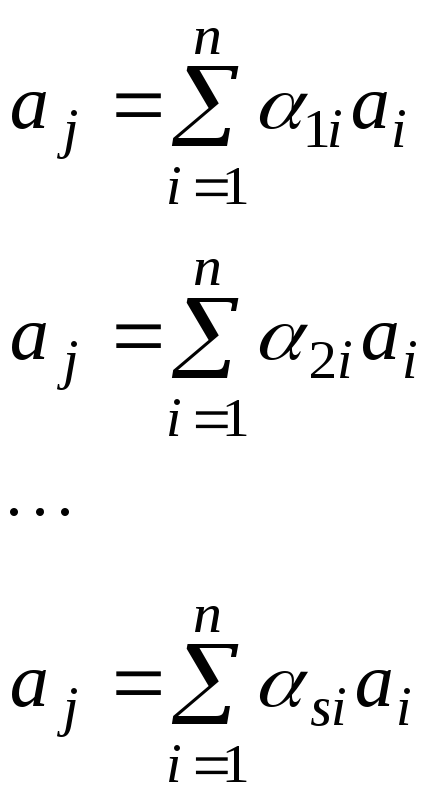называемая системой раздельных контрольных проверок и обладающая тем свойством, что в правую часть каждого уравнения входят символы, отличные от a_j, и всякий такой символ входит не более, чем в одно уравнение. Такая система проверок называется ортогональной.

Если число уравнений, входящих в каждую ортогональную систему, не меньше s, то путем голосования по большинству могут быть исправлены любые ошибок. В самом деле, ошибка в одном символе влияет в силу ортогональности не более чем на одну проверку, следовательно, среди значений символаa_j , которые получены из всех s проверок неправильными могут оказаться не более t, т.е. Не более половины уравнений. Тогда, сравнивая значения правых частей проверок, а также значение самого символа a_j, можно по большинству значений определить верное значение этого символа. Если при нечетном s имеет место равенство голосов, то ошибка обнаруживается, но не исправляется.

Случай, когда число s проверок в каждой ортогональной системе на единицу меньше кодового расстояния s=d-1 является в известном смысле идеальным. В этом случае голосование позволяет полностью реализовать корректирующие свойства кода. Код, для каждого символа которого существует система из d-1 ортогональных проверок, называется полностью ортогонализируемым.

Именно к таким кодам относится код (7,3), проверочная матрица которого получена ранее в результате последовательных операций расширения и укорочения циклического кода.

Пользуясь ею можно записать систему проверочных уравнений

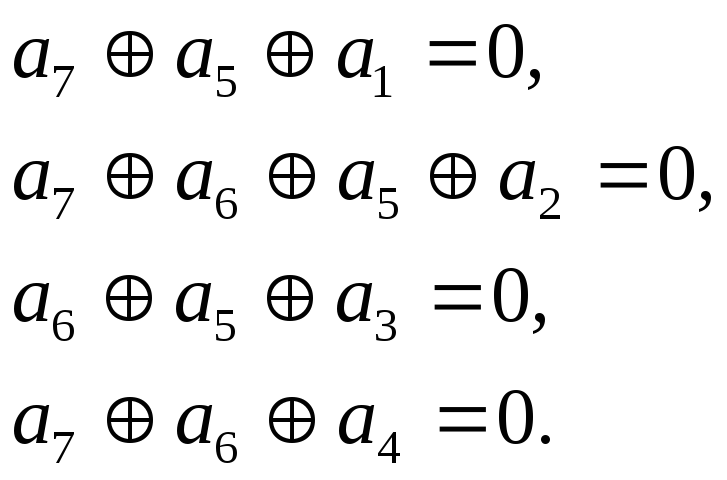
Суммируя по модулю два второе и третье уравнения и разрешая полученные три уравнения относительно а₇, получаем систему

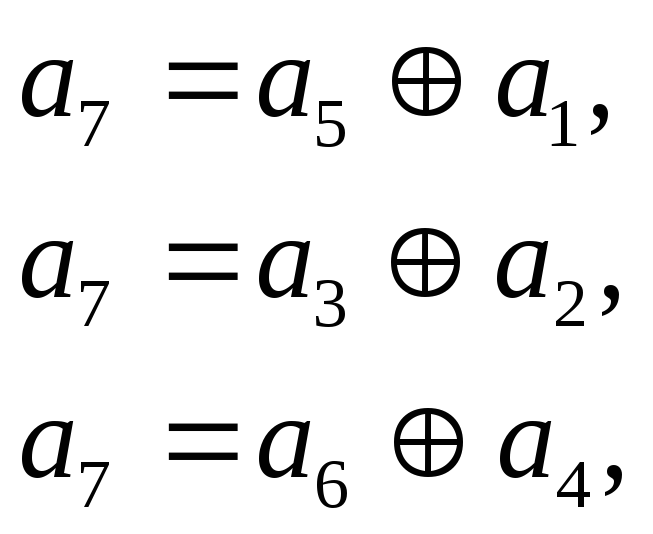
отвечающую сформулированным ранее условиям ортогональности.

Такие ортогональные системы могут быть достаточно просто в силу свойства цикличности составлены для всех символов кодовой комбинации, т.е. уравнения циклически сдвигаются в индексах с выполнением операции по модулю n.

Анализируя указанным выше способом каждый символ принятой кодовой комбинации можно правильно восстановить посланную кодовую комбинацию, если произошло не более одной ошибки, или обнаружит двойную ошибку. Тем самым полностью реализуются корректирующие способности этого кода, поскольку его кодовое расстояние d=4.

Метод мажоритарного декодирования отличается простотой технической реализации особенно в случае двоичных циклических кодов. Наряду с регистром сдвига для приема кодовой комбинации и совокупностью сумматоров по модулю два, которые реализуют ортогональную систему проверок, декодер должен содержать мажоритарный элемент. Для рассматриваемого примера функция мажоритарного элемента описывается таблицей истинности.

1 проверка	2 проверка	3 проверка	М
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Важнейшие классы других полиномиальных кодов

Коды БЧХ

Циклический код, исправляющий более одной ошибки, т.е. код с d  5, в общем случае можно построить следующим образом:

а) по заданному k определить необходимое для исправления одной ошибки n-k и построить (n,k)-код описанным ранее методом;

б) рассматривая этот (n,k)-код как некорректирующий n-разрядный код, определить количество n₁-n дополнительных контрольных разрядов для обеспечения исправления одной ошибки в этом коде и построить тем самым (n₁,n)-код;

в) повторяя данную процедуру t раз, можно получить код, исправляющий независимые ошибки кратности до t включительно.

Однако код, построенный таким образом, не будет оптимальным с точки зрения количества контрольных символов при данной величине k, т.е. будет обладать излишней избыточностью. Минимальное число контрольных символов при данном k и данной корректирующей способности может быть получено при использовании одной из разновидностей полиномиальных кодов, называемой кодами Боуза – Чоудхури – Хоквингема или БЧХ-кодами.

Заданными при кодировании с помощью БЧХ-кодов является число ошибок t, которое требуется исправлять, и общая длина кодовой комбинации n. На выбор величины n накладывается ограничение: n=2^f – 1, где f – любое целое число больше нуля. Число информационных символов k и число контрольных символов n-k и их состав подлежат определению.

При заданной величине t кодовое расстояние кода может быть определено следующим образом:

и названо конструктивным кодовым расстоянием, которое может быть и меньше реального кодового расстояния.

Образующий полином g(x) БЧХ-кода находится как наименьшее общее кратное (НОК) так называемых минимальных полиномов до степени 2t-1 или d-2 включительно, т.е. g(x) = НОК [M_i(x)], где i = 1,3,5, . . ., 2t-1 – номера минимальных полиномов. Поскольку минимальные полиномы по определению являются простыми и неприводимыми, то, условившись об отбрасывании возможных одинаковых M_i(x), можно НОК заменить произведением полиномов , число которых в этом произведенииL=t, а степень полинома g(x) равна .

Знак нестрогого равенства появился как результат того, что степени некоторых M_i(x) могут быть меньше 2t-1.

Далее можно определить число контрольных разрядов n-k, которое по определению равно степени образующего полинома, т.е. n-k = , после чего становится возможным и определение числа информационных разрядов k=n-(n-k). Если получившееся k окажется меньше требуемого для передачи заданного объема информации, необходимо перейти к следующему по порядку разрешенному n=2^f – 1 и выбрать для формирования g(x) минимальные полиномы степени f. Далее по описанной ранее методике для обычных циклических кодов при известном g(x) могут быть построены образующая и проверочная матрицы кода и, тем самым, код полностью построен и описан. Минимальные полиномы различных степеней являются справочными данными.

Для декодирования БЧХ-кодов могут быть использованы как алгоритмы анализа остатка от деления и мажоритарного декодирования, так и другие алгоритмы.

Единственным известным на настоящий момент совершенным БЧХ-кодом является БЧХ-код (23,12) с кодовым расстоянием, равным 7, и образующим полиномом g(x)=x¹¹ + x⁹ + x⁷ + x⁶ + x⁵ + x + 1 или g(x)=x¹¹ + x¹⁰ + x⁶ + x⁵ + x⁴ + x² + 1. По имени создателя он получил название кода Голея.

Важнейший подкласс БЧХ-кодов образуют коды Рида – Соломона, являющиеся недвоичными БЧХ-кодами. Они достаточно широко используются в системах двухуровневого каскадного кодирования.

Коды максимальной длины

Кодами максимальной длины называются циклические коды с параметрами (2^k-1, k), у которых в качестве образующего полинома выбран проверочный полином, полученный описанным ранее образом. Например, требуется построить код (15,4) максимальной дины. Выбрав по описанным выше правилам примитивный полином четвертой степени, например x⁴ + x + 1, найдем для него проверочный полином, который и будет образующим полиномом для кода (15,4) максимальной длины

.

Этот полином является полиномом кодовой комбинации кода. Остальные 14 ненулевых кодовых комбинаций являются четырнадцатью циклическими сдвигами этой комбинации (полинома). Отсюда вытекает одно важное свойство этих кодов. Поскольку все ненулевые комбинации являются циклическими сдвигами одной ненулевой комбинации, то все комбинации этого кода имеют один и тот же вес. Такие коды называются эквидистантными или симплексными.

Кодеры для таких кодов иногда называют регистрами сдвига с линейными обратными связями, формирующими последовательности максимальной длины. Они имеют несколько различных применений. При большом числе разрядов такой регистр формирует последовательность с очень хорошими свойствами случайности. Такие устройства используются на практике в качестве генераторов псевдослучайных последовательностей.

Коды Файра

Подкласс полиномиальных кодов, разработанный для обнаружения и исправления пакетов ошибок, называется кодами Файра.

Пакетом ошибок длины b называется последовательность b символов, в которой крайний слева и крайний справа символы обязательно искажены, а любые из b-2 символа, заключенные между ними могут быть как искаженными, так и неискаженными.

Образующий полином кода Файра определяется выражением

,

где g(x)- неприводимый полином степени l, причем l>b, где b- длина исправляемого пакета ошибок, а c2b-1, причем с должно выбираться таким, чтобы оно не делилось нацело на число e=2^l-1. Число контрольных разрядов в кодовой комбинации кода Файра определяется по формуле n-k = c+l, а общее число разрядов в кодовой комбинации n находится как наименьшее общее кратное чисел с и е, т.е. n = НОК(с,е).

Сверточные коды

Все рассмотренные ранее помехоустойчивые коды относились к блоковым кодам. Отличительной особенностью блоковых кодов является то, что закодированная последовательность символов представляет собой последовательность кодовых комбинаций (блоков) одинаковой длины n, каждая из которых кодировалась независимо от других. Иначе обстоит дело при использовании сверточных кодов. Дополнительные символы в таких кодах зависят от ряда предшествующих информационных символов, в результате чего передаваемая последовательность становится одним полубесконечным кодовым словом.

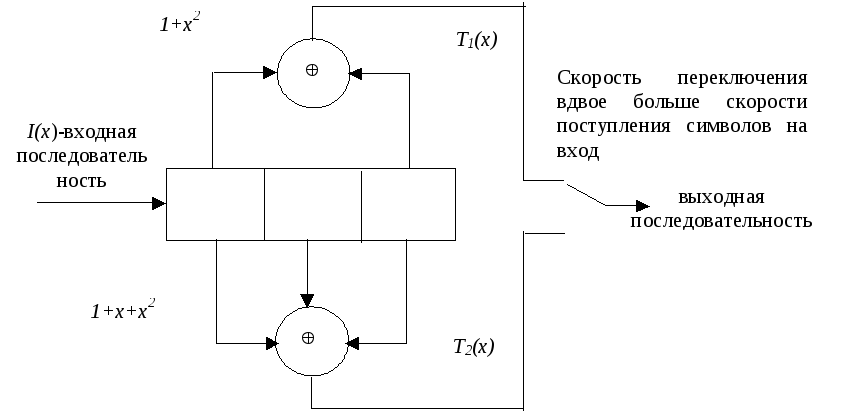
Построение сверточных кодов лучше всего рассмотреть на примере работы кодера, который любым k₀ символам входной информационной последовательности ставит во взаимно однозначное соответствие n₀ символов выходной последовательности. Простейший сверточный кодер (рис. 3.2) представляет собой регистр сдвига с m разрядами, в котором символы кодовой последовательности формируются суммированием по модулю два значений с выходов некоторых разрядов регистра.

Рисунок 3.2. Сверточный кодер

Сверточные кодеры (и коды) характеризуются скоростью кодирования R=k₀/n₀, означающей, что если в каждый момент времени (такт) k₀ символов входного кода поступают в регистр, то за это же время с выхода снимается n₀ символов выходного кода. Для данного примера R=k₀/n₀ = 1/2, т.е. поступление каждого символа на вход приводит к появлению двух символов на выходе. Другой важнейшей характеристикой является длина кодового ограничения или просто кодовое ограничение, равное числу разрядов регистра m, в связи с чем эту характеристику называют иногда памятью кода. Величина n_a = m*n₀ называется полной длиной кодового ограничения. Величина полного кодового ограничения характеризует протяженность корреляционных связей в кодированной последовательности для одного информационного символа. Если на вход кодера подавать различные информационные последовательности и каждый раз на длине n_a выходной последовательности фиксировать ее вес, то минимальный зафиксированный вес даст значение т.н. cвободного кодового расстояния d_св.

Связи между разрядами регистра и сумматорами по модулю два удобно описывать порождающими полиномами. Для приведенной схемы и. При таком представлении символы на входе кодера могут быть получены путем умножения входной последовательности на порождающие полиномы, т.е.и. Рассматриваемый в примере сверточный код является несистематическим, поскольку ни, нине совпадают с входной последовательностью. Для получения систематического сверточного кода необходимо было бы положить или, или, т.е. убрать один из сумматоров, чтобы информационная входная последовательность стала частью выходной.

Рассматриваемый сверточный кодер под воздействием нулевой входной последовательности будет выдавать нулевую выходную последовательность. Если, например, подать в кодер один символ 1, за которой последуют нули, то выходная последовательность будет иметь вид

	1 такт	2 такт	3 такт	4 такт
Сост. регистра	100	010	001	000
Т1	1	0	1	0
Т2	1	1	1	0

Таким образом, входная последовательность 1000 . . . порождает выходную последовательность 1101110000 . . . .

Порождающая матрица кода может быть построена аналогично ранее рассмотренным, но в виде полубесконечной матрицы

.

Выходная последовательность, соответствующая произвольной входной последовательности может быть получена путем суммирования по модулю два соответствующих сочетаний строк этой матрицы.

Таким образом, сверточный код, формируемый этим кодером, имеет следующие параметры:

- скорость кодирования R=1/2;

- кодовое ограничение m=3;

- полное кодовое ограничение n_a=6;

- свободное кодовое расстояние d_св=5.

Другой способ описания связей между входной и выходной последовательностями сверточного кодера состоит в использовании кодового дерева, в котором каждая вершина соответствует очередному входному символу, а на ребре, ведущем к этой вершине, записывается соответствующая совокупность выходных символов. Таким образом, каждая входная последовательность задает некоторый путь на дереве, а совокупности символов, соответствующие ребрам, составляющим этот путь, образуют выходную последовательность. Ясно, что при росте длины входной последовательности число возможных путей растет экспоненциально, так что использование такого дерева не очень удобно.

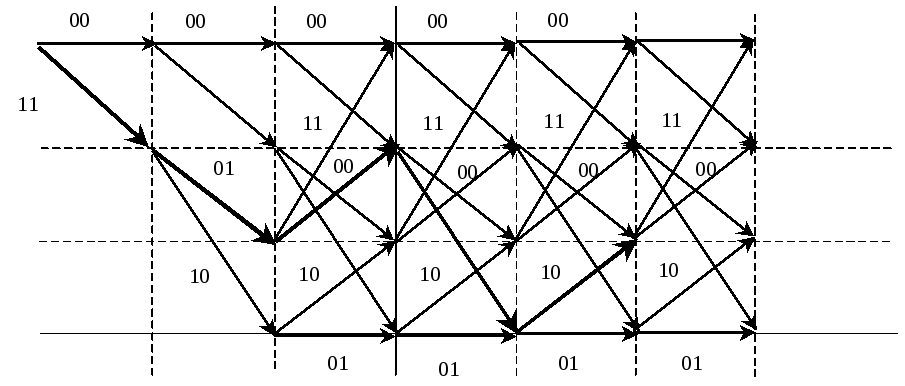
Более удобным является представление в виде т.н. решетчатого графа. Решетчатым называют граф, узлы которого находятся в узлах прямоугольной координатной сетки, т.е. образуют строки и столбцы. Граф полубесконечен справа, т.е. число столбцов полубесконечно. Число узлов в каждом столбце, т.е. число строк конечно и равно , гдеm - длина кодового ограничения. Конфигурация ребер, соединяющих узлы каждого столбца с узлами столбца справа, одинакова для всего графа. На основании сказанного построим решетчатый граф (рис. 3.3) для кодера, приведенного ранее, условившись, что из двух ребер, выходящих из каждого узла, верхнее соответствует входному символу 0, нижнее – 1.

Рисунок 3.3. Решетчатый граф

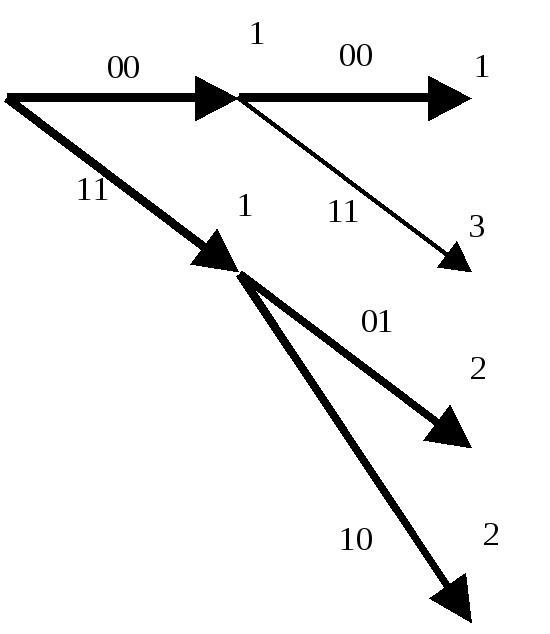
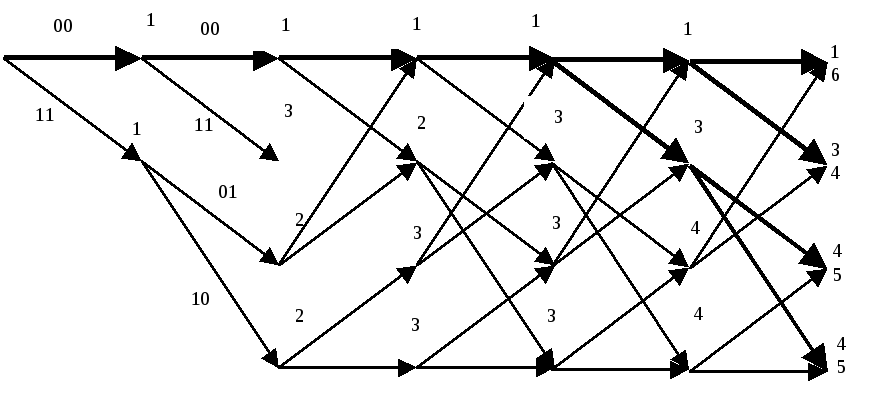
Продемонстрируем процесс кодирования с помощью решетчатого графа, например, кодируя входную комбинацию =101100 . . ., т.е. Выходная комбинация, найденная по графу (жирные линии) будет 1101001010, что можно проверить, воспользовавшись построенной ранее образующей матрицей и сложив по модулю два 1, 3 и 4 ее строки

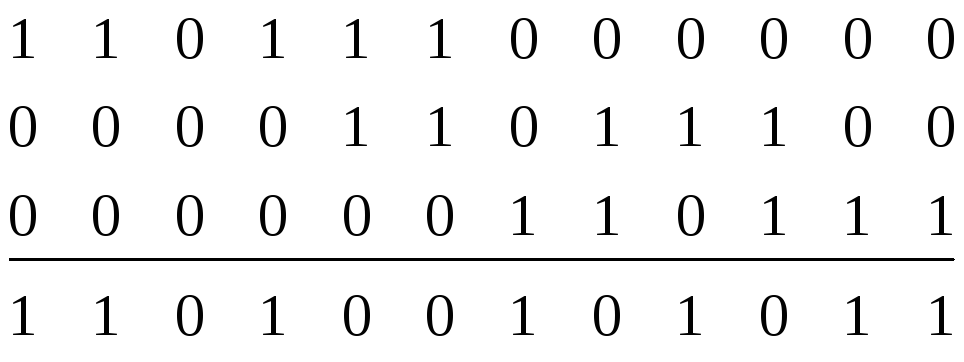
Развитие теории сверточных кодов происходило в трех направлениях в соответствии с тремя важнейшими методами декодирования сверточных кодов:

- метода декодирования по максимуму правдоподобия;

- метода последовательного декодирования;

- метода порогового декодирования.

После введения сверточных кодов встал вопрос о том, какие коды – сверточные или блоковые потенциально лучше. Ответ на этот вопрос был дан Витерби, который получил границы вероятности ошибки для сверточных кодов и с их помощью показал, что характеристики оптимальных сверточных кодов как функции кодового ограничения лучше соответствующих характеристик блоковых кодов той же длины. Для получения этих характеристик Витерби использовал алгоритм декодирования сверточных кодов, который действует как алгоритм декодирования по максимуму правдоподобия.

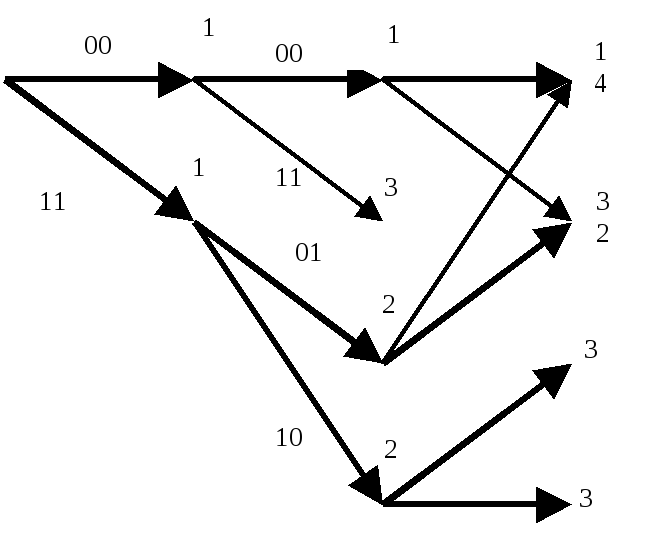
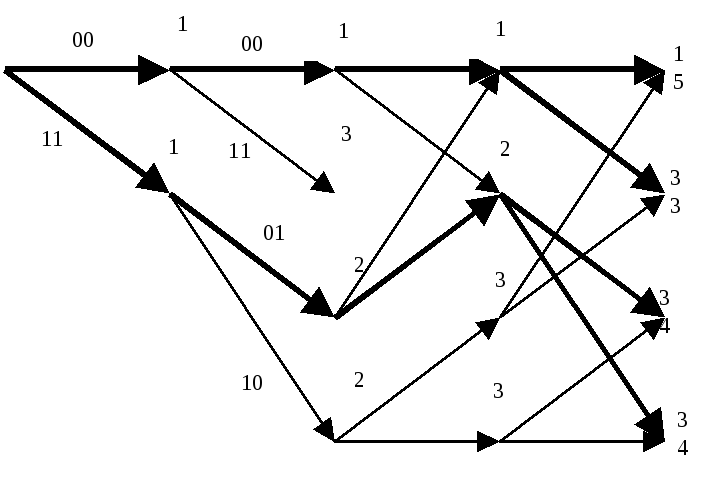
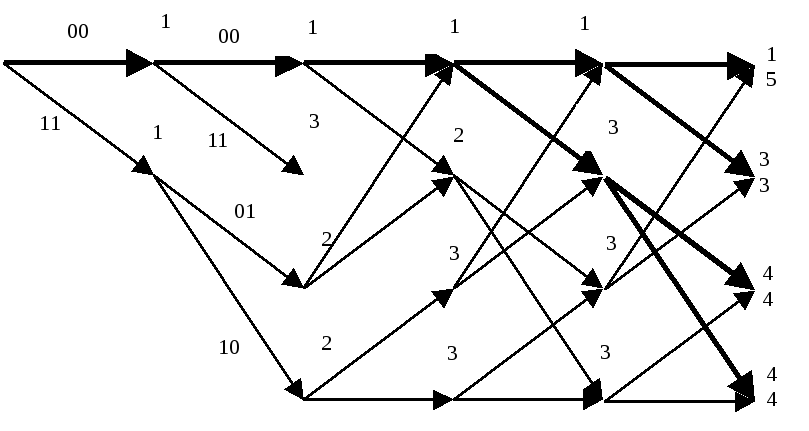
Задачу декодирования сверточного кода можно рассматривать как задачу нахождения пути на решетчатом графе с помощью некоторых правил декодирования. Как и в случае декодирования блоковых кодов по максимуму правдоподобия целесообразными оказываются попытки выбрать правильный путь, который лучше всего согласуется с принятой последовательностью, т.е. попытки минимизировать вероятность ошибки последовательности. Поскольку с ростом длины последовательности число путей растет экспоненциально, то на первый взгляд задача построения оценки последовательности по максимуму правдоподобия для сверточного кода кажется безнадежной. Однако метод построения такой оценки достаточно легко найти, пытаясь непосредственно вычислить метрику для каждого пути на решетке. Вначале число путей действительно растет экспоненциально с ростом длины последовательности. Однако вскоре появляется возможность исключить из рассмотрения такое число путей в каждой вершине, которое в точности уравновешивает число вновь появившихся путей. Таким образом, оказывается возможным иметь сравнительно небольшой список путей, который всегда будет содержать наиболее правдоподобный путь. Эта итеративная процедура декодирования называется алгоритмом Витерби. Проще всего рассмотреть функционирование алгоритма Витерби на примере уже приведенной решетчатой диаграммы для кода с R = 1/2 и m=3. Заметим, что в ней имеется ровно по два пути, ведущих в каждую вершину уровня 4. Поскольку, начиная с этого уровня, соответствующие пути совпадают, декодер максимального правдоподобия может без потери общности принимать решение соответствующее этой вершине. После того, как это сделано, аналогичная процедура может быть применена к следующему уровню и т.д. Именно таким образом работает алгоритм Витерби. Согласно ему на каждом уровне сравниваются два пути, входящие в каждую вершину, и сохраняется лишь тот из них, метрика которого лучше. В качестве метрики может служить расстояние Хэмминга между принятой последовательностью и кодовыми словами, считываемыми с ребер решетки. Другой путь с худшей метрикой исключается из рассмотрения. Оставшиеся пути называются выжившими. Для рассматриваемого кода с m=3 в каждый момент будет сохраняться не более 4 выживших путей.

Для упрощения демонстрации работы алгоритма Витерби положим, что передавалась нулевая последовательность 00000000. . . , а принятой оказалась последовательность с одной ошибкой 10000000. . . .

Тогда работа алгоритма может быть описана следующими фрагментами:

1) принимаемый кадр n0 символов – 10. Декодер выберет оба пути и определит метрику каждого из них – цифра над узлом;

2) принимаемый кадр 00;

3) принимаемый кадр 00;

4) принимаемый кадр 00;

5) принимаемый кадр 00;

6) принимаемый кадр 00.

Можно заметить, что 5 и 6 кадры аналогичны, т.е. процесс будет повторяться при приеме каждого очередного кадра, поскольку больше ошибок в принятой комбинации нет. Можно также заметить, что метрика нулевого пути лучше всех остальных. Из примера ясно, что выживающие пути могут отличаться друг от друга в течение долгого времени. Однако в данном примере при приеме 6 кадра первые 4 ребра всех путей совпадают. В этот момент согласно алгоритму Витерби принимается решение о переданных символах, т.к. выжившие пути приходят из одной вершины, т.е. соответствуют оному информационному символу, т.е. по 6 кадру можно с максимальным правдоподобием предположить, что передавалась последовательность 00000000, соответствующая декодированной последовательности 0000.

Выживающие пути могут отличаться друг от друга в течение долгого времени. Однако, в определенный момент согласно алгоритму Витерби принимается решение о переданных символах, т.к. выжившие пути приходят из одной вершины, т.е. соответствуют одному информационному символу.

Номер уровня (столбца) или глубина, на которой осуществляется принятие решения, не может быть вычислена заранее, она является случайной величиной, зависящей от серьезности происходящих в канале ошибок. Поэтому при практической реализации декодера Витерби устанавливается фиксированная глубина декодирования или ширина окна декодирования b. Каждый раз при приеме нового кадра декодер выдает выходящий за пределы окна самый старый символ одного из выживших путей. Такой процесс декодирования кадров продолжается бесконечно. Если b выбрано достаточно большим, то почти всегда при декодировании может быть принято однозначное решение. Если для данного канала с известными параметрами помех код выбран надлежащим образом, то это решение с большой вероятностью будет правильным. Этому, однако, может помешать несколько обстоятельств. Не все выжившие пути могут проходить через один и тот же узел. Возникает неопределенность, и процесс декодирования нарушается. Декодер может разрешить неопределенность, используя любое произвольное правило. Другая возможность состоит в том, что декодер не принимает решения, а отмечает этот участок последовательности, как сегмент кодового слова, который невозможно исправить. В этом случае декодер становится неполным декодером.

Основные трудности при реализации алгоритма Витерби возникают из-за того, что сложность декодера экспоненциально растет с ростом длины кодового ограничения m. Поэтому значения m должны быть сравнительно небольшими m <10 или должны использоваться другие алгоритмы декодирования. Для того, чтобы ослабить влияние больших длин кодового ограничения, была разработана стратегия декодирования, игнорирующая маловероятные пути по решетке, как только они становятся маловероятными. Все такие стратегии поиска наиболее вероятного пути на решетке известны по общим названием последовательного декодирования.

В отличие от декодера Витерби, который производит продолжение и обновление метрики всех путей, которые могут оказаться наилучшими, последовательный декодер в каждый момент времени продолжает лишь один путь, который имеет вид наиболее вероятного. На каждом уровне последовательный декодер находится в одном узле, смотрит на следующий кадр и выбирает ребро, ближайшее к принятому кадру, переходя по этому ребру в узел на следующем уровне. Если нет ошибок, процедура работает отлично, однако при наличии ошибок декодер может выбрать неправильный путь. Если декодер продолжает следовать по ложному пути, он обнаруживает, что происходит слишком много ошибок. Но это ошибки декодера, а не канала. Последовательный декодер вернется назад на несколько кадров и начнет исследовать альтернативные пути до тех пор, пока не найдется правдоподобный путь, затем он будет следовать вдоль этого альтернативного пути. Разработаны различные подробные алгоритмы реализации этих процедур. Наиболее популярным из них является алгоритм Фано.

В этом алгоритме требуется знать вероятность p появления ошибочного символа в канале. Пока декодер следует по правильному пути вероятное число ошибок в первых l кадрах приблизительно равно p ln₀. Декодер допускает несколько большее число ошибок, но если оно намного больше, то декодер сделает вывод о том, что он находится на ложном пути. Для декодера выбирается некоторый параметр p¹, такой, что p<p¹<1/2 и определяется т.н. перекошенное расстояние

,

где – расстояние Хэмминга между принятым словом и текущим путем по решетке. Для правильного пути , в связи с чеми возрастает по мере движения. До тех пор, покавозрастает, декодер продолжает движение вперед по решетке. Еслиначинает уменьшаться, то декодер заключает, что в некотором узле он выбрал неправильное решение и возвращается по решетке, проверяя другие пути. Для того чтобы решить, когдауменьшится на недопустимую величину, декодер пользуется переменным порогомТ, который может быть уменьшен или увеличен на величину , называемую приращением порога. На каждом шаге декодер решает, что делать, основываясь на сравнении перекошенного расстояния и текущего значения порогаТ. До тех пор, пока остается выше порога, декодер продолжает двигаться вперед и повышать порог, подсуммируя, так, чтобы он оставался близким к . Еслиопускается ниже порога, то декодер проверяет альтернативные ребра этого кадра, пытаясь найти то ребро, которое находится выше порога. Если он не может этого сделать, то возвращается назад. Алгоритм заставляет декодер двигаться назад до тех пор, пока он не найдет альтернативный путь, который находится над текущим значением порога, или, если это невозможно, не найдет узел, в котором был установлен текущий порог и понизит его на. Затем декодер снова начнет двигаться вперед с уже пониженным порогом и порог не будет повышаться до тех пор, пока декодер не придет в новый, ранее не исследованный узел решетки. Таким образом, каждый раз, когда декодер, двигаясь вперед, посещает ранее исследованный узел, он имеет меньший порог. Декодер никогда не посетит один и тот же узел дважды с одним и тем же порогом. Следовательно, он может посещать любой узел конечное число раз. Это поведение гарантирует декодер от зацикливания. Декодер продолжает обработку данных, проводя правильное или неправильное декодирование.

Основная сложность при реализации последовательного декодера состоит в том, что число вычислительных операций, необходимых для продвижения в следующую вершину кодового дерева, является случайной величиной. Наиболее существенным следствием непостоянства объема вычислений, требуемых для декодирования одного символа, является необходимость в наличии большой емкости памяти для буферизации поступающих и обрабатываемых данных. Использование в последовательном декодере буферной памяти любого, но конечного объема, приводит к ненулевой вероятности его переполнения. Исходя их этой характеристики, находится т.н. вычислительная скорость декодера R₀ . Если скорость кода R>R₀ , то в любом последовательном декодере будут возникать серьезные вычислительные трудности, связанные с частыми переполнениями буфера.

Для декодирования сверточных кодов могут использоваться и методы синдромного декодирования, среди которых наиболее часто употребляемыми являются метод порогового декодирования и метод табличного поиска. Следует отметить, что синдромное декодирование в преобладающем большинстве случаев используется только для систематических сверточных кодов, т.е. таких, у которых кодовая последовательность содержит явно выделяемые информационные и контрольные символы.

Пороговое декодирование сверточных кодов основано на тех же принципах, что и мажоритарное декодирование блоковых кодов. Декодер, реализующий этот алгоритм, по принятой информационной последовательности вычислят проверочные символы. Для этого декодер содержит копию кодера. Далее полученные с помощью этой копии проверочные символы складываются по модулю два с принимаемой проверочной последовательностью, в результате чего формируется синдромная последовательность, записываемая в регистр сдвига. С помощью линейного преобразования синдрома формируется система ортогональных проверок. Если результаты этих проверок подать на входы пороговой или решающей схемы, то на ее выходе будет формироваться оценка ошибочного символа. Суммируя его по модулю два с соответствующим информационным символом, который хранится в копии кодера, можно исправить ошибку. При этом выходной символ пороговой схемы по цепи обратной связи подается еще и на схему вычисления синдрома и корректирует его, устраняя влияние вычисленной ошибки на последующие символы. Такая процедура порогового декодирования называется декодированием с обратной связью.

Если шумы в канале не выходят за пределы допустимых, то исправление ошибок осуществляется правильно. Если шумы превышают корректирующие способности кода, то могут возникнуть естественные ошибки декодирования. Однако, поскольку декодер содержит цепь обратной связи, то при возникновении ошибки декодирования по неправильной оценке значений ошибок осуществляется неправильная коррекция синдрома, что может привести к новой ошибке декодирования. Это явление характерно для сверточных кодов и известно под названием распространения ошибок.

Одним из методов борьбы с распространением ошибок является т.н. метод дефинитного декодирования. При этом декодировании исправления синдрома не производится, т.е. обратная связь отсутствует. Однако при таком декодировании и достаточно больших кодовых ограничениях корректирующие способности кодов обычно оказываются хуже, чем при декодировании с обратной связью.

Отличие метода табличного поиска от метода порогового декодирования с обратной связью состоит только в том, что в качестве решающего устройства используется ПЗУ с произвольным доступом, из которого по адресу, равному текущему синдрому, выбирается наиболее вероятная комбинация ошибок, записанная в него на этапе проектирования системы.