Нелинейных уравнений Краткие сведения

Рассматриваемые ниже методы относятся к алгебраическим и трансцендентным уравнениям, а также к уравнениям, содержащим нелинейные функции, например, показательную, логарифмическую и т.д.

Алгебраическое уравнение

имеет корней. В общем случае коэффициентымогут быть действительными и комплексными; здесь используется случай действительных коэффициентов.

Трансцендентные уравнения имеют бесконечное множество корней, например, уравнение , которое содержит периодическую тригонометрическую функцию.

Процесс вычисления корней нелинейных уравнений состоит из двух этапов:

1) отделение корней, т.е. установление возможно более тесных промежутков , в которых содержится один и только один корень уравнения

2) уточнение отделенных корней, т.е. доведение значений корней до заданной степени точности.

Отделение корней

Для отделения корней можно воспользоваться методом линейного поиска, в котором диапазон поиска проходится с шагомпри выполнении условия принимается решение о наличии корня в промежутке . В общем случае в диапазоне поиска может оказаться несколько корней (), к каждому из которых следует применить операцию уточнения. Иллюстрация и алгоритм отделения корней представлены соответственно на рис.1.1 и 1.2 приложения.

Уточнение корней

Существует несколько основных методов уточнения корней уравнений.

1 Метод деления пополам (метод дихотомии, метод бисекций)

Это наиболее надежный алгоритм, особенно когда о поведении известно только, что- функция действительной переменнойx и известен интервал ,на которомменяет знак (рис.1.3). Следовательно, междуисуществует точка, в которой функция обращается в нуль. Если разделить интервал пополам и узнать, больше

Рис.1.1 – иллюстрация к отделению корней

нуля или меньше нуля функция в точке деления, то можем указать подынтервал, в котором функция меняет знак. Последующим делением указываемых подынтервалов можно сколь угодно близко подойти к корню: например, за 10 шагов интервал с корнем будет уменьшен в 1024 раза. При заданной абсолютной точности  алгоритм метода деления пополам состоит из следующих шагов (рис.1.4)

1. Вычислить и.Затраты машинного времени на уточнение корня оценивают косвенно, по количеству обращений к функции-, следовательно,будет инкрементирован дважды.

2. Если знаки ине совпадают, т.е. , и, то нужно заменить на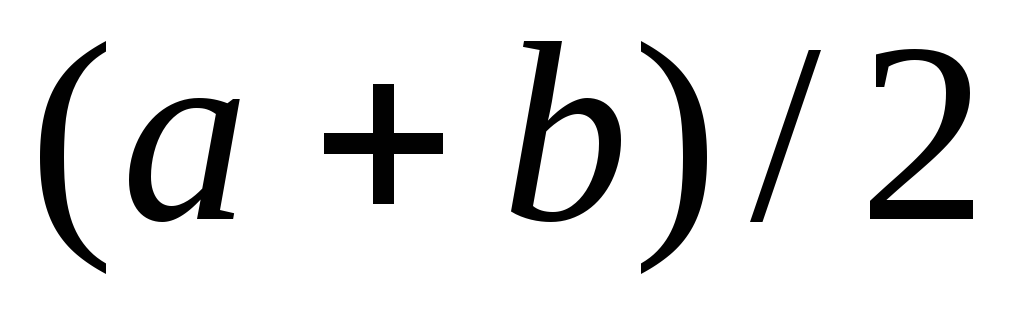и перейти к п.1.

3. Если же при , следует прекратить вычисления, т.к. достигнута заданная точность.

4. Если ,и, то нужно заменитьнаи перейти к п.1; в противном случае - прекратить вычисления, так как достигнута заданная точность. Любой из концов отрезка, а лучше его серединаможет быть использована в качестве корняуравнения.

Отметим основные достоинства метода деления пополам: 1) абсолютно надежен; 2) скорость сходимости не зависит от вида .

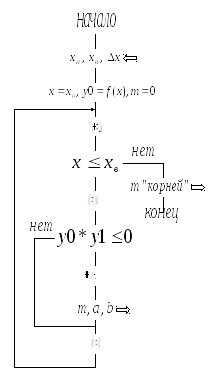
Рис.1.2 – алгоритм отделения корней

2 Метод хорд

Метод деления пополам будет улучшен, если для следующего вычисления использовать не середину отрезка , а то значение в котором дает нуль линейная интерполяция между двумя известными значениями функции противоположного знака (рис.1.5).

Геометрически способ линейной интерполяции эквивалентен замене кривой хордой, проходящей через точки и

Рис.1.3а,б – иллюстрации к методу деления пополам

Уравнение хорды:

Полагая иполучаем приближение к корню:

 (1)

Алгоритм метода хорд (рис.1.6):

1. Вычислить 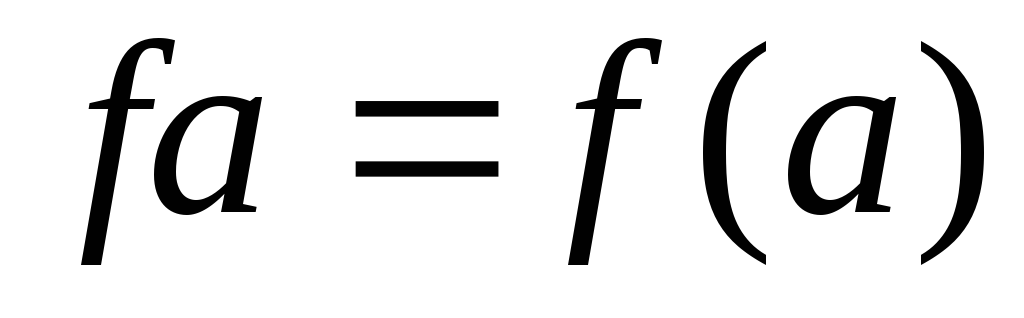и

2. Вычислить по формуле (1) и

3. Если знаки исовпадают, т.е. то конецнеподвижен. В этом случае приняты:если.Затем перейти к п.2. В противном случае, т.е. при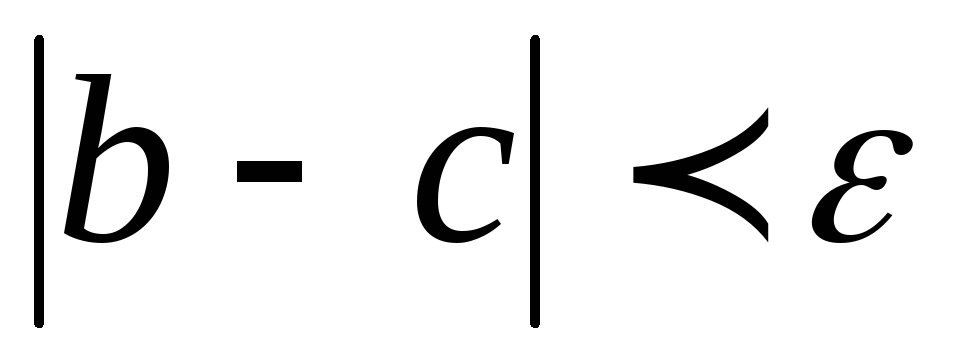вычисления завершены, т.к. заданная точность достигнута.

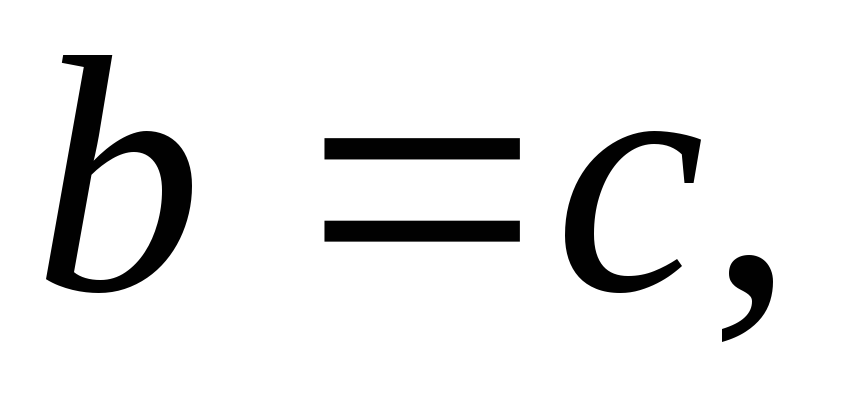
4. Если неподвижен конец. В случае: 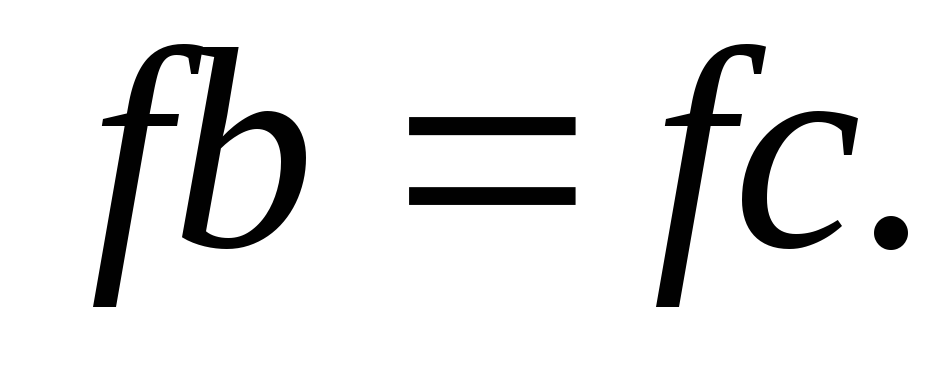Затем перейти к п.2. Иначе – вычисления завершены. Значениеиспользуется как корень уравнения.

Достоинства метода хорд: 1) абсолютно надежен; 2) в большинстве случаев имеет более быструю сходимость, чем метод деления пополам.

Недостаток: скорость сходимости зависит от вида , и поэтому для некоторых функций число шагов на уточнение корня может оказаться большим, чем в методе деления пополам.

Рис.1.4 – алгоритм метода деления пополам