Активный и пассивный двухполюсник

Познакомимся с понятием двухполюсника, которым довольно широко пользуются в теории электрических цепей.

В любой электрической схеме всегда можно выделить какую-то одну ветвь, а всю остальную часть схемы, вне зависимости от её структуры и сложности, условно изобразить некоторым прямоугольником.

Так, в схеме рис. 35 выделим ветвь с резистором R₄, расположенным между узлами «b» и «а» (рис. 36).

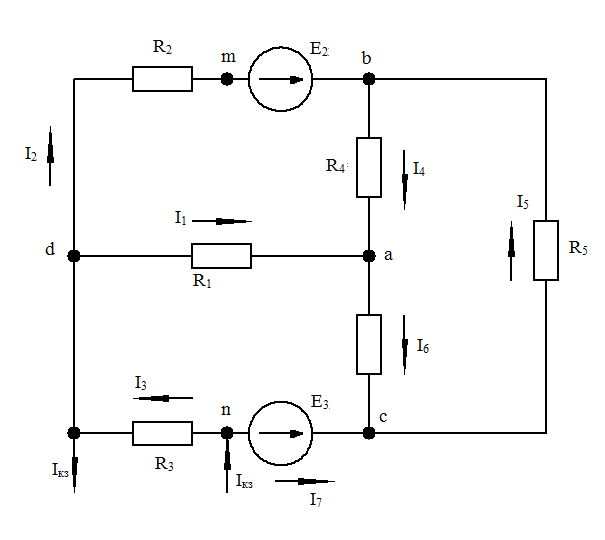
Рис. 35. Схема электрической цепи

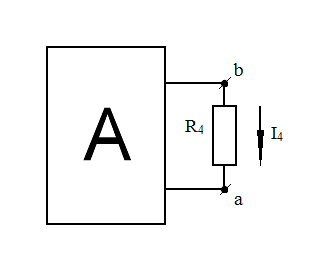
Рис. 36. Схема ативного двухполюсника

По отношению к выделенной ветви вся схема, обозначенная прямоугольником, представляет двухполюсник.

Таким образом, двухполюсник – это обобщенное название схемы, которая своими двумя выходными зажимами (полюсами) присоединяется к выделенной ветви.

Если в составе двухполюсника есть источники ЭДС или тока, то такой двухполюсник называется активным. В этом случае на прямоугольнике ставится буква А (первая буква слова активный).

Если в составе двухполюсника нет источников ЭДС или тока, то такой двухполюсник называется пассивным. В этом случае на прямоугольнике либо не ставится никакой буквы, либо ставится буква П (первая буква слова пассивный)

Метод активного двухполюсника и эквивалентного генератора

В том случае, когда необходимо определить ток в какой-либо ветви без определения токов в остальных ветвях, применяется метод активного двухполюсника и эквивалентного генератора.

Пусть в схеме рис. 36 необходимо определить только ток I₃. Третья ветвь с зажимами d и n выделяется, а вся остальная схема представляется в виде активного двухполюсника рис. 37.

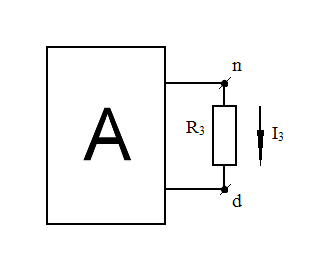
Рис. 37. Схема активного двухполюсника

Активный двухполюсник может быть заменён эквивалентным генератором с ЭДС Е_эг равной напряжению холостого хода U_ххnd на зажимах разомкнутой выделенной ветви nd, а внутреннее сопротивление эквивалентного генератора R_вн равно входному сопротивлению пассивного двухполюсника R_вхnd относительно зажимов n и d выделенной ветви.

Тогда схема рис. 37 принимает следующий вид (рис. 38)

Рис. 38. Схема после замены активного двухполюсника эквивалентным генератором

Тогда ток I₃ выделенной ветви определяется по формуле

I₃= (144)

Следует отметить, что направление холостого хода берётся в направлении тока выделенной ветви в исходной схеме.

Так, на схеме рис. 38 ток I₃ протекает от узла n к узлу d. В этом направлении и берётся разность потенциалов φ_n – φ_d разомкнутой выделенной ветви

φ_n – φ_d = U_ххnd

Далее на практике поступают следующим образом: осуществляют режим холостого хода выделенной ветви, для чего в выделенную ветвь вводится разомкнутый ключ, либо вообще резистор, в данном случае резистор R₃, отбрасывается. Получается новая схема, в которой будет другое токораспределение.

Изобразим схему в режиме холостого хода выделенной ветви nd (рис. 39)

Не обязательно вычислять все токи в схеме рис. 39. Достаточно рассчитать токи I₁` и I<sub>6</sub>`.

По схеме рис. 39 и производится расчёт напряжения холостого хода U_ххnd, т. е. ЭДС эквивалентного генератора.

Рис. 39. Схема в режиме холостого хода выделенной ветви nd

Обозначим на схеме рис. 39 путь, по которому замыкается ток от источника тока I_к, штриховой линией.

В схеме рис. 39 два независимых контура abd и abc. Выберем произвольно направление контурных токов, например, по часовой стрелке.

Составим систему из двух уравнений по методу контурных токов :

I₁₁(R₁ + R₂ + R₄) - I₂₂R₄ + I_КЗR₁ = E₂;

-I₁₁R₄ + I₂₂(R₄ + R₅ + R₆) + I_КЗR₆ = 0; (145)

Здесь (R₁ + R₂ + R₄) – суммарное сопротивление первого контура;

(R₄ + R₅ + R₆) – суммарное сопротивление второго контура. I_КЗR₁ и I_КЗR₆ взяты положительными, потому что контурные токи и тока от источника тока I_КЗ на этих резисторах R₁ и R₆ совпадают.

В правой части Е₂ – суммарная ЭДС первого контура. Во втором контуре ЭДС нет, поэтому в правой части ноль.

Взаимное сопротивление R₄ взято отрицательным, потому что контурные токи I₁₁ и I₂₂, которые используем для расчёта токов I₁` и I<sub>6</sub>`.

I₁`= -I₁₁ - I_КЗ; (146)

I₆`= I₂₂ + I_КЗ; (147)

Направления токов I₁₁ и I_кз противоположны направлению тока I₁`, поэтому в выражении (146) они отрицательны.

Направления токов I₂₂ и I_кз совпадают с направлением тока I₆`, поэтому в выражении (147) они положительные.

Теперь можно определить напряжение холостого хода U_ххnd:

U_ххnd = -I₁`R<sub>1</sub> + I<sub>6</sub>`R₆ – Е₃ (148)

Подсчёт начинаем с точки d. Далее движемся к точке а в сторону убывания потенциала. Поэтому первое слагаемое I₁`R<sub>1</sub> будет отрицательным. Далее движемся от точки а к точке с против тока I<sub>6</sub>`, т.е. в сторону повышения потенциала. Поэтому слагаемое I₆`R₆ будет положительным. На участке cn движемся против ЭДС Е₃, т.е. происходит скачок потенциала на -Е₃.

Входное сопротивление R_вхnd можно определить по схеме пассивного двухполюсника. Для этого в схем рис. 39 идеальные источники ЭДС Е₂ и Е₃ закоротим, потому что внутреннее сопротивление идеальных источников ЭДС равно нулю, а идеального источника тока равно бесконечности. Если в схеме реальные источники ЭДС и тока, то на их месте в схеме пассивного двухполюсника должны оставаться их внутренние сопротивления.

По заданию источника ЭДС и тока идеальные, поэтому схема пассивного двухполюсника будет выглядеть (рис. 40). На этой схеме ет последовательных или параллельных резисторов. Схема сложная, поэтому необходимо произвести преобразование треугольника в звезду или звезды в треугольник.

Преобразуем треугольник резисторов R₄, R₅, R₆ в эквивалентную звезду.

В схеме на рис. 40 обозначена эквивалентная звезда штрихованными линиями.

Рис. 40. Схема пассивного двухполюсника

Изобразим теперь преобразованную схему на рис. 41.

Рис. 41. Преобразованная схема

Теперь на схеме рис. 41 видно отчётливо, что резисторы R₂ и R₄₅ соединены последовательно. Так же последовательно соединены резисторы R₁ и R₄₆. Обе независимые ветви соединены параллельно. Если к этому сопротивлению двух параллельных ветвей включить резистор R₅₆, то это и будет входное сопротивление R_вхnd:

R_вхnd= + R₅₆ (149)

И далее рассчитываем ток I₃ в выделенной ветви nd по формуле (144).

Так производится расчёт в случае, когда параметры схемы известны.

Когда параметры схемы неизвестны, то напряжение холостого хода определяется экспериментальным путём. На зажимах n и d выделенной ветви включается вольтметр. Резистор R₃ отбрасывается (рис. 42):

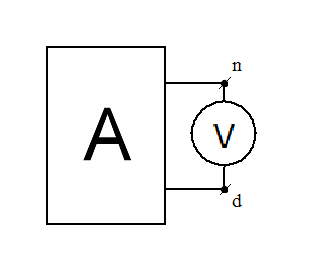
Рис. 42. Схема определения напряжения холостого хода

Вольтметр в схеме рис. 42 определяет напряжение холостого хода U_ххnd.

Если между зажимами n и d включить амперметр, то будет осуществлён режим короткого замыкания ветви ndc (рис. 43).

Рис. 43. Схема определения тока короткого замыкания

Амперметр в схеме рис. 43 замерит ток короткого замыкания I_3К выделенной ветви nd.

Если в схеме рис. 38 закоротить зажимы n и d, то получается схема рис. 44.

Рис. 44. Режим короткого замыкания выделенной ветви

Из схемы рис. 44 получаем:

R_вн =R_вхnd = (150)

Таким образом, показание вольтметра в опыте холостого хода делим на показание амперметра в опыте короткого замыкания и получаем R_вхnd, т.е. входное сопротивление пассивного двухполюсника относительно зажимов выделенной ветви. Оно же внутреннее сопротивление эквивалентного генератора.

Благодаря тому, что использованы режимы холостого хода и короткого замыкания данный метод имеет ещё несколько названий, а именно: метод холостого хода и короткого замыкания, метод эквивалентного генератора, метод активного двухполюсника.

В данном примере рассмотрен самый сложный случай, когда требуется определить ток в выделенной ветви с резистором, к которому подсоединяется источник тока.

Остальные случаи проще. Так, если в схеме рис. 35 требуется найти тока в выделенных ветвях dc, ba, ac, cb, то никаких затруднений не предвидится. Просто изображаете схемы в режиме холостого хода, отбрасывая резисторы R₁, либо R₄, либо R₆, либо R₅. И по этим схемам ищется напряжение холостого хода.

Чуть труднее случай, когда в выделенной ветви есть источник ЭДС. Если в схеме рис. 35 требуется определить ток I₂, то неопытный студент отбрасывает не только резистор R₂ но и источник ЭДС Е₂ при определении напряжения холостого хода. То есть он пытается найти U_ххdb. Расчёт будет неправильный, так как будет потеряна ЭДС Е₂ при определении напряжения холостого хода.

Обязательно нужно ввести точку m между резисторами R₂ источником ЭДС Е₂ и определять напряжение холостого хода U_ххdm. Тогда ЭДС Е₂ не будет потеряна.

Рис. 45. Схема в режиме холостого хода выделенной ветви dm

I₁₁(R₁ + R₃ + R₆) - I₂₂R₆ + I_КЗR₃ = -E₃;

-I₁₁R₆ + I₂₂(R₄ + R₅ + R₆) = 0; (151)

Необходимые токи I₁` и I<sub>4</sub>` будут равны:

I₁`= I₁₁; (152)

I₄`= -I₂₂; (153)

Напряжение холостого хода U_ххdm:

U_ххdm = Е₂ – I₄`R<sub>4</sub> + I<sub>1</sub>`R₁ (154)

Как видим из (154) ЭДС Е₂ не потеряна, она учитывается при расчёте U_ххdm.

8