
5 Том Теория отраслевых рынков / v5-07_gabsz_p160-178
.pdf
170 Ж. Яскольд Габжевич, Ж.-Ф. Тиссе
p2 (s1 , s2 ) = (s2 − s1 ) |
d(4 − s1 − s2 ) − c |
|
||
|
||||
|
|
|
3 |
|
ïðè c/ d < 4 − s1 − s2 è |
|
|
|
|
p1 (s1 , s2 ) = (s2 - s1 )[d(s1 + s2 - 2) + c], |
||||
p2 (s1 , s2 ) = 0 |
|
|
||
ïðè c/ d ³ 4 - s1 - s2.8 |
Åñëè 2d ≤ c, прибыль второго продавца |
|||
P2 [s1 , s2 ; p1 (s1 , s2 ), p2 (s1 |
, s2 )] всегда равна нулю, а прибыль, по- |
|||
лучаемая первым магазином, P1 [s1 , s2 |
; p1 (s1 , s2 ), p2 (s1 , s2 )] — ýòî |
|||
убывающая функция аргумента s1 |
при любом значении s2 |
|||
â SII. Следовательно, для любого s2 S II ïàðà [(s1 , p1 ), (s2 , p2 )] = |
||||
= ({1, (s2 - 1)[d(s2 - 1) + c]}, (s2 , 0)) — ситуация совершенного |
||||
равновесия, при условии 2d ≤ c. |
|
|
||
Åñëè æå 2d > c, то продавец 2 всегда может выбрать s2 достаточно большим, чтобы выполнялось условие c/ d < 4 − s1 − s2, гарантирующее ему строго положительную прибыль. Прибыль же первого продавца все так же понижается с ростом s1 для любого s2 S II, поэтому для продавца 1 максимизация прибыли достигается при s1 = 1.
Положение s2 , доставляющее максимум прибыли второму продавцу, определяется из необходимого условия экстрему ма
dP2 [1, s2 ; p1 (1, s2 ), p2 (1, s2 )] ds2 = 0, ò. å. s2 = (2d - c/ 3d) + 1 è
это строго больше 1, так как 2d > c. Следовательно, если 2d > c,
òî ïàðà |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æì |
(2d |
- c) é |
(2d - c) |
ùü |
|
||
[(s1 |
, p1 ), (s2 |
, p2 )] = |
1, |
|
|
4d + |
|
|
+ c |
, |
|
|
|
|
|
çí |
|
ê |
3 |
|
úý |
|
|
|
|
|
|
èî |
9d ë |
|
ûþ |
|
|||
ì |
(2d |
- c) |
|
(2d - c) é |
(2d - c) |
ùüö |
||
í1 + |
|
|
, |
|
ê2d - |
|
|
- cúý÷ |
3d |
|
3 |
|
|||||
î |
|
9d ë |
|
ûþø |
||||
является единственной ситуацией совершенного равновеси я в этой двухшаговой игре.
8 Ïðè c/ d ³ 4 - s1 - s2 продавец 1 в положении равновесия использует стратегию, подобную стратегии монополиста, преп ятствующую входу на рынок. Действительно, p1 — это та максимальная цена для продавца 1, которая гарантирует ему, что продавец 2 не войдет на рынок даже с нулевой ценой.

О природе конкуренции при дифференциации продукта |
171 |
|
|
Таким образом, при вертикальной дифференциации продукта всегда существует равновесная цена и местоположен ие. В некоторых случаях (2d ≤ c) только одна фирма имеет строго положительную прибыль при равновесии. В остальных же слу- чаях совершенное равновесие дает единственное эндогенн ое решение для цен и продуктовых отличий.9
III. Выводы
Рассмотренные выше примеры показали, что большей стабильности ценовой и продуктовой конкуренции следует ожи - дать при вертикальной дифференциации продукта, чем при горизонтальной. Однако верно ли это в общем случае? Для это го нам необходимо определить обобщенное свойство не-сущест вования равновесной цены в случае горизонтальной дифферен - циации, и наоборот, свойство существования равновесия в о б- щем случае при вертикальной дифференциации. Безусловно, это трудновыполнимая задача (если она выполнима вообще), поэтому будем считать, что рассмотренные нами два примера указывают нам лишь правильный путь рассмотрения этой проблемы.
Одним из шагов на этом пути является некоторое обобщение функции транспортных затрат. А именно давайте предпол о- жим, что транспортные затраты между s è s′ задаются функцией t аргумента s − s′ , которая дважды непрерывно дифференцируема, возрастающая и выпуклая.10 При решении вопроса существования обычно используют теоремы о неподвижной точке, условия которых выполняются при квазивогнутости функции прибыли фирмы. В теории олигополии необходимым
9 В другой статье (Gabszewicz, Thisse 1979) мы рассмотрели модель, перекликающуюся с нынешним исследованием. Две фирмы предполагают продавать взаимозаменяемые продукты потре бителям с одинаковыми вкусами, но различными доходами; идентичнос ть вкусов, влекущая за собой то, что все потребители одинаково ра нжируют товары, ведет к структуре предпочтений, аналогичной мо дели II (вертикальная дифференциация). Описание совершенного ра вновесия в этой модели дано в работе Шайкеда и Саттона (1982).
10 Выпуклость функции t вытекает из вогнутости функции полезности.

172 Ж. Яскольд Габжевич, Ж.-Ф. Тиссе
условием квазивогнутости функции прибыли является вогн у- тость функции спроса. В нашей задаче видно, что свойства функции спроса самым тесным образом связаны с функцией t. Следовательно, проблема существования ценового равнове сия может быть решена путем определения того класса функций транспортных затрат, которые обеспечивают вогнутость фу нкции спроса. Понятно, что результаты будут разными для моделей I и II.
Обозначим через x(p1 , p2 ) положение того покупателя, которому безразлично, у какого продавца приобретать товар. Для модели I x находится как решение уравнения:
p1 + t (x − s1 ) = p2 + t (x − s2 ) , а для модели II x соответственно:
p1 + t (s1 − x ) = p2 + t (s2 − x ) .
Для начала рассмотрим модель I. Предполагая, что x находится между s1 è s2 , с помощью несложных вычислений можно показать, что11
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
t′′( |
|
|
− s1 ) − t′′(s2 − |
|
) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
= − |
x |
x |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
[ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′( |
|
|
− |
|
) + |
|
′( |
− |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dp |
|
|
s1 |
t |
x |
)] |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
t |
x |
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Так как спрос для фирмы 1 — это μ1 (p1 |
, p2 ) = |
|
|
(p1 , p2 ), òî |
||||||||||||||||||||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
вогнутость величины μ1 |
в точке |
|
p1 |
|
эквивалентна вогнутости |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
в точке p1 |
. À |
äëÿ |
этого |
должно |
выполняться условие |
||||||||||||||||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
d2 |
|
|
/ dp12 |
|
≤ 0 для любой цены |
p1. Пусть цена |
|
2 |
— фиксиро- |
|||||||||||||||||||||||||||||||||||||||||||||
x |
p |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t (s1 , s2 ). Тогда |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
+ t (s1 , s2 ) |
|||||||||||||||
âàíà è |
ïðè |
ýòîì |
|
|
p2 > |
äëÿ |
|
p2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
p1 = |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мы получаем |
|
|
|
, p2 ) = s1 , à äëÿ |
|
|
|
p2 |
|
− t (s1 , s2 ) |
получает- |
|||||||||||||||||||||||||||||||||||||||||||
x(p1 |
|
p1 = |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ñÿ x(p1 , p2 ) = s2 . Следовательно, должно выполняться следу- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ющее равенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
|
= − |
d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
′ |
|
|
|
|
|
2 |
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dp1 |
|
(p1 , p2 ) |
|
|
dp1 |
|
(p1 , p2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
11 Заметим, что x может не иметь производных в некоторых ценовых областях; тогда имеет смысл рассматривать право- и л евосторонние производные.
О природе конкуренции при дифференциации продукта |
173 |
|
|
Это означает, что, если только d2 |
|
/ dp12 |
не равняется нулю на |
|||||
x |
||||||||
′ |
′′ |
2 |
|
|
2 |
|||
|
|
|||||||
], величина d x/ dp1 должна менять свой |
||||||||
всем промежутке [p1 |
, p1 |
|||||||
знак на этом промежутке, поэтому x не может быть вогнутой функцией в точке p1.
Перейдем ко второй модели. Получаем
d2 |
|
|
t′′(s1 − |
|
) − t′′(s2 − |
|
) |
|
|||||||||
x |
= |
x |
x |
. |
|||||||||||||
2 |
[ |
′( |
− |
|
|
) − |
|
′( |
− |
|
|
3 |
|||||
|
|
|
|
|
|
||||||||||||
dp |
|
x |
t |
x |
)] |
|
|||||||||||
1 |
|
t |
s1 |
|
|
|
s2 |
|
|
|
|
||||||
Аналогично предыдущему случаю получаем, что вогнутость функции спроса i-й фирмы в точке p1 зависит от вогнутости x в той же точке. Но в отличие от модели I d2 x/ dp12 может быть отрицательной для всех цен p1. Для этого необходимо, чтобы функция t′′ была невозрастающей функцией расстояния, а это достигается тогда, когда функция транспортных з а- трат не «слишком» выпукла.
При изменении моделей I и II с учетом обобщенных функций транспортных затрат мы можем сделать следующие выводы. Во-первых, вогнутость функции спроса почти никогда не имеет места в модели I. Конечно, вогнутость — это только необходимое условие существования ценового равновесия. Но, как мы видели в первом примере, очень часто оно является и достаточным. Как следствие всего этого, равновесие в моде ли I является большой проблемой. В противоположность этому в модели II мы выделили целый класс функций транспортных затрат, обеспечивающих вогнутость спроса, а следовате льно, и существование ценового равновесия. Конечно, это еще н е говорит о наличии совершенного равновесия, но как минимум дает некоторую надежду на устойчивость в модели II.12
12 Отметим, что другие модели подтверждают наши результаты. Так, для общей модели горизонтальной дифференциации п родукта Маклеод (1985) показал, что ценового равновесия не суще - ствует, когда фирмы размещены достаточно близко друг к др угу и предельные производственные затраты убывают с ростом вы пуска. Кроме того, Габжевич доказал существование ценового равновесия в модели вертикальной дифференциации для целого кл асса функций полезности.

174 |
Ж. Яскольд Габжевич, Ж.-Ф. Тиссе |
|
|
ПРИЛОЖЕНИЕ
Утверждение 1.
В модели I не существует ценового равновесия, когда
æ |
1 |
|
|
c |
ö |
|
|
2a £ m inç |
3 |
, |
|
|
|
÷ . |
(À1) |
2 |
d + |
|
|||||
è |
|
c ø |
|
||||
Доказательство.
Пусть (p1 , p2 ) — это равновесные цены. Здесь возникают три ситуации. Так, (p1 , p2 ) может принадлежать такой ценовой области:
D1 = {(p1, p2 ); 1/ 2 - a £ x(p1, p2 ) £ 1/ 2 + a}.
Тогда в D1 x(p1, p2 ) будет равно
p2 - p1 + 2ad + c
4ad + 2c
è
|
|
|
|
|
|
P1 (p1, p2 ) = |
p1 |
p2 - p1 + 2ad + c |
, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4ad + 2c |
|
|
|
|
||||||
|
|
|
|
|
|
P2 (p1, p2 ) = |
p2 |
p1 - p2 + 2ad + c |
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4ad + 2c |
|
|
|
|
||||||
Несложные вычисления приводят к результату p1 = p2 |
= 2ad + c è |
||||||||||||||||||||||||
P1 |
(p1 , p2 ) = ad + c 2 . Для данной цены p2 найдем наилучший ответ |
||||||||||||||||||||||||
|
|
1 |
фирмы 1 на нее в таких областях: |
|
|
|
|
||||||||||||||||||
|
p |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
D11 = {p1; 0 £ |
|
(p1, p2 ) < 1 2 - a}, |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||
ïðè ýòîì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(p1, p2 ) = |
p2 - p1 + 2ad + 2ac |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4ad |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
è |
|
|
|
|
D12 = {p1; 1/ 2 + a < |
|
( p1, p2 ) £ 1} . |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||
Здесь соответственно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
(p1, p2 ) = |
|
p2 - p1 + 2ad - 2ac |
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4ad |
|
|
|
|
|||||
|
|
|
Рассмотрим сначала случай D11. Максимум выражения p1 |
|
(p1 , |
p2 ) |
|||||||||||||||||||
|
|
|
x |
||||||||||||||||||||||
на интервале [0, ¥) достигается в точке p1 = 2ad + ac + c |
2 . Ïðè ýòîì |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
% |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íå |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
видно, что x(p1, |
p2 ) > 1 2 - a. Из этого следует, что в области D11 |
||||||||||||||||||||||||

О природе конкуренции при дифференциации продукта |
175 |
|
|
существует лучшего ответа на цену p2 для фирмы 1. Перейдем к рассмотрению области D12. При данном условии (А1) легко проверить, что максимум P1 (p1, p2 ) в этой области достигается при цене p1 , для которой x(p1, p2 ) = 1, èëè p1 = c(1 − 2a). Учитывая условие (А1),
получаем P1 (p1, p2 ) > P1 (p1 , p2 ). Òàê êàê D1 не содержит равновесной ситуации, то перейдем к рассмотрению второго случая, т . е. си-
туации когда (p1 , p2 ) принадлежит такой ценовой области:
D2 = {(p1, p2 );
Äëÿ D2 имеем
x(p1, p) =
è
P1 (p1, p2 ) =
P2 (p1, p2 ) =
1/ 2 + a < x(p1, p2 ) ≤ 1} .
p2 − p1 + 2ad − 2ac
|
|
4ad |
|
||
p1 |
p2 − p1 |
+ 2ad − 2ac |
, |
||
|
|
||||
|
|
4ad |
|||
p2 |
p1 − p2 |
+ 2ad + 2ac |
. |
||
|
|
||||
|
|
4ad |
|||
Легко показать, что решения p1 è p2 необходимых условий экстре-
ìóìà (dP1 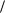 dp1 = 0 è dP2
dp1 = 0 è dP2 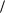 dp2 = 0 ) имеют вид x( p1, p2 ) > 1 2 + a. Таким образом, (p1 , p2 ) не принадлежит внутренности области D2 , поэтому
dp2 = 0 ) имеют вид x( p1, p2 ) > 1 2 + a. Таким образом, (p1 , p2 ) не принадлежит внутренности области D2 , поэтому
должно быть верно x(p1 , p2 ) = 1. Но тогда p2 не является лучшим ответом фирмы 2 против цены p1, òàê êàê P2 (p1 , p2 ) = 0 . Следовательно, в области D2 у нас не существует ценового равновесия.
Рассмотрим последний случай:
( p1 , p2 ) D3 = {(p1, p2 ); 0 ≤ x(p1, p2 ) < 1 2 − a}.
2 − a}.
Аналогично предыдущим рассуждениям легко показать, что и в этом случае равновесия не существует.
Утверждение 2.
В модели II существует единственная точка равновесия, опре деляемая формулами:
p1 (s1, s2 ) |
= (s2 |
− s1 ) |
d(s1 + s2 + 2) + c |
, |
|
|
|
||||
|
|
3 |
|
|
|
p2 (s1, s2 ) |
= (s2 |
− s1 ) |
d(4 − s1 − s2 ) − c |
|
, |
|
|||||
|
|
3 |
|
|
|
176 |
|
|
Ж. Яскольд Габжевич, Ж.-Ф. Тиссе |
|
|
|
|
|
|
когда |
|
|
|
|
|
c |
|
< 4 - s1 - s2 , |
(À2) |
|
d |
|||
|
|
|
||
è |
|
|
|
|
p1 (s1, s2 ) = (s2 - s1 )[d(s1 + s2 - 2) + c] , |
|
|||
p2 (s1 , s2 ) = 0 , |
|
|
||
когда |
|
|
|
|
|
c |
|
³ 4 - s1 - s2 . |
(À3) |
|
d |
|||
|
|
|
||
Доказательство.
Пусть (p1 , p2 ) — ситуация равновесия. (Так как функция прибыли квазивогнута, мы знаем, что такое равновесие существ ует.) Предположим, что верно условие (А2). Тогда на области
D1 = {(p1, p2 ); m1 (p1, p2 ) > 0 è m2 (p1, p2 ) > 0}
функции спроса для фирм задаются формулами:
m1 (p1, p2 ) = |
p2 - p1 + c(s2 - s1 ) + d(s22 - s12 ) |
|
|
|||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2d(s2 - s1 ) |
||||||
è |
p1 - p2 + 2d(s2 - s1 ) - c(s2 - s1 ) - d(s22 - s12 ) |
|
||||||||||
m2 (p1, p2 ) = |
. |
|||||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2d(s2 - s1 ) |
||||||
Åñëè (p1 , p2 ) Î D1 , òî p1 è p2 |
должны удовлетворять необходи- |
|||||||||||
мым условиям экстремума: |
|
|
|
|
|
|
|
|||||
|
|
|
dPi |
|
= 0 , |
|
i = 1, 2. |
|||||
|
|
|
dpi |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
Соответственно |
|
|
|
|
|
|
|
|
|
|
|
|
p1 (s1, s2 ) = (s2 |
- s1 ) |
d(s1 + s2 + 2) + c |
|
|||||||||
|
|
|||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
||
è |
|
|
|
|
|
|
|
|
|
|
|
|
p2 (s1, s2 ) = (s2 |
- s1 ) |
d(4 - s1 - s2 ) - c |
. |
|||||||||
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
И если верно условие (А2), то p2 > 0 è (p1 , p2 ) Î D1. Тогда для доказательства того, что найденные выше цены будут действител ьно рав-

О природе конкуренции при дифференциации продукта |
177 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
новесными, достаточно показать, что P |
(p , |
p ) > |
P |
( |
|
|
, p ), ãäå |
|
|
— |
p |
i |
p |
i |
|||||||
i |
i |
j |
i |
|
|
j |
|
|
||
это наилучший ответ фирмы i против цены |
p в области |
|
|
|
||||||
|
|
j |
|
|
|
|
|
|
|
|
Di = {pi ; μ j (pi, pj ) = 0}.
Пусть i = 1. Тогда
pi = 2 3 (s2 − s1 )[d(s1 + s2 − 1) + c].
Используя условие (А2) получаем, что P1 (p1 , p2 ) > P1 (p1, p2 ). Тогда (p1 , p2 ) D1 — это ситуация равновесия.
Пусть теперь верно условие (А3). Тогда из всего вышесказанн о- го следует, что (p1 , p2 ) должно принадлежать множеству
D2 = {(p1, p2 ); μ1 (p1, p2 ) = 1}.
Òî, ÷òî p2 равно нулю, следует из того факта, что фирма 2 за счет понижения цены может захватить некоторую долю рынка. Пуст ь
p1L = (s2 − s1 )[d(s1 + s2 − 2) + c] —
это решение уравнения для μ1 ( p1, 0) = 1. ßñíî, ÷òî p1L доминирует над любой другой ценой, p1 < p1L . Кроме того, можно показать, что dP1 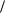 dp1 < 0 для любой цены p1 > p1L при условии (А3). Следовательно, мы имеем p1 = p1L .
dp1 < 0 для любой цены p1 > p1L при условии (А3). Следовательно, мы имеем p1 = p1L .
Литература
1.Bertrand J. Théorie mathématique de la richesse sociale // Journal des Savant. 1883. Vol. 48. P. 499–508.
2.d’Aspremont C., Jaskold Gabszewicz J., Thisse J.-F. On Hotelling’s stability in competition // Econometrica. 1979. Vol. 47. P. 1145– 1150.
3.Eaton B. C., Lipsey R. G. Freedom of entry and the existence of pure profits // Economic Journal. 1978. Vol. 88. P. 455–469.
4.Edgeworth F. The pure theory of monopoly // Â êí.: Papers Relating to Political Economy. London : Macmillan, 1925. Vol. 1. P. 111– 142.
5.Hotelling H. Stability in competition // Economic Journal. 1929. Vol. 39. P. 41–57.
6.Jaskold Gabszewicz J., Thisse J.-F. Price competition, quality and income
disparities // Journal of Economic Theory. 1979. Vol. 20. P. 340– 359.
178 |
Ж. Яскольд Габжевич, Ж.-Ф. Тиссе |
|
|
7.Jaskold Gabszewicz J., Shaked A., Sutton J., Thisse J.-F. Price competition among differentiated products: a detailed study of Nash equilibrium // London School of Economics. ICERD DP 8137. 1981.
8.Lancaster K. Variety, Equity and Efficiency. New York : Columbia
University Press, 1979.
9.MacLeod W. B. On the non-existence of equilibria in differentiated product models // Regional Science and Urban Economics. 1985. Vol. 15. P. 245–262.
10.Selten R. Re-examination of the perfectness concept for equilibrium points in extensive games // International Journal of Game Theory. 1975. Vol. 4. P. 25–55.
11.Shaked A., Sutton J. Relaxing price competition through product differentiation // Review of Economic Studies. 1982. Vol. 69. P. 3–13.
12.Shaked A., Sutton J. Product differentiation and industrial structure // London School of Economics. ICERD DP 85113. 1985.
