Организация операционного блока магистрального операционного устройства
Тип операционного блока (ОПБ) определяется способом обработки данных. Раз-
личают ОПБ последовательного и параллельного типа.
В последовательном операционном блоке (рис. 7.7) операции выполняются по-
битово, разряд за разрядом.
Рис. 7,7. Последовательный операционный блок
Бит переноса, возникающий при обработке 1-го разряда операндов, подается на вход ОПБ и учитывается при обработке (i+1)-го разряда операндов. Результат
побитово заносится в выходной регистр, предыдущее содержимое которого перед
этим сдвигается па один разряд. Таким образом, после n циклов в выходном регистре формируется слово результата, где каждый разряд занимает предназначенную для него позицию.
При параллельной организации операционного блока (рис. 7.8) всё разряды операндов обрабатываются одновременно. Внутренние переносы обеспечиваются схемой ОПБ. Более подробно возможности организации переносов рассматриваются
позже.
Рис. 7.8. Параллельный операционный блок
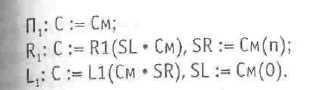
Микрооперация Пi обеспечивает передачу результата на магистраль С без сдвига. Пo ходу микрооперации R, результат сдвигается на один разряд вправо, при этом в освобождающийся старший разряд заносится значение с внешнего контакта SL, а выдвигаемый (младший) разряд сумматора посылается внешний контакт 5R.
В микрооперации L, результат сдвигается на один разряд влево. Здесь в осво-
бождающийся младший разряд заносится значение с внешнего контакта SR, а вы-
двигаемый (старший) разряд См передается на внешний контакт SL.
Базис целочисленных операционных устройств
Для большинства современных ВМ общепринятым является такой формат с фик-сированной запятой (ФЗ), когда запятая фиксируется справа от младшего разряда кода числа. По этой причине соответствующие операционные устройства называют целочисленными ОПУ. В форме с ФЗ могут быть представлены как числа без знака, когда все n позиций числа отводятся под значащие цифры, так и со знаком. В последнем случае старшим (n-1)-й разряд числа занимает знак числа (0 —плюс, 1 — минус), а под значащие цифры отведены разряды с (n- 2)-го по 0-й.
При записи отрицательных чисел используется дополнительный код, который для
числа N получается по следующей формуле:
Если исключить логические операции, которые рассматриваются отдельно, це-
лочисленное ОПУ должно обеспечивать выполиепне следующих арифметических
операций над числами без знака и со знаком:
- сложение/вычитание;
- умножение;
- деление.
Сложение и вычитание
На рис. 7.10 приводятся примеры сложения целых чисел, представленных в до-
полнительном коде (напомним, что при сложении в дополнительном коде знако-
вый разряд участвует в операции наравне с цифровыми).
Рис. 7,10. Примеры выполнения операции сложения в дополнительном коде:
а, б, в, г — сложение без возникновения переполнения;
д, е — сложение с переполнением
При сложении-разрядных двоичных чисел (бит знака и n-1 значащих цифр)
возможен результат, содержащий n значащих цифр. Эта ситуация известна как
переполнение. «Лишний» бит занимает позицию знака, что приводит к некорректности результата. Естественно, что ОПУ должно обнаруживать факт перопсцш *'
иия и сигнализировать о нем. Для этого используется следующее правило: ее»-
суммируются два числа и они оба- положительные или оба отрицательные, Пеп
полиеиие имеет место тогда и только тогда, когда знак результата протшюпол,
жен знаку слагаемых. Рисунки 7.10,3 и 7.10, е показывают примеры перелол1Ге
ния, Обратим внимание, что переполнение не всегда сопровождается переносов
из знакового разряда.
Рис. 7.11. Примеры выполнения операции вычитаний в дополнительном коде: а, б, s, г —
вычитание без возникновения переполнения; д, е — вычитание с переполнением J
Вычитание выполняется в соответствии с правилом: для вычитания одного числа (вычитаемого) из другого (уменьшаемого) необходимо взять дополнение вычитаемого и прибавить его к уменьшаемому. Под дополнением здесь понимается вычитаемое с противоположным знаком, представленное в дополнительном коде.
Вычитание иллюстрируется примерами (рис. 7.11). Два последних примера (см. рис. 7.11,д и 7.11,е) демонстрируют ранее рассмотренное правило обнаружения
переполнения.
Чтобы упростить обнаружение ситуации переполнения, часто применяется так
называемый модифицированный дополнительный код, когда для хранения знака
отводятся два разряда, причем оба участвуют в арифметической операции наравне с цифровыми разрядами. В нормальной ситуации оба знаковых разрядах содержат одинаковые значения. Различие в содержимом знаковых разрядов служит признаком возникшего переполнения (рис. 7.12).
Рис. 7.12. Примеры выполнения операции сложения в модифицированном дополнительном коде: а, б — переполнения нет; в,г — возникло переполнение
На рис. 7.13 показана возможная структура операционного блока для сложения и вычитания чисел со знаком в формате с фиксированной запятой. Центральным звеном устройства является n-разрядный двоичный сумматор. Операнд А поступает на вход сумматора без изменений. Операнд В предварительно пропускается через схемы сложения по модулю 2, поэтому вид кода В, поступающего на другой вход сумматора, зависит от выполняемой операции. Если задана операция сложения (управляющий код 0, то результат на выходе ОПБ определяется выражением S=A+B. При операции вычитания (управляющий код 1) на вход сумматора подаются инверсные значения всех разрядов В, и, кроме того, на вход переноса в младший разряд сумматора СIN поступает 1. В итоге на выходе ОПБ будет S= A + B + 1,что соответствует прибавлению к А числа В с противоположным знаком, то есть
вычитанию.
Рис. 7.13. Структура операционного блока для сложения и вычитания
На рис. 7.13 не показана схема формирования признака переполнения V, кото-
рый согласно описанным ранее правилам определяется логическим выражением
