Сравнительная оценка схем умножения с матричной и древообразной структурой

В табл. 7.4 приведены данные по производительности различных видов умножи­телей, выполненных средствами интегральной схемотехники. Быстродействие умножителей характеризуется коэффициентом при величине задержки _l в одном Логическом элементе.

Таблица 7.4. Сравнение производительности умножителей в интегральном исполнении

Содержимое таблицы плюс некоторые не включенные в нее данные позволяет сделать следующие выводы. Наиболее быстро работают умножители, построеные по схеме Бута, а также имеющие древовидную структуру, в частности дерево Дадда. Для операндов длиной в 16 разрядов и более наиболее привлекательной представляется модифицированная схема Бута, как по скорости, так и по затратам оборудования. Максимально быстрое выполнение операции умножения обеспечивает сочетание алгоритма Бута и дерева Уоллеса. С другой стороны, достаточно хорошие показатели скорости при умножении чисел небольшой разрядности выдает схема Бо-Вули. В плане потребляемой мощности наиболее экономичными являются умножители, построенные по схемам Брауна и Пезариса. Несмотря на сравнительно небольшое число используемых транзисторов, схемы на базе алгоритма Бута, а также древовидные реализации, потребляют больше из-за избыточ­ных внутренних связей, связанных с нерегулярной структурой этих схем.

Конвейеризация параллельных умножителей

В матричной и древовидной структурах параллельных умножителей заложен еще один потенциал повышения производительности — возможность конвейеризации. При конвейеризации весь процесс вычислений разбивается на последовательность законченных шагов. Каждый из этапов процедуры умножения выполняется на сво­ей ступени конвейера, причем все ступени работают параллельно. Результаты, по­лученные на i-ой ступени, передаются на дальнейшую обработку в (i + 1)-ю сту­пень конвейера. Перенос информации со ступени на ступень происходит через буферную память, размещаемую между ними (рис. 7.43).

Рис. 7.43. Структура конвейерного умножителя

Выполнившая свою операцию ступень помещает результат в буферную нам и может приступать к обработке следующей порции данных операций, в то время как очередная ступень конвейера в качестве исходных использует данные, хранящиеся в буферной памяти на ее входе. Синхронность работы конвейера обеспечивается тактовыми импульсами, период которых определяется самой медленной ступенью конвейера и задержкой в элементе буферной памяти …Несмотря на то что время выполнения операции умножения для каждой конкретной пары сомножителей в конвейерном умножителе не только не уменьшается, но даже несколько увеличивается за счет задержек в буферной памяти при последовательном перемножении последовательностей пар сомножителей, достигаемый выигрыш весьма ощутим. Действительно, в конвейерном умножителе из k ступеней перемножаемые данные могут подаваться на вход с интервалом в k раз меньшим, чем в случае обычного умножителя. В том же темпе появляются и ре­зультаты на выходе,

Схема конвейера легко может быть применена к матричным и древовидным умножителям. В матричных умножителях в качестве ступени конвейера выступа­ет каждая строка матрицы сумматоров. В качестве примера конвейеризированно­го матричного умножителя на рис. 7.44 приведена схема 4x4. Черными прямо­угольниками обозначены триггеры-защелки, образующие буферную память.

Рис. 7.44. Конвейеризированный матричный умножитель

Конвейеризация матричных умножителей на уровне строк сумматоров может быть затруднительной из-за большого числа ступеней и необходимости введения в состав умножителя значительного количества триггеров-защелок. Сокращение числа триггеров достигается за счет следующих приемов;

- отказа от использования идеи конвейеризации между входными схемами «И» и первой строкой полных сумматоров;

- увеличением времени обработки на каждой ступени, например можно принять его равным удвоенному времени срабатывания полного сумматора;

- отказом от формирования всех п² битов частичных произведений в самом начале, перед первой ступенью конвейера, и вычислением их по мере необходимости стало на разных ступенях конвейера.

В древовидных умножителях в качестве ступеней конвейера выступают каскады сжатия, то есть более крупные образования, чем в матричных умножителях. Кроме того, количество каскадов компрессии также значительно меньше. Это делает конвейеризацию древовидных умножителей более привлекательной. На рис. 7.45 показана точечная диаграмма конвейеризированного умножителя со схемой Дадда.

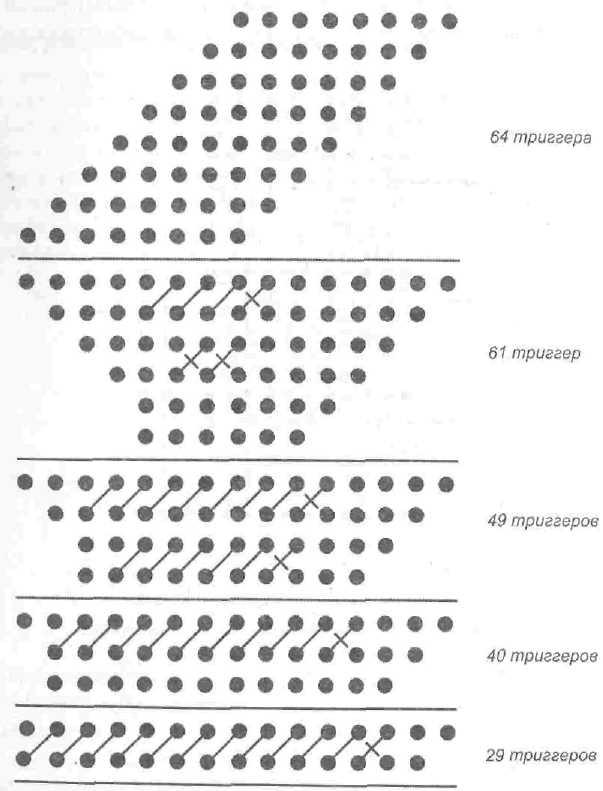
Рис. 7.45. Древовидный конвейеризированный умножитель со схемой Дадда

В правой части рисунка указано количество триггеров-защелок, необходимых каждой ступени конвейера. Как видно, в умножителе Дадда 8x8 требуются 243 триггера, не считая дополнительных триггеров для конвейеризации последнего этапа сложения частичных произведений. Количество триггеров может быть сокращено за счет увеличения времени, выделяемого на выполнение операций ступени конвейера. Это позволяет убрать некоторые из триггеров.

При конвейеризации умножителя на базе дерева Уоллеса требуется меньше триггеров-защелок, поскольку в этой схеме основное сжатие суммы частичных произведений происходит на более ранних этапах. Кроме того, для заключитель­ного суммирования векторов сумм и переносов используется более «короткий» сумматор.