Алгоритм Бо-Вули

Несколько иная схема матричного умножителя, также обеспечивающего умноже­ние чисел в дополнительном коде, была предложена Бо и Були [61]. В алгоритме Бо-Вули произведение чисел в дополнительном коде представляется следующим соотношением:

Матрица умножения, реализующая алгоритм, приведена на рис. 7.31, а соответствующая ей схема умножителя — на рис. 7.32. . '

По ходу умножения частичные произведения, имеющие знак «минус», смещаются к последней ступени суммирования. Недостатком схемы можно считать то, что на последних этапах работы требуются дополнительные сумматоры, из-за чего регулярность схемы нарушается.

Рис. 7.31. Матрица перемножения n-разрядных чисел согласно алгоритму Бо-Вули

Рис. 7.32. Матричный умножитель для четырехразрядных чисел в дополнительном коде по схеме Бо-Вули

Алгоритм Пезариса

Еще один алгоритм для вычисления произведения чисел в дополнительном коде был предложен Пезарисом [181].

При представлении числа в дополнительном коде старший разряд числа имеет отрицательный вес. Для учета этого обстоятельства Пезарис выдвигает идею использовать в умножителе четыре вида полных сумматоров (рис. 7.33).

Рис. 7.33. Виды сумматоров, применяемых в матричном умножителе Пезариса

В сумматоре типа СМО, который фактически является обычным полным сумматором. все входные данные (x, у, z) имеют положительный вес, а результат лежит в диапазоне 0-3. Этот результат представлен двухразрядным двоичным числом cs, где с и s также присвоены положительные веса. В остальных трех типах сумматоров некоторые из сигналов имеют отрицательный вес. Схема умножений в рассматриваемом методе показана на рис. 7.34.

Рис. 7-34. Матрица перемножения n-разрядных чисел согласно алгоритму Пезариса

Здесь знак «минус» трактуется следующим образом: -1 = -2 * 1 + 1; -0 = -2 * 0 + 0. Схема умножителя, реализующего алгоритм Пезариса, приведена на рис. 7.35.

По сравнению с умножителем Бо-Вули, схема Пезариса имеет более регуляр­ный вид, но, с другой стороны, она предполагает присутствие нескольких типов сумматоров.

Древовидные умножители

Сократить задержку, свойственную матричным умножителям, удается в схемах, построенных по древовидной структуре. Если в матричных умножителях для cсуммирования п частичных произведений требуется п строк сумматоров, то в древовидных схемах количество ступеней сумматоров пропорционально Iog₂n (рис. 7.3(3)-Соответственно числу ступеней суммирования сокращается и время вычисления СЧП. Хотя древовидные схемы быстрее матричных, однако при их реализации требуются дополнительные связи для объединения разрядов, имеющих одинаковый вес, из-за чего площадь, занимаемая схемой на кристалле микросхемы, может оказаться даже больше, чем в случае матричной организации сумматоров. Еще одна проблема связана с тем, что стандартное двоичное дерево не является самой эффективной древовидной иерархией, поскольку не позволяет в полной мере

Рис. 7.35. Матричный умножитель для четырехразрядных чисел в дополнительном коде по схеме Пезариса

Рис. 7.36. Суммирование частичных произведений в умножителях: а — с матричной структурой; б — со структурой двоичного дерева

воспользоваться возможностями полного сумматора (имеющего не два, а три входа), благодаря чему можно одновременно суммировать сразу три входных бита. По этой причине на практике в умножителях с древовидной структурой применя­ет иные древовидные схемы. С другой стороны, такие схемы не столь регулярны, как двоичное дерево, а регулярность структуры — одно из основных требований при создании интегральных микросхем.

Древовидные умножители включают в себя три ступени:

- ступень формирования битов частичных произведений, состоящую из п² эле­ментов «И»;

- ступень сжатия частичных произведений — реализуется в виде дерева параллельных сумматоров (накопителей), служащего для сведения частичных произведений к вектору сумм и вектору переносов. Сжатие реализуется несколькими рядами сумматоров, причем каждый ряд вносит задержку, свойственна одному полному сумматору;

- ступень заключительного суммирования, где осуществляется сложение вектора сумм и вектора переносов с целью получения конечного результата. Обычно здесь применяется быстрый сумматор с временем задержки, пропорциональным O(log₂(n)).

Известные древовидные умножители различаются по способу сокращения числа ЧП. При использовании в умножителе СМ и ПС их обычно называют счетчиками (3,2) и (2,2) соответственно. Связано это с тем, что код на выходах стал, как и в двоичном счетчике, равен количеству единиц, поданных на входы.

Процесс «компрессии» СЧП завершается формированием двух векторов — век­тора сумм и вектора переносов, которые для получения окончательного результа­та обрабатываются многоразрядными сумматорами, то есть различие между древовидными схемами сжатия касается, главным образом, способа формирования упомянутых векторов.

В известных на сегодня умножителях наибольшее распространение получили три древовидных схемы суммирования ЧП: дерево Уоллеса, дерево Дадда и пере­вернутое ступенчатое дерево. В наиболее общей формулировке дерево Уоллеса — это оператор с п входами и log₂n выходами, в котором код на выходе равен числу единиц во входном коде. Вес битов на входе совпадает с весом младшего разряда выходного кода. Простей­шим деревом Уоллеса является СМ. Используя такие сумматоры, а также полу­сумматоры, можно построить дерево Уоллеса для перемножения чисел любой разрядности, при этом количество сумматоров возрастает пропорционально величине \og₂n. В такой же пропорции растет время выполнения операции умножения,. Согласно алгоритму Уоллеса, строки матрицы частичных произведений груп­пируются по три. Полные сумматоры используются для сжатия столбцов с тремя битами, а полусумматоры — столбцов с двумя битами. Строки, не попавшие в набор из трех строк, учитываются в следующем каскаде редукции. Количество строк в матрице (ее высота) на j-й ступени определяется выражениями

В 32-разрядном умножителе на базе дерева Уоллеса высоты матриц ЧП после­довательно уменьшаются в последовательности: 22, 15, 10, 7, 5, 4, 3 и 2. Логика построения дерева Уоллеса для суммирования частичных произведений в умно­жителе 4x4 показана на рис. 7.37, а. Для пояснения структуры дерева сумматоров часто применяют так называемую точечную диаграмму (рис. 7.37, 6). В ней точки обозначают биты частичных произведений, прямые диагональные линии представ­ляют выходы полных сумматоров, а перечеркнутые диагонали — выходы полусумматоров. Хотя на рис. 7.37, а в третьем каскаде показаны три строки, фактически после редукции остаются лишь две первых, а третья лишь отражает переносы, которые учитываются при окончательном суммировании. Этим объясняется кажущиеся отличие от точечной диаграммы.

Рис. 7.37. Суммирование ЧП с помощью дерева Уоллеса (вариант 1): а — логика суммирования; б — точечная диаграмма

Умножитель (рис. 7.38) состоит из трех ступеней с высотами 4,3,2 и содержит 16 схем «И», 3 полусумматора, 5 полных сумматоров. Сложение векторов сумм и переносов в последнем каскаде реализуется четырехразрядным сумматором с последовательным распространением переноса, однако чаще для ускорения привлекаются более эффективные схемы распространения переноса, например параллельная. Отметим, что избыточность кодирования, заложенная в алгоритм Уоллеса, приводит к тому, что возможно построение различных вариантов схемы дерева. Так, LpHc. 7.39 показана иная реализация дерева Уоллеса для четырехразрядных операндов. Как видно, новый вариант схемы никакого выигрыша в аппаратурном плане не дает.

Схема Уоллеса считается наиболее быстрой, но в то же время ее структура наи­менее регулярна, из-за чего предпочтение отдается иным древовидным структу­рам. Основная сфера использования умножителей со схемой Уоллеса — перемно­жение чисел большой разрядности. В этом случае быстродействие имеет превали­рующее значение.

При умножении чисел небольшой разрядности более распространена другая схема сжатия суммирования ЧП — схема дерева Л. Дадда. В ее основе также лежит дерево Уоллеса, но реализуемое минимальным числом сумматоров.

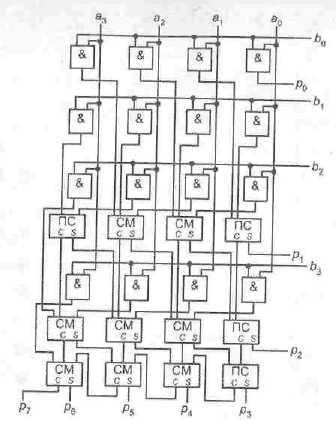
Рис. 7.38. Умножитель 4x4 со структурой дерева Уоллеса

Рис. 7,39. Суммирование ЧП с помощью дерева Уоллеса (вариант 2): а — логика суммирования; б — точечная диаграмма

Схема редукции, предложенная Л. Даддом, начинается с определения высоты промежуточных матриц частичных произведений: , пока dj < п. Значения для dj приведены в табл. 7.3.

Так, 32-разрядный умножитель на базе дерева Дадда имеет высоты промежуточных матриц 29,19,13,9,6,4,3 и 2. На j-й от конца ступени умножителя используетcя минимальное число ПС и СМ, позволяющее сократить число битов в столбце d_j. Если высота столбца, включающая переносы, равна h, то число полусумматоров (N_nc) и полных сумматоров

(N_СМ) составляет:

На рис. 7.40 описан умножитель 4 х 4, реализующий алгоритм дерева Дадда. Для этого требуется 16 схем «И», два полусумматора, четыре полных сумматора и шестиразрядный сумматор. Схема содержит три ступени с высотами промежу­точных матриц: 4,3 и 2. На этапе суммирования вектора сумм и вектора переносов необходим (2п - 2)-разрядный сумматор.

рис. 7.40. Суммирование ЧП с помощью дерева Дадда для случая чисел без знака: а — логика суммирования; б — точечная диаграмма

Схема умножения чисел в дополнительном коде, рассмотренная примени­тельно к матричному умножителю, может быть адаптирована и для умножителя со схемой Дадда. В таком случае схема сжатия приобретает вид, показан­ий на рис. 7.41.

Рис. 7.41. Суммирование ЧП в дополнительном коде с помощью дерева Дадца: а — логика суммирования; б — точечная диаграмма

Различия методов Уоллеса и Дадда являются следствием разных подходов к ре­шению задачи «компрессии» суммирования. Алгоритм Уоллеса ориентированы на сжатие кодов как можно раньше, на самых ранних этапах, а алгоритм Дадда стре­мится это сделать по возможности позже, то есть наибольший уровень сжатия от­носит к завершающим стадиям.

Сравнивая схемы Уоллеса и Дадда, можно отмстить, что число каскадов сжа­тия в них одинаково, однако количество используемых полусумматоров и полных сумматоров в схеме Дадда меньше (при подсчете числа элементов обычно не учи­тывают многоразрядные сумматоры, предназначенные для окончательного сложе­ния векторов сумм и переносов). С другой стороны, на этапе сложения векторов сумм и переносов в варианте Уоллеса требуется сумматор с меньшим числом раз­рядов (в нашем примере — 4 против 6).

У обеих схем имеется общий недостаток — нерегулярность структуры, особенно у дерева Уоллеса.

Схема перевернутой лестницы (overturned stairs), предложенная в [169], являет собой одну из попыток сделать древообразную структуру более регулярной, а значит, облегчить ее реализацию в интегральном исполнении. «Лестница* строится из базовых блоков трех видов (рис. 7.42, я), которые авторы назвали «ветвью» (branch), «соединителем» (connector) и «корнем» (root).

Базовые элементы объединяются, образуя дерево, имеющее п входов. Подобная схема на 18 входов показана на рис. 7.42,6. Как видно, дерево имеет достаточно

Рис. 7.42. Перевернутое дерево: а - базовые блоки; б - структура дерева на 18 входов

регулярную структуру, однако нужно учитывать, что веса отдельных входов различаются. Кроме того, конструкция умножителя получается сложной.