Матричное умножение чисел без знака

Результат Р перемножения двух n-разрядных двоичных целых чисел А и В без зна­ка можно описать выражением

Умножение сводится к параллельному формированию битов из п n-разрядных частичных произведений с последующим их суммированием с помощью матрицы сумматоров, структура которой соответствует приведенной матрице умножения. Схема известна как умножитель Брауна. На рис. 7.28 показан такой умножитель для четырехразрядных двоичных чисел, в котором каждому столбцу в матрице умножения соответствует диагональ умножителя. Биты частичных произведений (ЧП) вида a_ib_j формируются с помощью элементов «И». Для суммирования ЧП Применяются два вида одноразрядных сумматоров с сохранением переноса: полу­сумматоры (ПС)¹ и полные сумматоры (СМ).

----------------------------

1 Полусумматоры называется одноразрядное суммирующее устройство, имеющее дна входа для слагаемыx и два входа и два выхода — выход бита суммы и выход бита переноса.

Рис. 7.28. Матричный умножитель Брауна для четырехразрядных чисел без знака

Матричный умножитель п х п содержит п^г схем «И», ПС и (п² - 2п) СМ.Если принять, что для реализации полусумматора требуются два логических элемента, а для полного сумматора — пять, то общее количество логических элементов в ум­ножителе составляет п² + 2п + 5(п² - 2л) = 6п² – 8n.

Быстродействие умножителя определяется наиболее глинным маршрутом рас­пространения сигнала, который в худшем случае (пунктирная линия на рис. 7.28) включает в себя прохождение одной схемы «И», двух ПС и (2п - 4) СМ. Полагая задержки в схеме «И» и полусумматоре равными Л, а в полном сумматоре — 2Д. общую задержку в умножителе можно оценить выражением {4n - 5)Д. Чтобы со­кратить ее длительность, n-разрядный сумматор с последовательным переносом в нижней строке умножителя можно заменить более быстрым вариантом сумма­тора. Последнее, однако, не всегда желательно, поскольку это увеличивает число ис­пользуемых в умножителе логических элементов и ухудшает регулярность схемы.

В общем случае задержка в матричных умножителях пропорциональна их разрядности: 0(п).

Матричное умножение чисел в дополнительном коде

К сожалению, умножитель Брауна годится только для перемножения чисел знака. При обработке знаковых чисел отрицательные представляются дополнительным кодом, а матричные умножителя строятся по схемам, отличным от схемы Брауна. Прежде всего, напомним, что запись двоичного тела в дополнительном коде (с дополнением до 2) имеет вид '£"

член правого выражения представляет знак числа, а сумма — его модуь.

Исходя из приведенной записи, произведение Р двух n-разрядных двоичных целых чисел А и В в дополнительном коде (значение произведения и сомножителей в дополнительном коде обозначим соответственно V(P), V{A) и V(B)) можно

Матрица умножения чисел со знаком, представленных в дополнительном коде, похожа на матрицу перемножения чисел без знаков (рис. 7.29). Отличие состоит в том, что (2n - 2) частичных произведений инвертированы, а в столбцы п и (2n - 1) добавлены единицы.

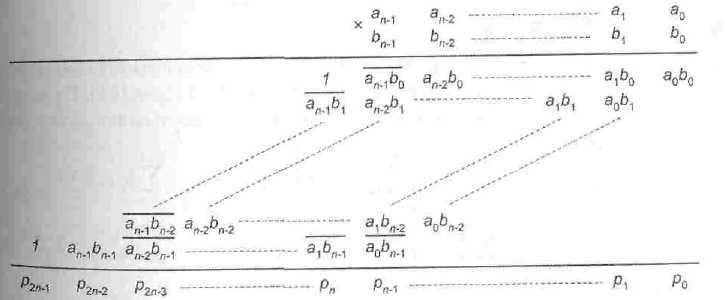
Рис. 7.29. Матрица перемножения n-раэрядных чисел а дополнительном кода

Соответствующая схема матричного умножителя для четырёхразрядных чисел показана на рис. 7.30.

Здесь (2n - 2) частичных произведений инвертированы за счет замены элемен­та «И» на элементы «И-НЕ». Сумматор в младшем разряде нижнего ряда складывает 1 в столбце n с вектором сумм и переносов из предшествующей строки, реализуя при этом следующие выражения:

Инвертор в нижней строке слева обеспечивает добавление единицы, в столбец (2n-1).

Рис. 7.30. Матричный умножитель для четырехразрядных чисел в дополнительном коде