
Глава 2. Построение и анализ модели
2.1 Сбор и предварительная обработка исходной информации
В ходе работы нами была создана выборка, объемом 50 турпакетов. Результаты набора были представлены в таблице (см. ПРИЛОЖЕНИЕ А).
Для расчетов мы будем использовать прикладной программный пакет для эконометрического моделирования Gretl.
Проведем обработку информации по следующему алгоритму:
Вычисление выборочных характеристик;
Отсев грубых погрешностей;
Проверка нормальности распределения
Преобразование распределения к нормальному (при необходимости).
Цифровые метки фиктивных переменных
Большая часть выбранных факторных признаков – качественные. Поэтому для дальнейшего анализа нам необходимо ввести их цифровые обозначения (см. Таблица 1).
Таблица 1 – Цифровые метки фиктивных переменных
|
Признак |
Значение |
Метка |
|
Класс отеля |
2* |
2 |
|
3* |
3 | |
|
4* |
4 | |
|
5* |
5 | |
|
Тип пития в отеле |
BB |
1 |
|
HB |
2 | |
|
FB |
3 | |
|
Категория номера |
std; |
0 |
|
superior |
1 | |
|
suit |
2 | |
|
de luxe |
3 | |
|
studio |
4 | |
|
Расположение отеля относительно моря |
1 линия |
1 |
|
2 линия |
2 | |
|
3 линия |
3 | |
|
Курортная зона |
Санур |
1 |
|
Кута |
2 | |
|
Семиньяк |
3 | |
|
Нуса-Дуа |
4 | |
|
Горящая путевка |
Путевка с вылетом в августе |
0 |
|
Путевка с вылетом в апреле |
1 | |
|
Пляж |
Муниципальный |
0 |
|
Собственный |
1 |
Приступим к выполнению алгоритма.
Вычисление выборочных характеристик (см. Таблица 2).
Таблица 2 – Описательная статистика
|
Переменная |
Среднее |
Медиана |
Ст. откл. |
Вариация |
|
Класс отеля |
3,2000 |
|
0,69985 |
|
|
Тип питания |
1,5200 |
|
0,73512 |
|
|
Пляж |
0,220000 |
|
|
|
|
Курорт |
2,4200 |
|
0,40975 |
|
|
Тип номера |
1,46000 |
|
1,4028 |
|
|
Горящий тур |
0,440000 |
|
0,50143 |
|
|
Цена |
79650,6 |
77243,5 |
21885,5 |
0,274768 |
|
Переменная |
Асимметрия |
Эксцесс |
5% Perc. |
95% Perc. |
|
Цена |
0,219750 |
-1,29288 |
49722,3 |
114940, |
Обратим внимание на значение некоторых коэффициентов.
Медиана и среднее значение цены близки, что может свидетельствовать о распределении, близком к нормальному. Если представить наши данные в виде столбчатой диаграммы (рис. 1), то можно посмотреть соотношение моды, медианы и средней. Медиана находится между модой и средней величиной, причем ближе к средней, чем к моде, это также говорит о том, что распределение по форме близко к нормальному1.
Коэффициент асимметрии показывает незначительную правостороннюю асимметрию, коэффициент эксцесса – то, что график распределения будет «приплюснутым».
Показатель вариации цены 27,4% приемлем для выбранной нами темы.
О распределении значений цены также можно сказать, что 5% выбранных путевок дешевле 49772 руб, а 95% - 114940 руб.
Рисунок 1 – Соотношение моды, медианы и средней

Обратим внимание на значение средней бинарных переменных пляж и горящая путевка, 0,22 и 0,44, соответственно, то есть только 22% отелей из нашей выборки имеют в собственности пляж, и 44% путевок предполагают вылет в апреле. На основании значений можно предположить, что влияние переменной, соответствующей признаку пляж, будет незначимым, а влияние переменной, описывающей время вылета, будет значимым.
Примерно две трети нашей выборки находятся в ценовой области 79650,6± 21885,5 руб.
Отсев грубых погрешностей
Проверим на аномальность наибольшее и наименьшее значения цены турпутевки, используя статистику:2

Вычисления произведем с помощью MS Office Excel.
Для Pmax= 116319,0 τ=|116319 – 79804|/22173=1,675485492.
В качестве критерия, с которым будем сопоставлять расчетное значение τ, выберем τр. Вычислим τр с помощью таблицы критических значений распределения Стьюдента:

Из таблицы распределения Стьюдента выбираем при n=48 и доверительной вероятности (1-p) 95% и 99,9% критические значения t5%=1,6772 и t0,1%=3,2669.
Вычислили и получили τ5%= 1,647007, τ0,1%= 2,985493.
1,647007<τ<2,985493, следовательно значение не признается аномальным и не исключается из выборки.
Проверим на аномальность минимальное значение pmin=42922,0:
τ=1,663374.
При t5%=1,6772, t0,1%=3,2689 статистики равны
τ5%= 1,647007, τ0,1%= 2,985493. Таким образом, τ0,1% >τ> τ5%, что означает отсутствие погрешности.
Проверка распределения на нормальность
Проверка распределения на нормальность – основное содержание предварительной обработки результатов наблюдений.
Сформулируем нуль-гипотезу:
Н0: распределения является нормальным, и альтернативную ей
Н1 : распределение не является нормальным.
Быструю проверку гипотезы нормального распределения проведем с помощью R/S̄ - критерия, где R – размах выборки. Для этого вычислим отношение
R/S̄= (116319- 42922)/ 22173,0=3,310197
Сопоставим полученное значение с критическими границами этого отношения, приведенными в соответствующей таблице, при вероятности ошибки 5%.3
R/S̄ниж=3,83, R/S̄верх=5,35: рассчитанное нами значение не попадает в указанный интервал, следовательно, отвергается гипотеза о нормальном распределении.
Судить о близости распределения к нормальному можно также по значения коэффициентов асимметрии и эксцесса.4
Гипотезу о нормальном распределении не следует отвергать, если
 и
и
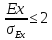 ,
где
,
где


Для нашей выборки As=0,219750, Ex=-1,29288,
σAs =0,336600709, σEx = 0,661908375.
При As/σAs = 1,531743839, Ex/σEx = -0,511964277
 и
и
 ,
следовательно, подтверждается нулевая
гипотеза о нормальном распределении.
,
следовательно, подтверждается нулевая
гипотеза о нормальном распределении.
Далее проведем более строгую проверку распределения с помощью критерия χ2.
