
интегрирование дробно-рациональных функций
.docИнтегрирование рациональных дробей
Рациональной
дробью называется функция
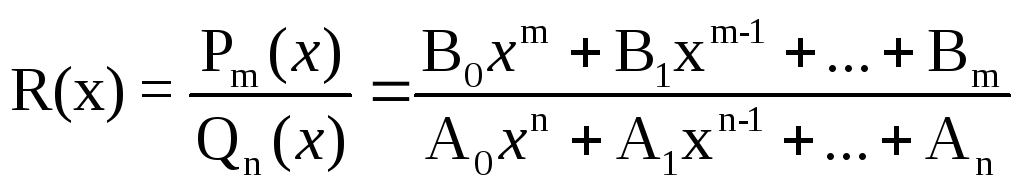 где Bj,
Ai
-заданные коэффициенты,
где Bj,
Ai
-заданные коэффициенты,
![]() ,
,
![]() .
Рациональная дробь называется правильной,
если m<n, неправильной, если mn.
.
Рациональная дробь называется правильной,
если m<n, неправильной, если mn.
Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной дроби.
Действительно,
пусть R(x)=![]() - неправильная рациональная дробь.
Разделим числитель на знаменатель,
получим
- неправильная рациональная дробь.
Разделим числитель на знаменатель,
получим
![]() ,
где Ll(x)
и остаток rk(x)
- многочлены, а
,
где Ll(x)
и остаток rk(x)
- многочлены, а
![]() - правильная рациональная дробь.
- правильная рациональная дробь.
Любой многочлен
![]() может быть представлен в виде:
может быть представлен в виде:
![]()
Где
![]() - корень кратности k1;
- корень кратности k1;
![]() - корень кратности k2;
- корень кратности k2;
![]() - корень кратности kl.
- корень кратности kl.
В таком случае
правильную дробь
![]() можно представить в виде:
можно представить в виде:
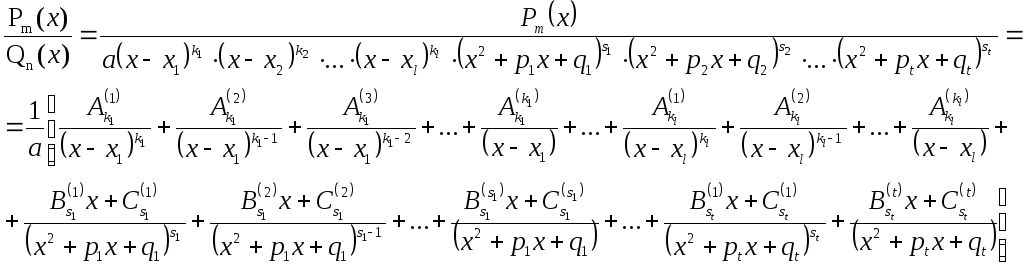
Все дроби представленные в разложении исходной дробно-рациональной функции называются простейшими, числа A, B, C с различными индексами называются неопределенными коэффициентами и однозначно определяются из решения системы линейных уравнений составляемой путем приведения всех простейших дробей к одному знаменателю из соображения однозначности представления многочлена по степеням своей переменной.
В результате представленного разложения становиться возможным вместо взятия интеграла от исходной дробно-рациональной функции (сообразуясь со свойствами неопределенного интеграла) брать интегралы от полученных простейших дробей и в качестве ответа к исходному примеру записывать их линейную комбинацию.
Отметим тот факт,
что получившиеся при разложении
простейшие дроби бывают четырех видов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Приведем вычисление интегралов от этих простейших дробей.
1. ![]() .
.
2. ![]() .
.
3. 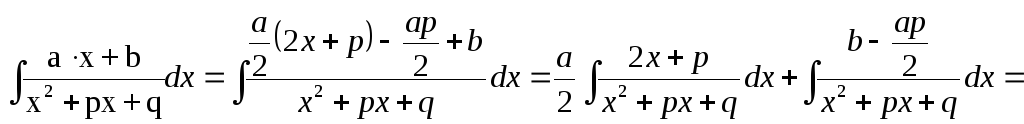
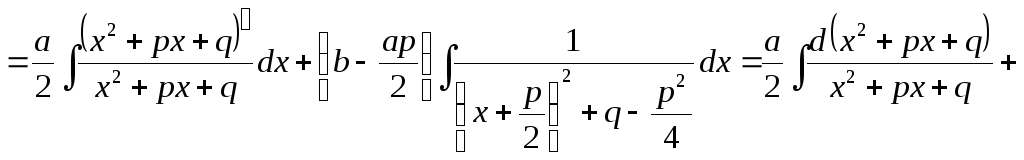
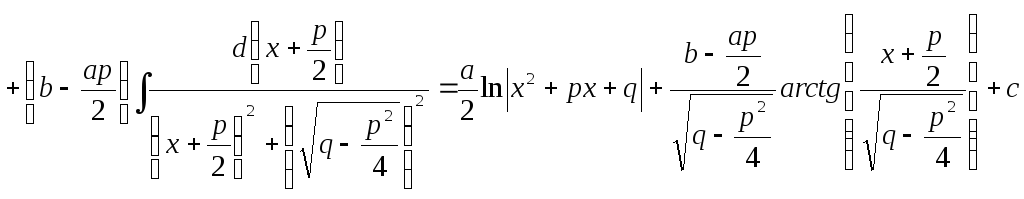
4. 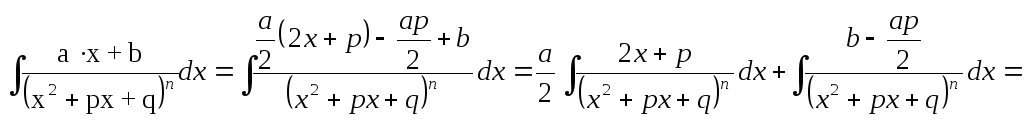
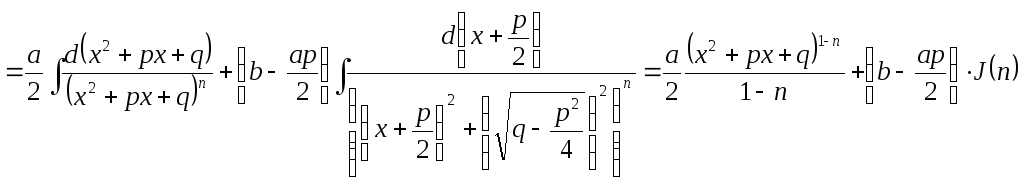
где
![]()
Использовав для
данного интеграла метод интегрирования
по частям можно получить рекуррентную
формулу:
![]() по которой, действуя последовательно,
можно спуститься до
по которой, действуя последовательно,
можно спуститься до
![]() .
.
Таким образом, обобщая все вышесказанное можно сформулировать алгоритм пригодный для интегрирования дробно-рациональных функций.
1. Выделяем целую часть, и получаем интеграл от многочлена и правильной дробно-рациональной функции.
2. Представляем правильную дробно-рациональную функцию как сумму простейших дробей.
3. Вычисляем интегралы от простейших дробей.
4. Записываем ответ как сумму от получившихся в п.3. выражений.
Найти неопределенный
интеграл: ![]()
Данный пример предполагает применение метода вычисления интегралов от дробно-рациональных функций.
Алгоритм наших действий следующий:
1. Выделяем целую
часть, и получаем интеграл от многочлена
и правильной дробно-рациональной
функции.
![]() т.е.
т.е.
![]()
2. Представляем
правильную дробно-рациональную функцию
как сумму простейших дробей.
![]() в силу единственности представления
многочлена получаем систему уравнений:
в силу единственности представления
многочлена получаем систему уравнений:
![]() т.е.
т.е.
![]()
3. Вычисляем интегралы от простейших дробей.
![]()
![]()
![]()
![]()
4. Записываем ответ как сумму от получившихся в третьем пункте выражений.
![]()
