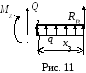
3 Участок (рис. 11): ,1,5 м;
=
-2х3
+1,75;
=
- 1,75х3.
При
1,75
кН,
0, при
1,5
м
-1,25
кН,
-0,375 кНм.
Вычисляем минимальное значение изгибающего момента:
=
0,
0,875
м;
=
-0,766 кН·м.
Построим эпюры поперечной силы и изгибающего момента (рис. 8).
Задание 2 определение геометрических характеристик составного поперечного сечения
Целью задания является определение центра тяжести и вычисление главных центральных моментов инерции составного сечения.
Для заданного составного поперечного сечения стержня, состоящего из равнополочного уголка, прямоугольника и двутавра или швеллера (рис. 12),
1) определить положение центра тяжести относительно первоначально принятых осей;
2) вычислить осевые и центробежный моменты инерции сечения относительно центральных осей, параллельных первоначально принятым осям;
3) определить положение главных центральных осей инерции сечения;
4) вычислить величины главных моментов инерции сечения.
5) сделать чертеж заданного сечения в масштабе и указать на нем основные размеры и оси.
Исходные данные взять из табл. 2. Данные о прокатных профилях принимаются из таблиц сортамента (ГОСТ 8239-72, ГОСТ 8240-72, ГОСТ 8509-86).
Таблица 2
|
№ п/п |
Номер двутавра или швеллера |
Прямоугольник, мм |
Равнополочный уголок, мм |
|
б |
в |
г | |
|
1 |
10 |
20010 |
80806 |
|
2 |
12 |
22012 |
80808 |
|
3 |
14 |
24010 |
75757 |
|
4 |
16 |
24014 |
75758 |
|
5 |
18 |
25014 |
75759 |
|
6 |
20 |
24012 |
70706 |
|
7 |
22 |
22010 |
70707 |
|
8 |
24 |
23012 |
70708 |
|
9 |
27 |
25010 |
707010 |
|
0 |
30 |
30014 |
63636 |
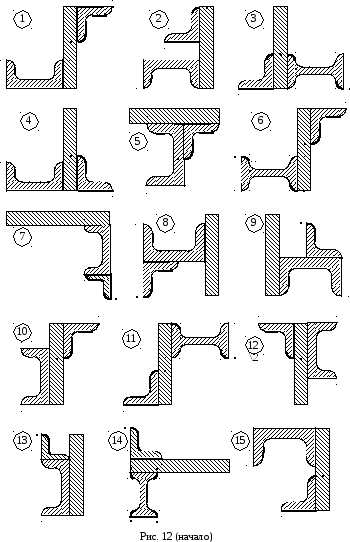
Пример выполнения задания 2
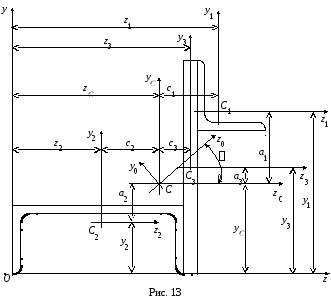
Вычислить главные моменты инерции составного сечения (рис. 13).
Исходные данные: Составное сечение представляет собой набор из трех элементов: равнополочного уголка 63636 мм, швеллера № 16 и прямоугольника 20012 мм.
Решение
1. Выпишем из таблиц сортамента и подсчитаем геометрические характеристики отдельных частей поперечного сечения:
а) равнополочный
уголок 63636
мм (рис. 14):
b1=
6,3 см,
7,28
см2,
27,1
см4,
42,9
см4,
11,2
см4,
1,78 см,
= -45
(поворот главных осей z0
и y0
по часовой стрелке), Iz1y1=
=
sin2
=
sin2(-45)
= -15,85 cм4;
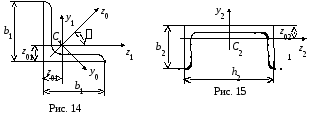
б) швеллер № 16
(рис. 15): h2
= 16 см; b2
= 6,4 см,
18,1
см2,
1,8
см,
747 см4,
63,3
см4,
(оси
z2
и
y2
являются
главными центральными осями);
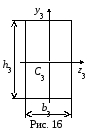
в) прямоугольник 20012 мм (рис. 16):
b3
= 1,2 см, h3
= 20 см,
1,220
= 24 см2,
см4,
=
2,88
см4,
(оси
z3
и
y3
- главные
центральные оси).
2. Проводим вспомогательные оси z и y, заключив все сечение в положительной четверти (рис. 13). Определим координаты центров тяжести О1, О2 и О3 отдельных частей сечения в системе координат zOy:
=
h2
+ b3
+ z01
= 16 + 1,2 + 1,78 = 18,98 см;
=
h2
/2 = 16/2 = 8 см;
= h2
+ b3
/2 = 16 + 1,2/2 = 16,6 см;
= h3
- b1+
z01=20
- 6,3 + 1,78 = 15,48 см;
= b2
-
6,4 – 1,8 = 4,6 см;
= h3/2
= 20/2 = 10 см.
3. Определим координаты центра тяжести заданного сечения в системе координат zОy:
zC
=
=
=
=
=
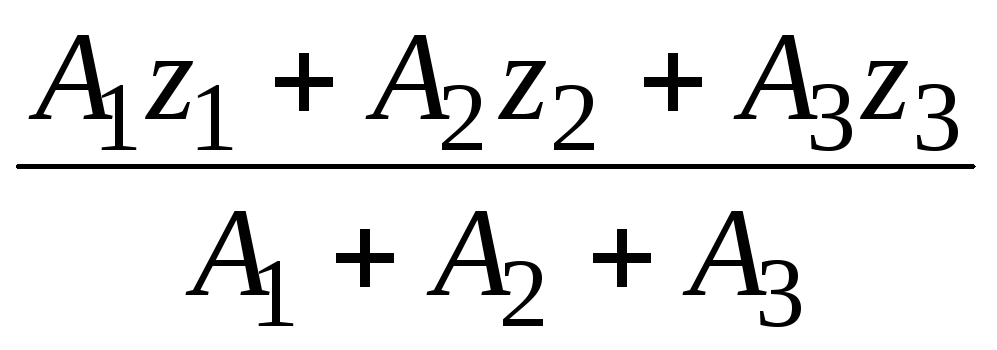см;
yC
=
=
=
= 
=
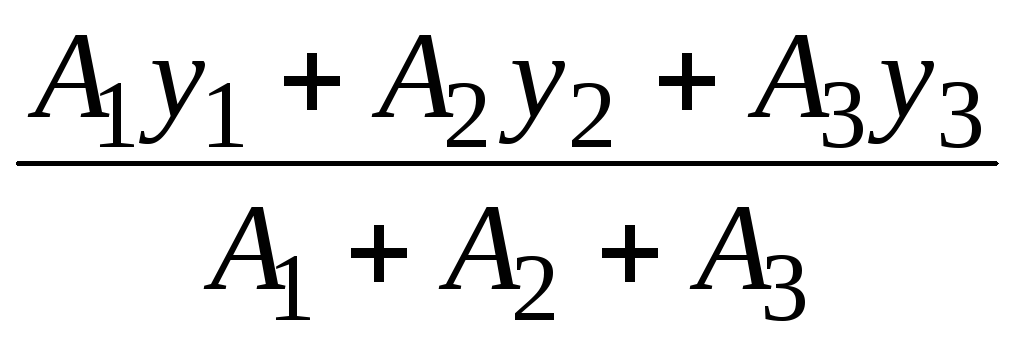см.
Центр тяжести С заданного сечения должен находиться внутри многоугольника, вершинами которого являются центры тяжести отдельных частей сечения, в нашем примере - внутри треугольника C1 C2 C3.
4. Проводим центральные оси zC и yC параллельно осям z и y. Вычисляем расстояния между осями zC и z1, z2, z3, осями yC и y1, y2, y3:
а1 = у1 – уC = 15,48 - 8,83 = 6,65 cм;
a2 = y2 – yC = 4,6 - 8,83 = -4,23 cм;
a3 = y3 – yC = 10 - 8,83 = 1,17 cм;
c1 = z1 – zC = 18,98 - 13,8 = 5,18 cм;
c2 = z2 – zC = 8 - 13,8 = -5,8 cм;
с3 = z3 – zC = 16,6 - 13,8 = 2,8 cм.
5. Вычисляем значения осевых и центробежного моментов инерции заданного сечения относительно центральных осей zC и zC по формулам параллельного преобразования осей:
=
27,1
+ 6,6527,28
+ 63,3 +
+ (-4,23)218,1 + 800 + 1,17224 = 1569,01 см4;
=
27,1 + 5,1827,28
+ 747 +
+ (-5,8)218,1 + 2,88 + 2,8224 = 1769,34 см4;
=
-15,85 + 6,655,187,28
+ + 0 + (-4,23)(-5,8)18,1
+ 0 + 1,172,824
= 757,61 см4.
6. Определим положение главных центральных осей инерции сечения:
tg 20
=
=
=
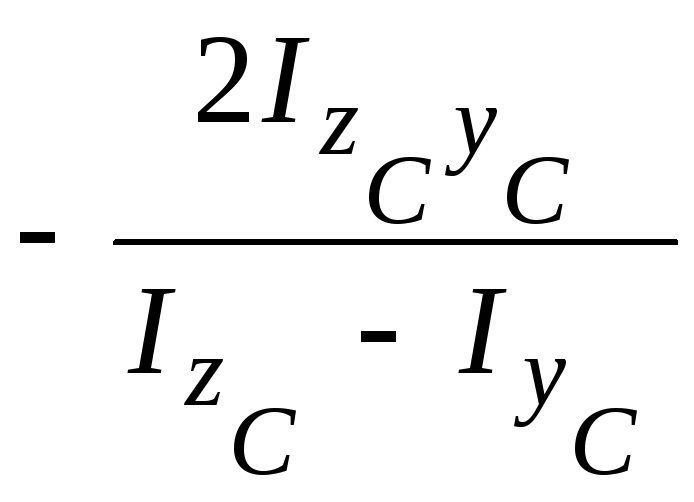7,564,
откуда 0 = 41,23.
Угол 0 положительный, поэтому оси zC и yC поворачиваем против часовой стрелки на угол 41,23 и проводим главные центральные оси сечения z0 и y0 (рис. 13).
7. Вычисляем значения главных центральных моментов инерции сечения по формулам углового преобразования осей:
=
cos20
+
sin20
–
sin20
=
=1569,01 cos241,23 + 1769,34 sin2 41,23 – 757,61 sin(2·41,23) = 904,97 cм4;
=
cos20
+
sin20
+
sin20
=
= 1769,34 cos241,23 + 1569,01 sin241,23 + 757,61sin(2·41,23) = 2433,38 см4.
Значения главных моментов инерции сечения можно вычислять также и по формуле
=
=
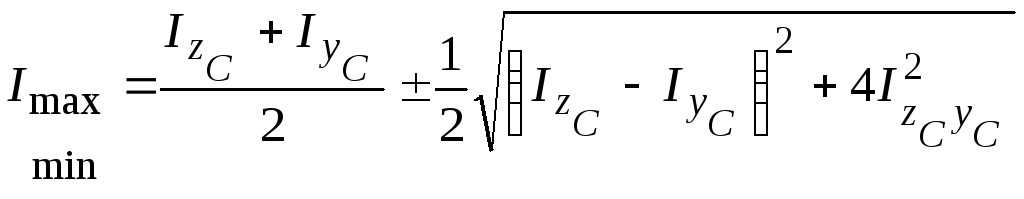1669,17
1528,41;
Imax = 2433,38 см4; Imin = 904,97 см4.
Если центробежный
момент инерции сечения
0, то главная ось инерции, относительно
которой главный момент инерции сечения
принимает максимальное значение,
проходит через четные четверти. Поэтому
=
Imax
= 2433,38
см4;
=
Imin
= 904,97 см4.
Правильность вычислений значений главных моментов инерции сечения проверяем по выполнению условий:
а) сумма моментов инерции сечения относительно двух взаимно перпендикулярных осей при повороте осей не меняется
+
=
+
,
2433,38 + 904,97 = 1569,01 + 1769,34,
3338,35 = 3338,35;
б) центробежный момент инерции сечения относительно главных осей равен нулю
=
sin20
+
cos20
=
=
sin(2·41,23)
+ 757,61
cos(2·41,23)=
-99,30 + 99,30 = 0.
Значит, расчет выполнен точно.