Контрольная №1 для заочниковИЭУП
.docВариант 1
1)
Найти косинус угла между векторами
и
.
2) Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
3)
Компланарны
ли векторы
,
и
?
4) Вычислить
площадь параллелограмма, построенного
на векторах
и
.
5) Найти расстояние
от точки
до плоскости, проходящей через точки
.
6) Написать
уравнение плоскости, проходящей через
точку
перпендикулярно вектору
.
7) Исследовать кривую второго порядка и построить ее.
8) Вычислить.
где
,
.
9) Вычислить
определитель 
10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
11) Найти все значения корня.
12) Найти пределы (не пользуясь правилом Лопиталя)
а)
б)
в)
г)
д)
13) Найти производные
данных функций:
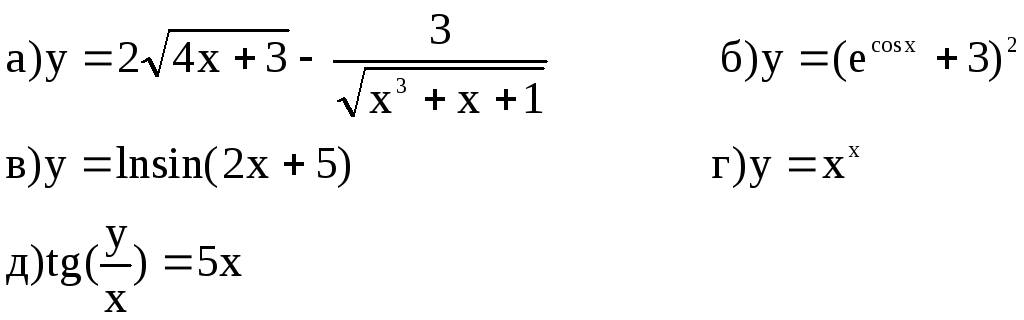
14) Найти
и
а) у = х2ln
x
б)
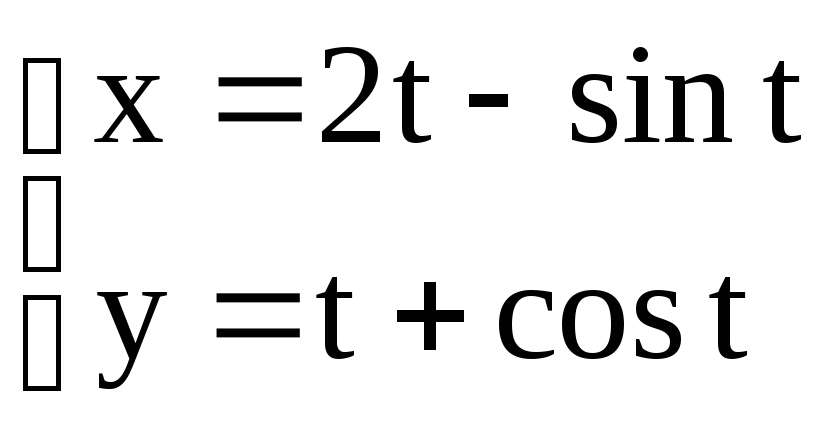
15) Найти производную указанного порядка.
16) Найти пределы пользуясь правилом Лопиталя
а)
б)
17) Найти первые и вторые частные производные
18) Провести полное исследование функции и построить ее график.
Вариант 2
1)
Найти косинус угла между векторами
и
.
2) Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
3) Компланарны
ли векторы
,
и
?
4) Вычислить
площадь параллелограмма, построенного
на векторах
и
.
5) Найти расстояние
от точки
до плоскости, проходящей через точки
.
6) Написать
уравнение плоскости, проходящей через
точку
перпендикулярно вектору
.
7) Исследовать кривую второго порядка и построить ее.
8) Вычислить.
где
,
.
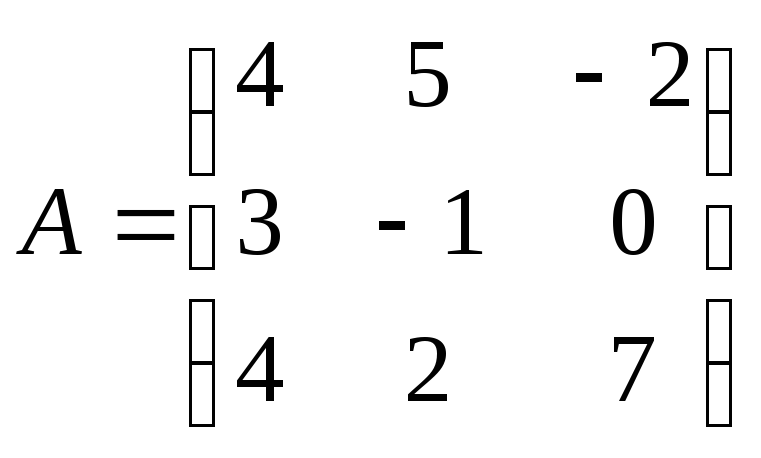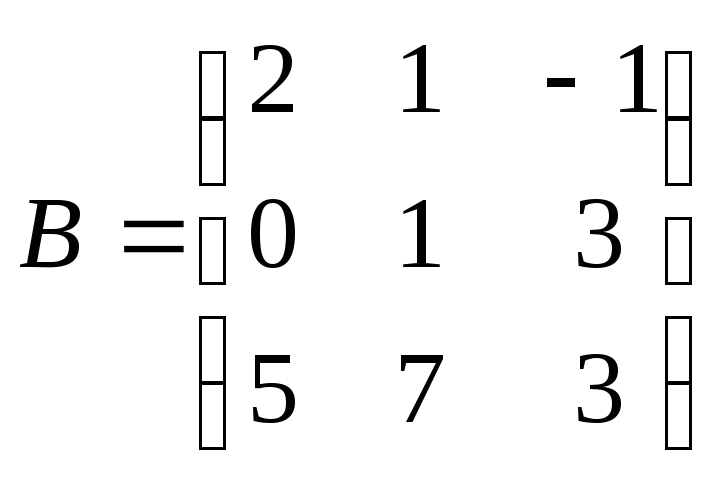9) Вычислить
определитель 
10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
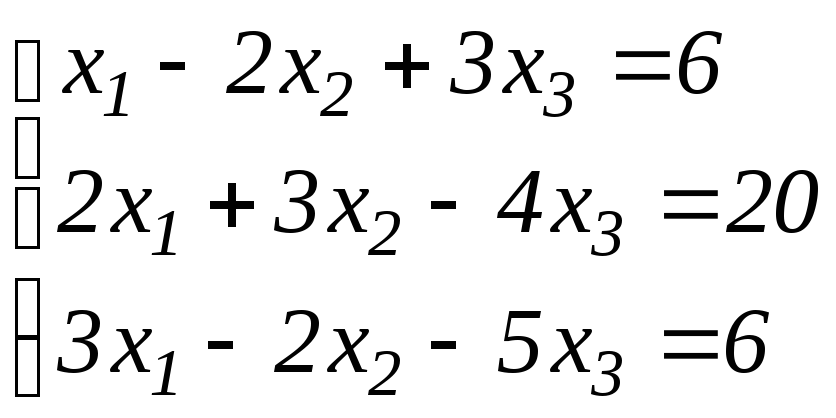
11) Найти все значения корня.
12) Найти пределы (не пользуясь правилом Лопиталя)
а)
б)
в)
г)
;
д)
13) Найти производные
данных функций:
14) Найти
и
а) у = ех
sin
x
б)
15) Найти производную указанного порядка.
16) Найти пределы пользуясь правилом Лопиталя
а)
б)
17) Найти первые и вторые частные производные
18) Провести полное исследование функции и построить их график.
Вариант 3
1)
Найти косинус угла между векторами
и
.
2) Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
3) Компланарны
ли векторы
,
и
?
4) Вычислить
площадь параллелограмма, построенного
на векторах
и
.
5) Найти расстояние
от точки
до плоскости, проходящей через точки
.
6) Написать
уравнение плоскости, проходящей через
точку
перпендикулярно вектору
.
7) Исследовать кривую второго порядка и построить ее.
8) Вычислить.
где
,
.
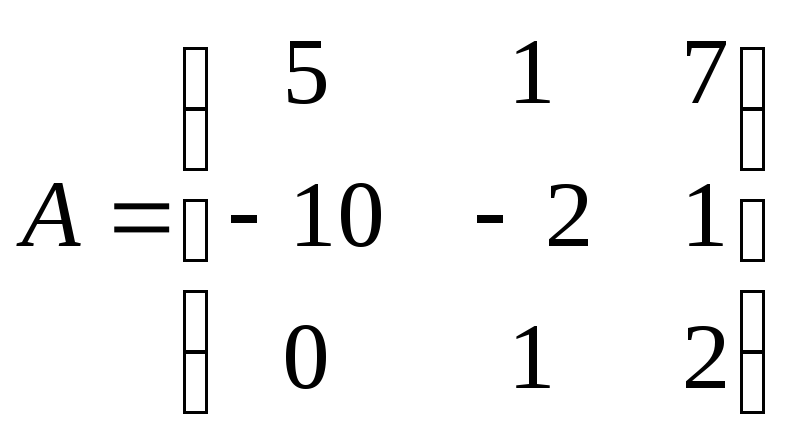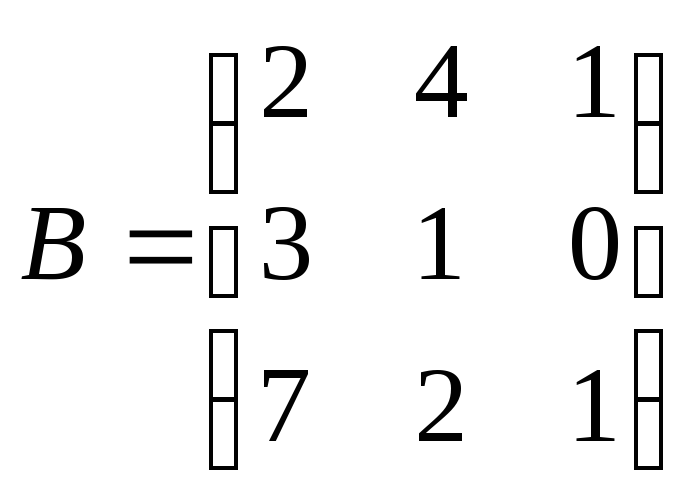9) Вычислить
определитель 
10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
11) Найти все значения корня.
12) Найти пределы (не пользуясь правилом Лопиталя)
а)
б)
в)
г)
д)
13) Найти производные
данных функций:
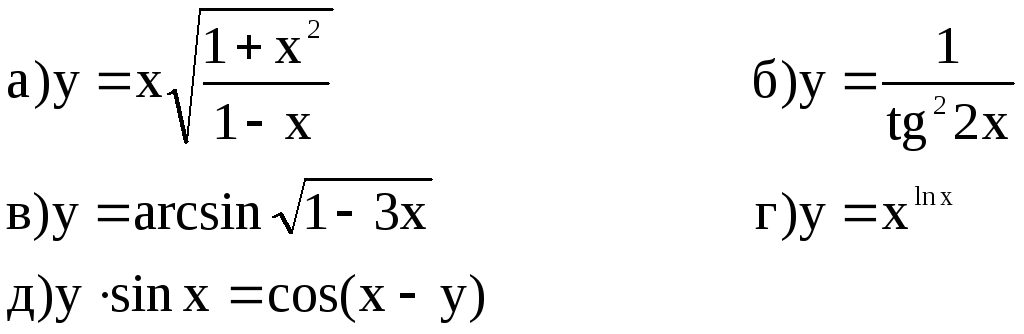
14) Найти
и
а) у =
б)
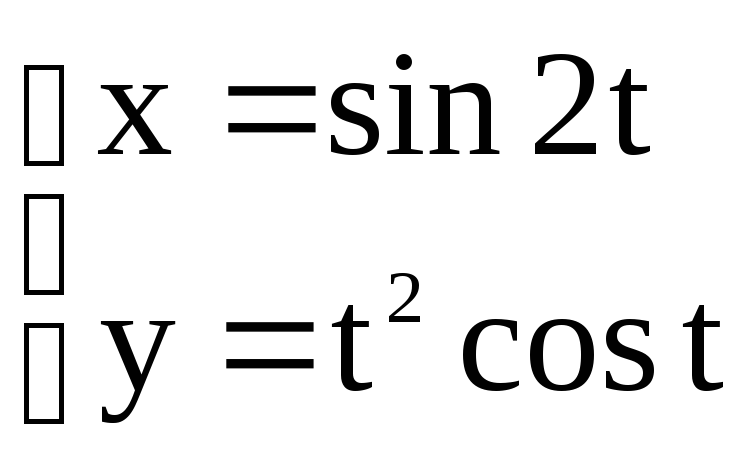
15) Найти производную указанного порядка.
16) Найти пределы пользуясь правилом Лопиталя
а)
б)
17) Найти первые и вторые частные производные
18) Провести полное исследование функции и построить их график.
Вариант 4
1)
Найти косинус угла между векторами
и
.
2) Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
3) Компланарны
ли векторы
,
и
?
4) Вычислить
площадь параллелограмма, построенного
на векторах
и
.
5) Найти расстояние
от точки
до плоскости, проходящей через точки
.
6) Написать
уравнение плоскости, проходящей через
точку
перпендикулярно вектору
.
7) Исследовать кривую второго порядка и построить ее.
8) Вычислить.
где
,
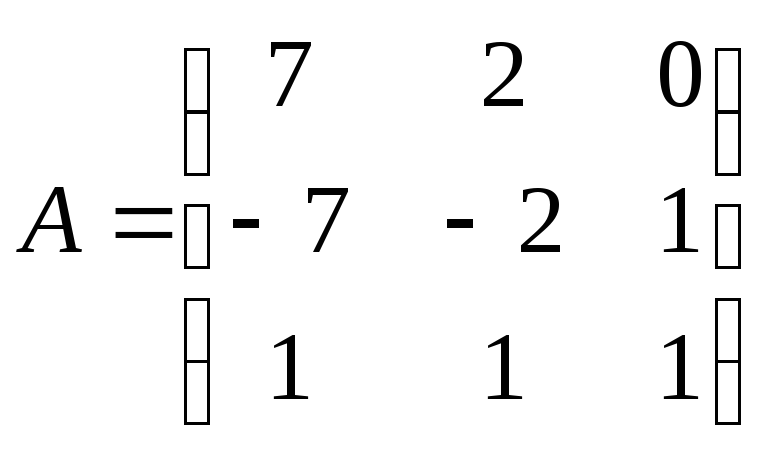9) Вычислить
определитель 
10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
11) Найти все значения корня.
12) Найти пределы (не пользуясь правилом Лопиталя)
а)
б)
в)
г)
д)
13) Найти производные
данных функций:
14) Найти
и
а) у = lntg3
x
б)
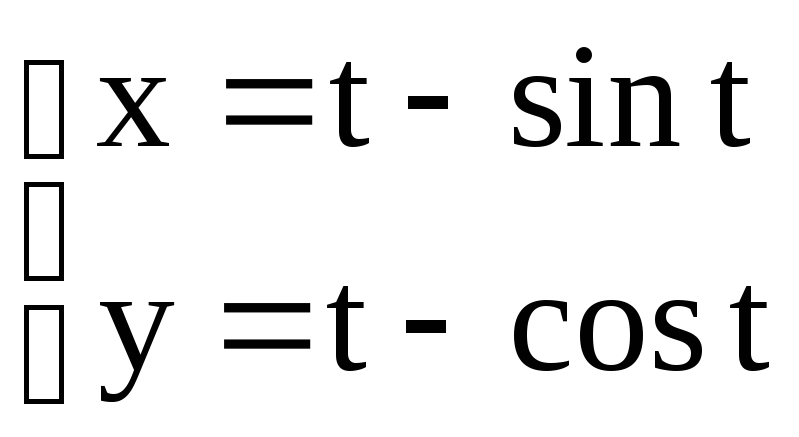
15) Найти производную указанного порядка.
16) Найти пределы пользуясь правилом Лопиталя
а)
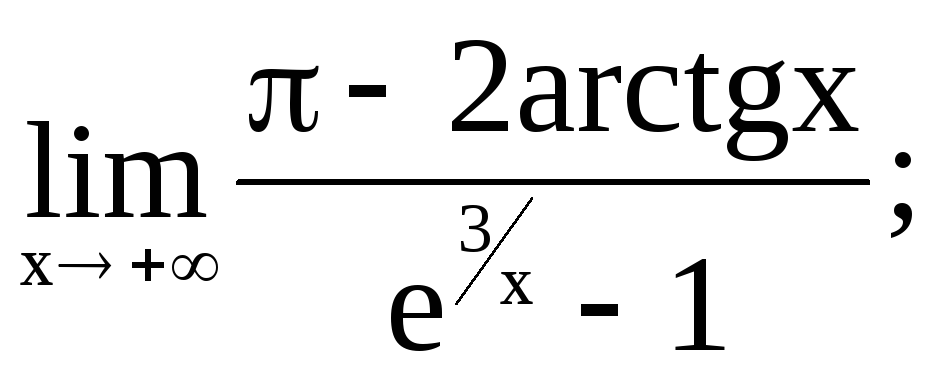б)
17) Найти первые и вторые частные производные
18) Провести полное исследование функции и построить их график.
Вариант 5
1)
Найти косинус угла между векторами
и
.
2) Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
3) Компланарны
ли векторы
,
и
?
4) Вычислить
площадь параллелограмма, построенного
на векторах
и
.
5) Найти расстояние
от точки
до плоскости, проходящей через точки
.
6) Написать
уравнение плоскости, проходящей через
точку
перпендикулярно вектору
.
7) Исследовать кривую второго порядка и построить ее.
8) Вычислить.
где
,
.
9) Вычислить
определитель 
10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
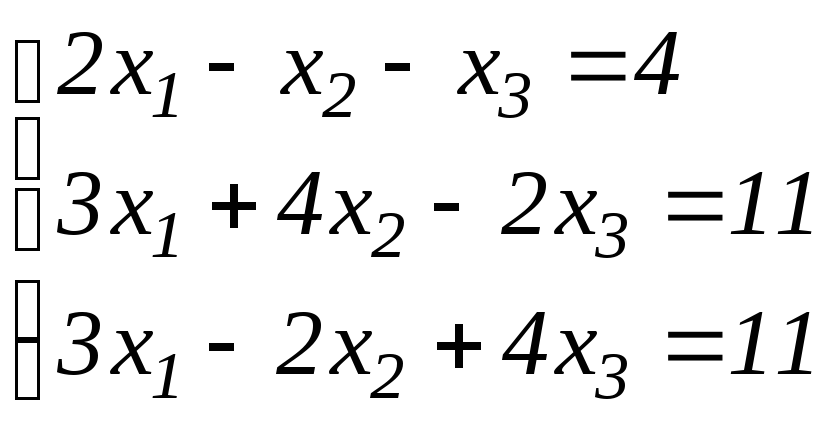
11) Найти все значения корня.
12) Найти пределы (не пользуясь правилом Лопиталя)
а)
б)
в)
г)
д)
13) Найти производные
данных функций:
14) Найти
и
а) у =
б)
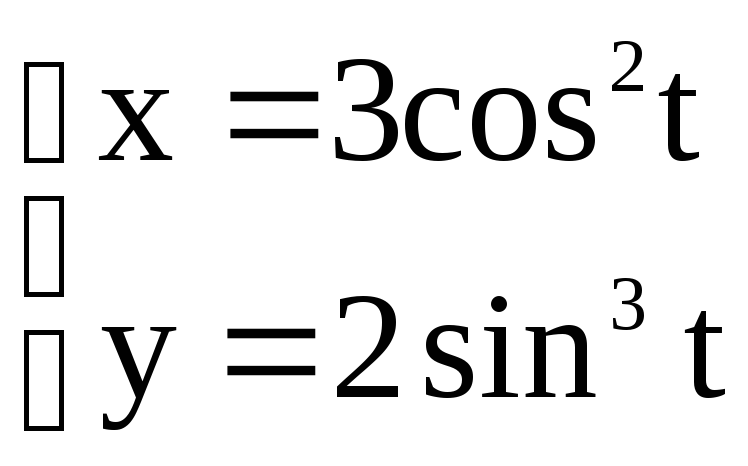
15) Найти производную указанного порядка.
16) Найти пределы пользуясь правилом Лопиталя
а)
б)
17) Найти первые и вторые частные производные
18) Провести полное исследование функции и построить их график.
Вариант 6
1)
Найти косинус угла между векторами
и
.
2) Коллинеарны
ли векторы
и
,
построенные по векторам
и
?
3) Компланарны
ли векторы
,
и
?
4) Вычислить
площадь параллелограмма, построенного
на векторах
и
.
5) Найти расстояние
от точки
до плоскости, проходящей через точки
.
6) Написать
уравнение плоскости, проходящей через
точку
перпендикулярно вектору
.
7) Исследовать кривую второго порядка и построить ее.
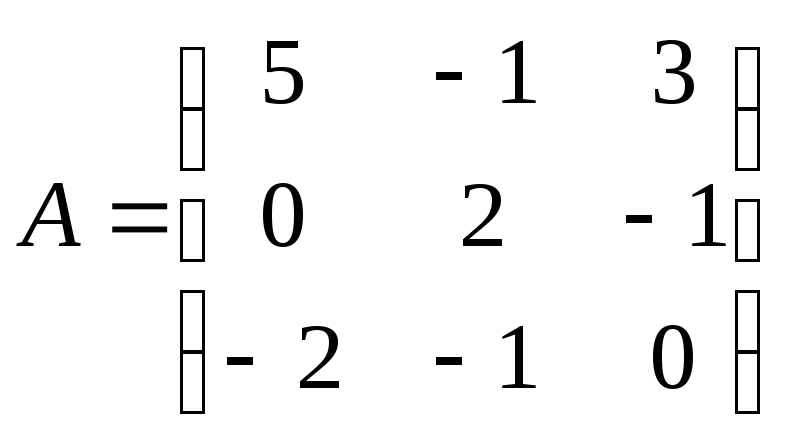
8) Вычислить.
где
,
.
9) Вычислить
определитель 
10) Решить систему линейных алгебраических уравнений тремя методами (матричным, Крамера, Гаусса)
11) Найти все значения корня.
12) Найти пределы (не пользуясь правилом Лопиталя)
а)
б)
в)
г)
д)
13) Найти производные
данных функций:
14) Найти
и
а) у = excos
x
б)
15) Найти производную указанного порядка.
16) Найти пределы пользуясь правилом Лопиталя
а)
б)
17) Найти первые и вторые частные производные
18) Провести полное исследование функции и построить их график.
Вариант 7
1)
Найти косинус угла между векторами
и
.
