
Расчетная работа по дисциплине «Методы оптимальных решений»
Вариант 7
Задание 1
Игры с природой
Предприятие общественного питания
планирует выпуск трех партий новых,
ранее не производимых полуфабрикатов
П1, П2, П3, в условиях
неясной рыночной конъюнктуры, относительно
которой известны лишь отдельные возможные
состояния![]() ,
,![]() ,
,![]() ,
,![]() ,
а также возможные объемы товарооборота
по каждому варианту и их условные
вероятности, которые представлены в
виде (
,
а также возможные объемы товарооборота
по каждому варианту и их условные
вероятности, которые представлены в
виде (![]() )
матрицы. Определить предпочтительный
план выпуска полуфабрикатов.
)
матрицы. Определить предпочтительный
план выпуска полуфабрикатов.
![]() =
0,6
=
0,6
|
Партии полуфабрикатов |
Объем товарооборота при различных состояний рыночной конъюнктуры | ||
|
|
|
| |
|
П1 |
9 0,6 |
6 0,3 |
4 0,1 |
|
П2 |
8 0,2 |
3 0,7 |
7 0,1 |
|
П3 |
5 0,1 |
5 0,4 |
8 0,5 |
Решение:
Максимальный критерий Вальда.
Воспользуемся формулой:
W=![]()
Где ![]() - это элемент матрицы выигрышей.
- это элемент матрицы выигрышей.
Сначала из каждой строки матрицы выбираем минимальный элемент, а затем среди полученных значений выбираем максимальное. Таким образом, получаем:
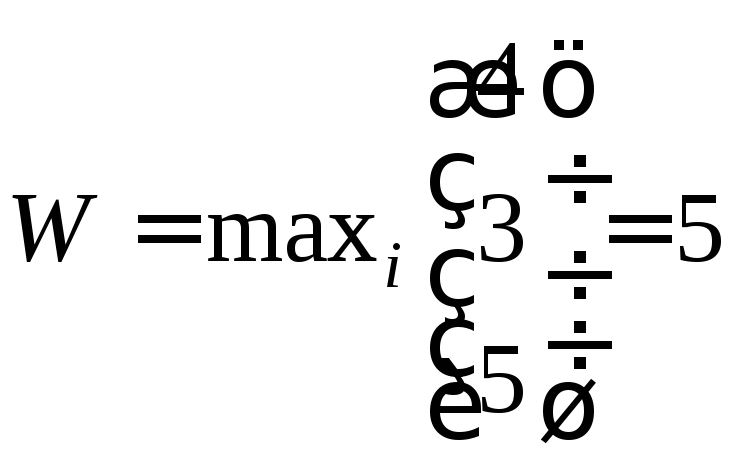
что соответствует стратегии П3. Таким образом, согласно критерию Вальда, наилучшей является стратегия П3, гарантирующая выигрыш, равный 5.
Критерий минимального риска Сэвиджа.
S=![]() ̓
̓
Где ![]() - это элемент матрицы рисков, которая
получается из матрицы выигрышей по
формуле:
- это элемент матрицы рисков, которая
получается из матрицы выигрышей по
формуле:
![]() =
=![]() -
-![]()
Матрица рисков имеет ту же размерность, что и матрица выигрышей, и формируется по столбцам матрицы выигрышей. В каждом столбце максимальный элемент заменятся нулем, а остальные элементы получаются как результат вычитания соответствующего элемента матрицы выигрыша из максимального в своем столбце. Таким образом в данном случае получаем:
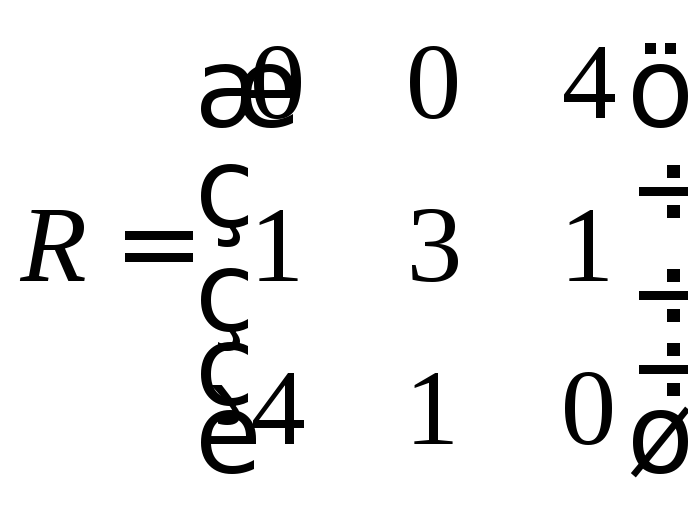
Теперь применяем формулу:
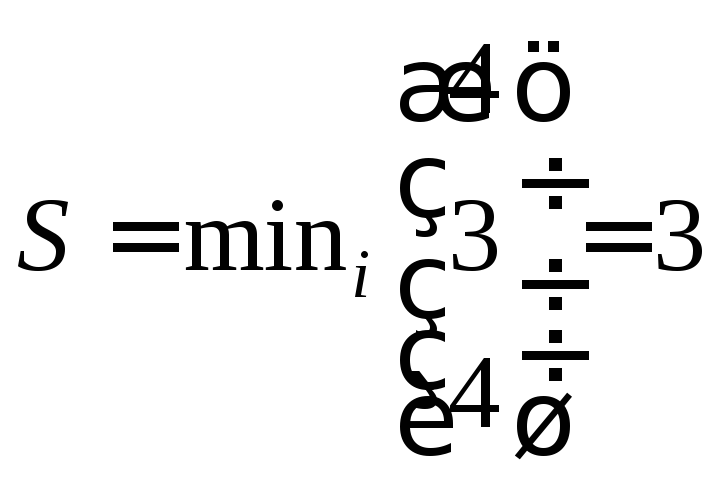
Минимум дает стратегия П2, которая является наилучшей с точки зрения критерия Сэвиджа.
Критерий пессимизма – оптимизма Гурвица.Согласно этому критерию, оптимальной считается стратегия, для которой выполняется соотношения:
G
= ![]() [
[ ![]()
![]() + (1 -
+ (1 - ![]() )
)
![]() ],
],
При . Получим:

Согласно критерию Гурвица, оптимальной следует считать стратегию П3. Как видим, эта стратегия появляется в качестве оптимальной второй раз.
Критерий максимума математического ожидания выигрыша.
М i
=![]() ij P
ij
ij P
ij
Таким образом, для рассматриваемых условий имеем:
М1= 9* 0,6 + 6 * 0,3 + 4 * 0,1 = 7,6
М2= 8 * 0,2 + 3 * 0,7 + 7 * 0,1 = 4,4
М3= 5 * 0,1 + 5 * 0,4 + 8 * 0,5 = 6,5
По
критерию максимума математического
ожидания выигрыша имеем ![]()
![]() = 7,6, что соответствует наилучшей стратегии
П1.
= 7,6, что соответствует наилучшей стратегии
П1.
Критерий минимального среднего риска.
Ri =![]() ij
P ij
ij
P ij
R1= 0* 0,6 + 0 * 0,3 + 4 * 0,1 = 0,4
R2= 1 * 0,2 + 3 * 0,7 + 1 * 0,1 = 2,4
R3= 4 * 0,1 + 1 * 0,4 + 0* 0,5 = 0,8
Отсюда
![]() = 0,4, что соответствует наилучшей стратегии
П1.
= 0,4, что соответствует наилучшей стратегии
П1.
Вывод:
Согласно критерию Сэвиджа, наилучшей является стратегия П2. По критериям Вальда и Гурвица, оптимальной следует считать стратегию П3. Критерии Байеса и минимального среднего риска показывает, что наилучшая стратегия П1.
По совокупности критериев в данном случае оптимальными следует принять стратегии П1и П3.
