
- •Физические основы механики.
- •Кинематика материальной точки.
- •Скорость материальной точки.
- •Ускорение материальной точки.
- •Тангенциальное и нормальное ускорение.
- •Проекции скорости и ускорения
- •График скорости
- •Вращательное движение твердого тела.
- •Равномерное движение по окружности
- •Период и частота
- •Кинематика вращательного движения
- •Угловое ускорение вращающегося тела
- •Связь углового и линейного ускорений
- •Основные уравнения кинематики
- •Динамика частиц
- •Основные законы классической динамики. I закон Ньютона
- •Механические системы
- •Масса. Импульс
- •Закон сохранения импульса. II закон Ньютона
- •II закон Ньютона:
- •Силы в механике
- •1. Силы тяготения (гравитационные силы).
- •2. Силы упругости.
- •3. Сила трения скольжения.
- •Принцип независимости действия сил
- •III закон Ньютона
- •III закон Ньютона:
- •Системы материальных точек. Центр инерции
- •Закон сохранения центра инерции
- •Теорема о движении центра масс
- •Механическая работа. Мощность
- •Кинетическая энергия
- •Консервативные и неконсервативные силы. Потенциальная энергия.
- •Свойства потенциальных полей.
- •Закон сохранения энергии в механике. Общефизический закон сохранения.
- •Абсолютно упругий и абсолютно неупругий центральные удары.
- •Твердое тело в механике. Уравнение вращательного движения твердого тела относительно точки.
- •Уравнение вращательного движения твердого тела относительно неподвижной оси.
- •Момент импульса тела относительно неподвижной оси.
- •Момент инерции твердых тел. Теорема Штейнера.
- •Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему
- •Кинетическая энергия тела, вращающегося вокруг неподвижной оси.
- •Работа при вращательном движении.
- •Закон сохранения момента импульса.
- •Элементы специальной теории относительности. Принцип относительности в механике.
- •Постулаты специальной теории относительности.
- •Относительность одновременности.
- •Преобразования Лоренца.
- •Следствия из преобразований Лоренца.
- •Длительность событий в различных инерциальных системах отсчета.
- •Релятивистский закон сложения скоростей.
- •Интервал.
- •Собственное время.
- •Элементы релятивистской динамики. Релятивистский импульс
- •Уравнение движения релятивистской частицы.
- •Закон взаимосвязи массы и энергии.
- •Связь энергии и импульса.
- •Инварианты преобразования.
2. Силы упругости.
Силы упругости возникают в результате взаимодействия тел, сопровождающегося их деформацией.
Упругая сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия:
![]()
где
![]() - радиус-вектор, характеризующий смещение
частицы из положения равновесия,k
– коэффициент упругости.
- радиус-вектор, характеризующий смещение
частицы из положения равновесия,k
– коэффициент упругости.
Примером силы упругости является сила упругости деформации пружины при растяжении или сжатии:
![]()
где k – жесткость пружины, x – упругая деформация.
3. Сила трения скольжения.
Сила трения скольжения возникает при скольжении одного тела по поверхности другого:
![]()
где k – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей, N – сила нормального давления, прижимающая трущиеся поверхности друг к другу.
Сила трения скольжения направлена по касательной к трущимся поверхностям в сторону, противоположную движению рассматриваемого тела относительно другого.
Принцип независимости действия сил
В механике большое значение имеет принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно II закону Ньютона, как будто других сил не было. Согласно этому принципу силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач.
Например, нормальное и тангенциальное ускорения материальной точки определяются соответствующими составляющими силы:
![]()
![]()
![]()
![]()
![]()
![]()
Сила
![]() ,
сообщающая материальной точке нормальное
ускорение, направлена к центру кривизны
траектории и поэтому называетсяцентростремительной
силой.
,
сообщающая материальной точке нормальное
ускорение, направлена к центру кривизны
траектории и поэтому называетсяцентростремительной
силой.
III закон Ньютона
Рассмотрим
замкнутую систему, состоящую из двух
частиц, взаимодействующих с силами
![]() и
и![]() ,
,![]() и
и![]() - импульсы этих частиц.
- импульсы этих частиц.
Для замкнутой системы справедлив закон сохранения импульса:
![]()
Дифференцируя это соотношение по времени
![]()
На основании (3)
получим
![]() или
или![]() (21)
(21)
III закон Ньютона:
Всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
Как и II закон Ньютона, он выполняется только в инерциальных системах отсчета.
Системы материальных точек. Центр инерции
|
|
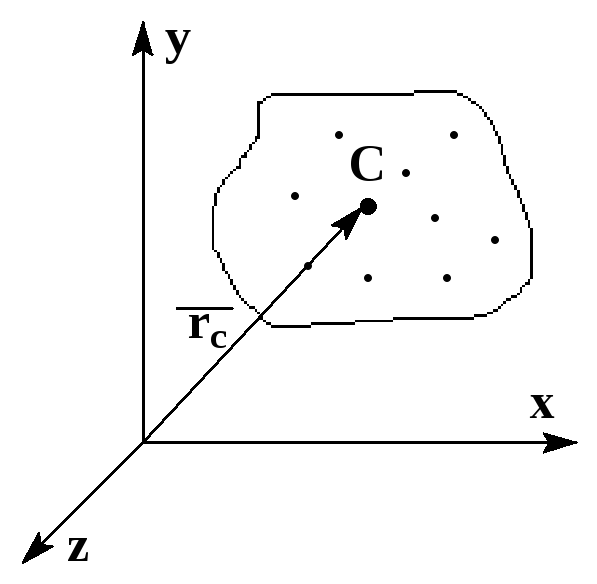
Рассмотрим систему n материальных точек. Центром инерции или центром масс системы материальных точек называют такую точку C, радиус-вектор которой равен:
|
где
![]() и
и![]() - масса и радиус-векторi-той
точки
- масса и радиус-векторi-той
точки
M – масса системы n точек.
Закон сохранения центра инерции
Продифференцируем по времени (22):
![]() (23)
(23)
Для изолированной
системы
![]() ,
отсюда
,
отсюда![]() ,
т.е. центр масс изолированной системы
движется с постоянной по величине и
направлению скоростью, хотя скорости
отдельных точек могут меняться с течением
времени –закон
сохранения центра инерции.
,
т.е. центр масс изолированной системы
движется с постоянной по величине и
направлению скоростью, хотя скорости
отдельных точек могут меняться с течением
времени –закон
сохранения центра инерции.
При изучении движения систем материальных точек систему отсчета связывают с центром инерции тела. Эту систему отсчета называют системой центра инерции.
![]() ,
,
т.е. импульс системы материальных точек связан со скоростью центра инерции так же, как импульс и скорость одной частицы.

 (22)
(22)