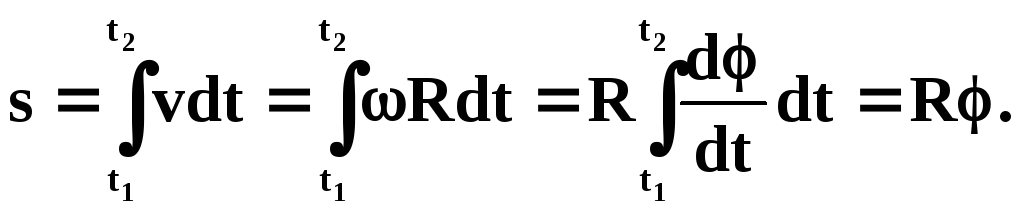- •Физические основы механики.
- •Кинематика материальной точки.
- •Скорость материальной точки.
- •Ускорение материальной точки.
- •Тангенциальное и нормальное ускорение.
- •Проекции скорости и ускорения
- •График скорости
- •Вращательное движение твердого тела.
- •Равномерное движение по окружности
- •Период и частота
- •Кинематика вращательного движения
- •Угловое ускорение вращающегося тела
- •Связь углового и линейного ускорений
- •Основные уравнения кинематики
- •Динамика частиц
- •Основные законы классической динамики. I закон Ньютона
- •Механические системы
- •Масса. Импульс
- •Закон сохранения импульса. II закон Ньютона
- •II закон Ньютона:
- •Силы в механике
- •1. Силы тяготения (гравитационные силы).
- •2. Силы упругости.
- •3. Сила трения скольжения.
- •Принцип независимости действия сил
- •III закон Ньютона
- •III закон Ньютона:
- •Системы материальных точек. Центр инерции
- •Закон сохранения центра инерции
- •Теорема о движении центра масс
- •Механическая работа. Мощность
- •Кинетическая энергия
- •Консервативные и неконсервативные силы. Потенциальная энергия.
- •Свойства потенциальных полей.
- •Закон сохранения энергии в механике. Общефизический закон сохранения.
- •Абсолютно упругий и абсолютно неупругий центральные удары.
- •Твердое тело в механике. Уравнение вращательного движения твердого тела относительно точки.
- •Уравнение вращательного движения твердого тела относительно неподвижной оси.
- •Момент импульса тела относительно неподвижной оси.
- •Момент инерции твердых тел. Теорема Штейнера.
- •Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему
- •Кинетическая энергия тела, вращающегося вокруг неподвижной оси.
- •Работа при вращательном движении.
- •Закон сохранения момента импульса.
- •Элементы специальной теории относительности. Принцип относительности в механике.
- •Постулаты специальной теории относительности.
- •Относительность одновременности.
- •Преобразования Лоренца.
- •Следствия из преобразований Лоренца.
- •Длительность событий в различных инерциальных системах отсчета.
- •Релятивистский закон сложения скоростей.
- •Интервал.
- •Собственное время.
- •Элементы релятивистской динамики. Релятивистский импульс
- •Уравнение движения релятивистской частицы.
- •Закон взаимосвязи массы и энергии.
- •Связь энергии и импульса.
- •Инварианты преобразования.
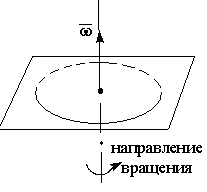
Кинематика вращательного движения
|
|
При
вращении твердого тела вокруг
неподвижной оси OO’
точка M
этого тела с радиус-вектором
|
Для указания
направления вращения малым углам
поворота приписывают направление:
![]() направлен по оси вращения так, чтобы
рассматриваемое с его конца вращение
происходило против часовой стрелки
(правило правого винта). Если тело сделалоN
поворотов:
направлен по оси вращения так, чтобы
рассматриваемое с его конца вращение
происходило против часовой стрелки
(правило правого винта). Если тело сделалоN
поворотов:![]() .
Средняя угловая скорость:
.
Средняя угловая скорость:
![]() (11)
(11)
Мгновенная угловая скорость:
![]() (12)
(12)
|
|
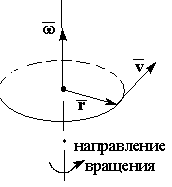
Направление
Если тело делает
оборотов в сек, то его угловая скорость
Связь линейной и угловой скоростей:
|
или
![]() (13)
(13)
в векторной форме:
![]() (14)
(14)
Угловое ускорение вращающегося тела
Отношение
![]() называетсясредним
угловым ускорением.
называетсясредним
угловым ускорением.
|
|
Угловое ускорение в заданный момент времени:
Вектор
углового ускорения
|
Связь углового и линейного ускорений
Продифференцируем (14) по времени:
![]() (16)
(16)
Первое слагаемое
– тангенциальное ускорение
![]() ,
т.к. вектор
,
т.к. вектор![]() по правилу векторного произведения
направлен по касательной к траектории
и по модулю равен:
по правилу векторного произведения
направлен по касательной к траектории
и по модулю равен:
![]()
|
|
Второе слагаемое
– нормальное ускорение, т.к. вектор
|
Основные уравнения кинематики
|
Поступательное движение |
Вращательное движение |
|
Равномерное | |
|
|
|
|
|
|
|
|
|
|
|
|
|
Равнопеременное | |
|
|
|
|
|
|
|
|
|
|
|
|
|
Неравномерное | |
|
|
|
|
|
|
|
|
|
|
Связь линейных и угловых параметров | |
|
|
|
|
|
|
|
| |
Динамика частиц
Динамика рассматривает механическое движение с учетом причин, вызывающих это движение или изменение этого движения.
Основная задача динамики: для физической системы, находящейся в определенных внешних условиях, найти уравнение движения.
Уравнениями движения называются уравнения, описывающие изменение состояния системы во времени.
В классической
механике состояние частиц полностью
определяется заданием ее координат x,
y,
z
и составляющих скорости vx,
vy,
vz,
т.е. заданием радиус-вектора
![]() и скорости
и скорости![]() .
.
Состояние системы
из N
нерелятивистских частиц определяется
заданием радиус-векторов
![]() ,
,![]() ,
…,
,
…,![]() и скоростей
и скоростей![]() ,
,![]() ,
…,
,
…,![]() всех частиц в данный момент времени.
всех частиц в данный момент времени.
В самом общем виде уравнения движения системы частиц может быть записано в виде
![]()
Вид функции
![]() зависит от свойств частиц системы и
внешних условий, в которых они движутся
зависит от свойств частиц системы и
внешних условий, в которых они движутся
Общее решение уравнения может быть найдено, если известны:
вид функции
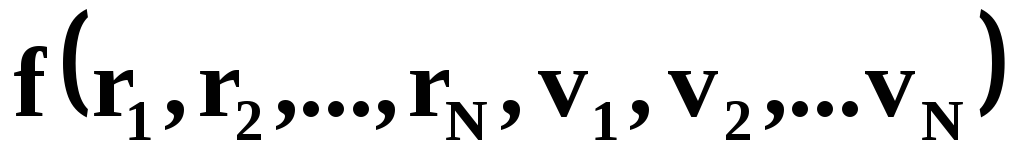 и
иначальные условия, т.е. значения
 и
и в момент времениt=0/
в момент времениt=0/