
- •Физические основы механики.
- •Кинематика материальной точки.
- •Скорость материальной точки.
- •Ускорение материальной точки.
- •Тангенциальное и нормальное ускорение.
- •Проекции скорости и ускорения
- •График скорости
- •Вращательное движение твердого тела.
- •Равномерное движение по окружности
- •Период и частота
- •Кинематика вращательного движения
- •Угловое ускорение вращающегося тела
- •Связь углового и линейного ускорений
- •Основные уравнения кинематики
- •Динамика частиц
- •Основные законы классической динамики. I закон Ньютона
- •Механические системы
- •Масса. Импульс
- •Закон сохранения импульса. II закон Ньютона
- •II закон Ньютона:
- •Силы в механике
- •1. Силы тяготения (гравитационные силы).
- •2. Силы упругости.
- •3. Сила трения скольжения.
- •Принцип независимости действия сил
- •III закон Ньютона
- •III закон Ньютона:
- •Системы материальных точек. Центр инерции
- •Закон сохранения центра инерции
- •Теорема о движении центра масс
- •Механическая работа. Мощность
- •Кинетическая энергия
- •Консервативные и неконсервативные силы. Потенциальная энергия.
- •Свойства потенциальных полей.
- •Закон сохранения энергии в механике. Общефизический закон сохранения.
- •Абсолютно упругий и абсолютно неупругий центральные удары.
- •Твердое тело в механике. Уравнение вращательного движения твердого тела относительно точки.
- •Уравнение вращательного движения твердого тела относительно неподвижной оси.
- •Момент импульса тела относительно неподвижной оси.
- •Момент инерции твердых тел. Теорема Штейнера.
- •Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему
- •Кинетическая энергия тела, вращающегося вокруг неподвижной оси.
- •Работа при вращательном движении.
- •Закон сохранения момента импульса.
- •Элементы специальной теории относительности. Принцип относительности в механике.
- •Постулаты специальной теории относительности.
- •Относительность одновременности.
- •Преобразования Лоренца.
- •Следствия из преобразований Лоренца.
- •Длительность событий в различных инерциальных системах отсчета.
- •Релятивистский закон сложения скоростей.
- •Интервал.
- •Собственное время.
- •Элементы релятивистской динамики. Релятивистский импульс
- •Уравнение движения релятивистской частицы.
- •Закон взаимосвязи массы и энергии.
- •Связь энергии и импульса.
- •Инварианты преобразования.
Уравнение движения релятивистской частицы.
Записывая II закон Ньютона в виде:
![]()
и подставляя в него релятивистский импульс, получим уравнение движения релятивистской частицы:
 (85)
(85)
II
закон Ньютона оказывается инвариантным
относительно преобразований Лоренца,
если под импульсом понимать вектор
![]() ,
равный:
,
равный:
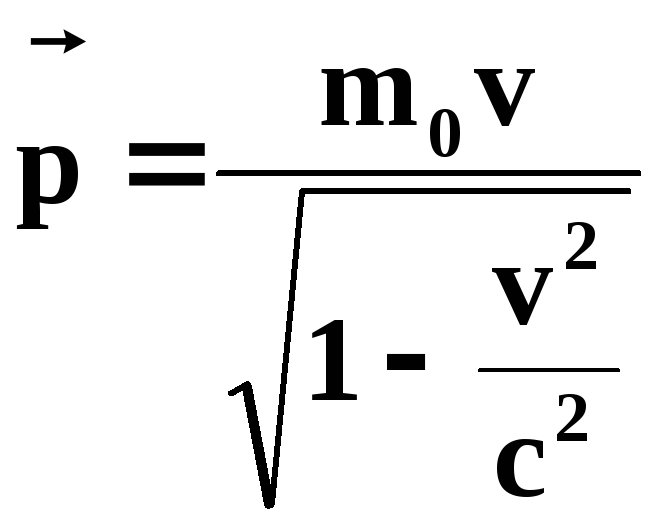
Закон взаимосвязи массы и энергии.
Как известно
элементарная работа силы
![]() равна приращению кинетической энергии
частицы:
равна приращению кинетической энергии
частицы:
![]() (86)
(86)
Подставим в (86)
![]() из (85):
из (85):

учтем, что
![]() ,
и
,
и![]()

Найдем дифференциал выражения (84):
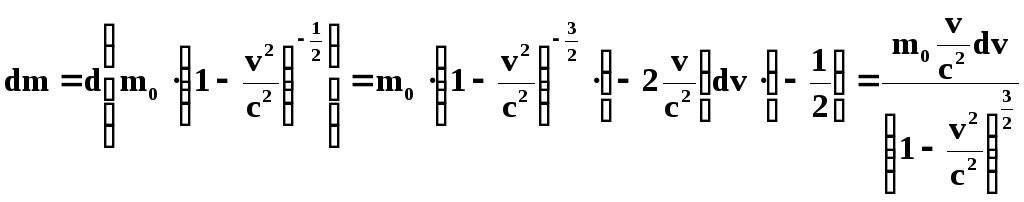 (88)
(88)
И сравним (87) и (88). Из сравнения видно, что:
![]() (89)
(89)
Интегрирование
этого соотношения в пределах от
![]() (если
(если![]() ,
,![]() и кинетическая энергия равна нулю) до
и кинетическая энергия равна нулю) до![]() дает:
дает:
 (90)
(90)
Преобразуя (19) с учетом (84):
 (91)
(91)
мы получили выражение для кинетической энергии в СТО.
Из формулы
![]() следует, чтоприращение
кинетической энергии частицы сопровождается
пропорциональным приращением ее
релятивистской массы.
Однако при протекании различных процессов
в природе одни виды энергии переходят
в другие, поэтому естественно ожидать,
что маска тела будет возрастать при
любом увеличении общего запаса энергии
тела независимо от того, за счет какого
конкретного вида энергии это увеличение
происходит, т.е.:
следует, чтоприращение
кинетической энергии частицы сопровождается
пропорциональным приращением ее
релятивистской массы.
Однако при протекании различных процессов
в природе одни виды энергии переходят
в другие, поэтому естественно ожидать,
что маска тела будет возрастать при
любом увеличении общего запаса энергии
тела независимо от того, за счет какого
конкретного вида энергии это увеличение
происходит, т.е.:
![]()
![]() (94)
(94)
где
![]() - полная энергия тела.
- полная энергия тела.
Т.о., Эйнштейн пришел к фундаментальному выводу:
полная энергия тела и его релятивистская масса всегда пропорциональны друг другу.
Этот закон носит название закона взаимосвязи релятивистской массы и энергии. Он объединяет закон сохранения массы и закон сохранения энергии в единый закон сохранения массы и энергии.
Связь энергии и импульса.
Соотношение
![]() возведем
в квадрат.
возведем
в квадрат.
 (95)
(95)
В числителе прибавим
и отнимем
![]() :
:

Или
![]()
Отсюда получим:
![]() (96)
(96)
или:
![]() (97)
(97)
Т.к.
![]() ,
то
,
то
![]() (98)
(98)
Из формул
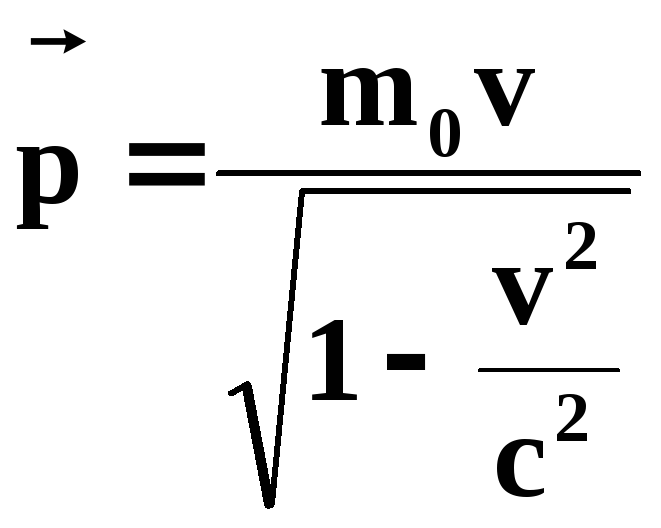 и
и

легко получить еще одно соотношение, связывающее энергию и импульс частицы в релятивистской механике:
![]() (99)
(99)
Инварианты преобразования.
При изучении СТО мы установили существование целого ряда инвариантных величин, т.е. величин, не меняющихся при переходе от одной инерциальной системы отсчета к другой.
Перечислим их:
скорость света в вакууме (с);
интервал между событиями:
 ;
;собственное время
 системы;
системы;масса покоя
 .
.
Покажем, что
существует еще один инвариант
![]() .
Из уравнения (95) следует, что:
.
Из уравнения (95) следует, что:
![]()
Откуда:
![]() (100)
(100)
т.к. масса покоя и скорость света инвариантны относительно преобразований Лоренца.
Из (100) следует, что в СТО все законы сохранения энергии и импульса перестают быть независимыми, а объединяются в единый закон сохранения импульса-энергии.
