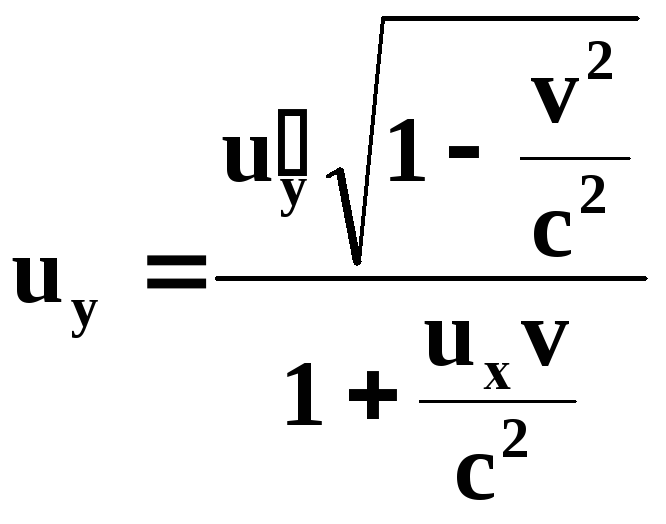- •Физические основы механики.
- •Кинематика материальной точки.
- •Скорость материальной точки.
- •Ускорение материальной точки.
- •Тангенциальное и нормальное ускорение.
- •Проекции скорости и ускорения
- •График скорости
- •Вращательное движение твердого тела.
- •Равномерное движение по окружности
- •Период и частота
- •Кинематика вращательного движения
- •Угловое ускорение вращающегося тела
- •Связь углового и линейного ускорений
- •Основные уравнения кинематики
- •Динамика частиц
- •Основные законы классической динамики. I закон Ньютона
- •Механические системы
- •Масса. Импульс
- •Закон сохранения импульса. II закон Ньютона
- •II закон Ньютона:
- •Силы в механике
- •1. Силы тяготения (гравитационные силы).
- •2. Силы упругости.
- •3. Сила трения скольжения.
- •Принцип независимости действия сил
- •III закон Ньютона
- •III закон Ньютона:
- •Системы материальных точек. Центр инерции
- •Закон сохранения центра инерции
- •Теорема о движении центра масс
- •Механическая работа. Мощность
- •Кинетическая энергия
- •Консервативные и неконсервативные силы. Потенциальная энергия.
- •Свойства потенциальных полей.
- •Закон сохранения энергии в механике. Общефизический закон сохранения.
- •Абсолютно упругий и абсолютно неупругий центральные удары.
- •Твердое тело в механике. Уравнение вращательного движения твердого тела относительно точки.
- •Уравнение вращательного движения твердого тела относительно неподвижной оси.
- •Момент импульса тела относительно неподвижной оси.
- •Момент инерции твердых тел. Теорема Штейнера.
- •Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему
- •Кинетическая энергия тела, вращающегося вокруг неподвижной оси.
- •Работа при вращательном движении.
- •Закон сохранения момента импульса.
- •Элементы специальной теории относительности. Принцип относительности в механике.
- •Постулаты специальной теории относительности.
- •Относительность одновременности.
- •Преобразования Лоренца.
- •Следствия из преобразований Лоренца.
- •Длительность событий в различных инерциальных системах отсчета.
- •Релятивистский закон сложения скоростей.
- •Интервал.
- •Собственное время.
- •Элементы релятивистской динамики. Релятивистский импульс
- •Уравнение движения релятивистской частицы.
- •Закон взаимосвязи массы и энергии.
- •Связь энергии и импульса.
- •Инварианты преобразования.
Следствия из преобразований Лоренца.
Длина тела в различных инерциальных системах отсчета.
|
|
Рассмотрим две системы отсчета: Oxyz – неподвижная инерциальная система и O’x’y’z’
– система отсчета, движущаяся
относительно первой со скоростью
|
Для определения
его длины надо отметить координаты
концов стержня:
![]() - длина покоящегося стержня.
- длина покоящегося стержня.
В системе Oxyz
стержень движется со скоростью
![]() .
Для определения его длины надо отметить
координаты концов стержня в один и тот
же момент времени
.
Для определения его длины надо отметить
координаты концов стержня в один и тот
же момент времени![]() по часам системыOxyz:
по часам системыOxyz:
![]() - длина движущегося стержня.
- длина движущегося стержня.
Выразим координаты
![]() и
и![]() концов стержня с помощью преобразований
Лоренца:
концов стержня с помощью преобразований
Лоренца:

![]() (67)
(67)
Из (67) видно, что
![]() ,
т.е. длина тела наибольшая в той системе,
по отношению к которой тело покоится.
Размеры тела в направлении осейy
и z
не меняются.
,
т.е. длина тела наибольшая в той системе,
по отношению к которой тело покоится.
Размеры тела в направлении осейy
и z
не меняются.
Сокращение длины движущегося тела в направлении движения называется релятивистским сокращением. Оно становится заметным при скоростях, близких к скорости света. Такие скорости называются релятивистскими.
Длительность событий в различных инерциальных системах отсчета.
|
|
Пусть в т. A, неподвижной в системе отсчета O’x’y’z’, произошло какое-то событие. Сравним длительность события в системах отсчета Oxyz и O’x’y’z’. В системе O’x’y’z’ т. A покоится, начало и конец события происходят в одной точке пространства и могут быть отмечены по одним и тем же часам: |
![]() - длительность
события в системе O’x’y’z’.
- длительность
события в системе O’x’y’z’.
По отношению к
системе Oxyz
т. A
движется, начало события происходит в
т.
![]() ,
а конец в т.
,
а конец в т.![]() ,
причем:
,
причем:
![]() (68)
(68)
где
![]() - длительность события в системеOxyz.
- длительность события в системеOxyz.
Моменты начала
![]() и конца
и конца![]() события должны быть отмечены по
синхронизированным часам системыOxyz,
находящимся в точках
события должны быть отмечены по
синхронизированным часам системыOxyz,
находящимся в точках
![]() и
и![]() .
Воспользуемся преобразованиями Лоренца:
.
Воспользуемся преобразованиями Лоренца:

откуда получим:
 (69)
(69)
Из (69) следует, что t0t, т.е. длительность события наименьшая в той системе, по отношению к которой т. A покоится. Это значит, что процессы в движущейся системе протекают медленнее, чем в неподвижной, движущиеся часы идут медленнее неподвижных.
Релятивистский закон сложения скоростей.
Обозначим:
![]() - скорость некоторой
т. A
в системе отсчета Oxyz;
- скорость некоторой
т. A
в системе отсчета Oxyz;
![]() - скорость той же
точки в системе отсчета O’x’y’z’,
движущейся вдоль оси x
со скоростью
- скорость той же
точки в системе отсчета O’x’y’z’,
движущейся вдоль оси x
со скоростью
![]() .
.
Как известно,
![]() ;
;
![]() ;
;![]() (70)
(70)
и
![]() ;
;![]() ;
;![]() (71)
(71)
Из преобразований Лоренца найдем:
 ;
;
![]() ;
;![]() ;
; ;
(72)
;
(72)
Разделив первые три равенства (72) на четвертое и используем (70) и (71):


|
|
(73) |
|
(74) |
|
|
| ||
|
|
|
Легко видеть,
что при
![]() и
и![]() релятивистский закон сложения скоростей
переходит в классический.
релятивистский закон сложения скоростей
переходит в классический.