- •Электростатика
- •1.1. Электрические заряды
- •1.2. Закон Кулона. Электрическое поле
- •1.3. Дальнодействие и близкодействие
- •Частица – поле – частица,
- •1.4. Напряженность электрического поля
- •1.5. Принцип суперпозиции
- •1.6. Потенциальный характер электростатического поля
- •1.7. Потенциал. Разность потенциалов
- •1.8. Графическое изображение электростатических полей
- •1.9. Связь напряженности и потенциала
- •1.10. Поток вектора напряженности электрического поля
- •1.11. Теорема Гаусса
- •1.12. Применение теоремы Гаусса
- •3. Поле бесконечной нити, заряженной с линейной плотностью
- •2. Проводники в электрическом поле.
- •2.1. Электрическая емкость.
- •2.3. Энергия электрического поля.
- •2.3.1. Энергия системы электрических зарядов.
- •2.3.2. Энергия заряженного проводника.
- •2.3.3. Энергия заряженного конденсатора.
- •2.3.4. Энергия электрического поля.
- •2.4. Диэлектрики в электрическом поле.
- •2.4.1. Поляризация диэлектриков.
- •2.4.2. Основные соотношения электростатики для поля внутри диэлектрика.
- •2.4.2.1. Вектор электрического смещения. Граница двух диэлектриков
- •3.2. Постоянный электрический ток
- •3.2.1. Сила и плотность тока
- •3.2.2. Закон Ома в интегральной и дифференциальной форме
- •3.2.3. Сторонние силы. Закон Ома для цепи, содержащей эдс
- •3.2.4. Температурная зависимость сопротивления
- •3.2.5. Работа и мощность тока
- •3.2.4. Закон Джоуля-Ленца
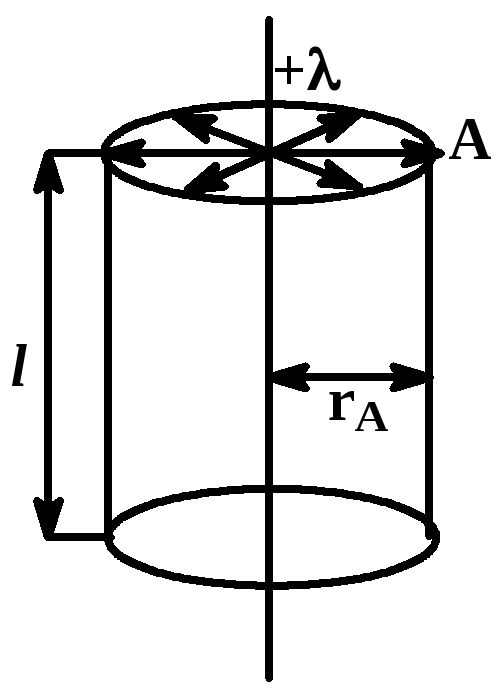
3. Поле бесконечной нити, заряженной с линейной плотностью
Линейная плотность заряда – заряд, приходящийся на единицу длины:
![]()
|
|
Для
нахождения
|
![]()
Следовательно,
![]() .
.
Разность потенциалов между точками 1 и 2 поля, лежащими на расстоянии r1 и r2 от оси цилиндра:
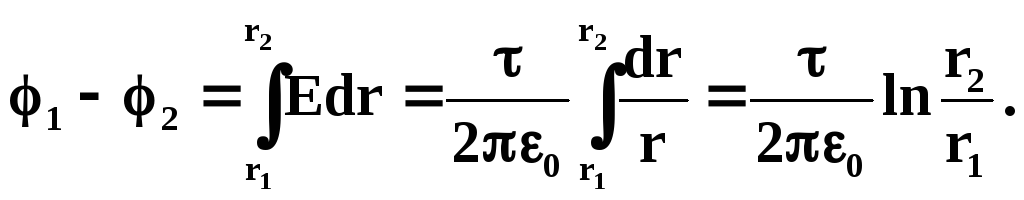
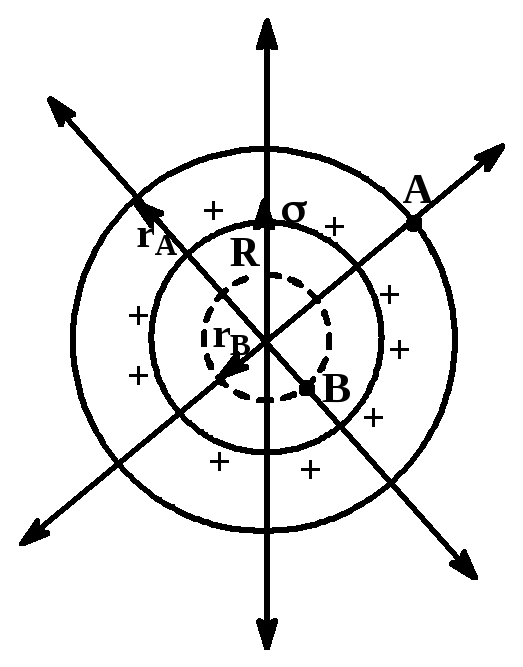
3. Поле заряженной сферической поверхности
|
|
Проводим вокруг полой металлической сферы сферическую поверхность радиусом rA. Поток вектора через эту поверхность
Тогда
|
Видно, что выражение
для
![]() получилось таким же, как и для точечного
заряда.
получилось таким же, как и для точечного
заряда.
|
|
Внутри
сферы, например в т.
B,
величина
|
Разность потенциалов
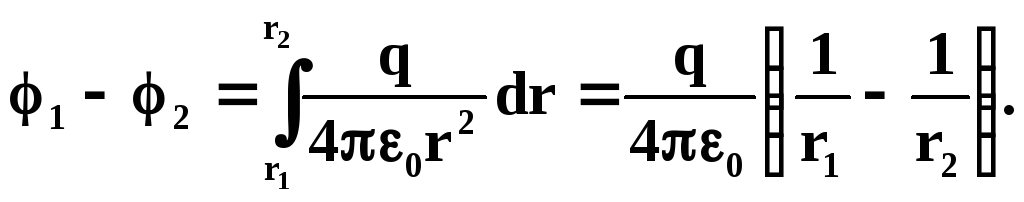
Шар, представляющий
собой диэлектрик, может быть внутри
равномерно заряжен с объемной плотностью
![]() .
Поток вектора
.
Поток вектора![]() через поверхность радиусомrR
(R
– радиус шара) равен
через поверхность радиусомrR
(R
– радиус шара) равен
![]() Заряд
внутри сферы радиусомr
равен:
Заряд
внутри сферы радиусомr
равен:
![]() .
.
По теореме Гаусса
![]() и
и
![]()
За пределами
равномерно заряженного шара выражение
для EA
будет таким
же, как и полученное нами для полой сферы
![]() ,
только величинаq
будет
равняться V:
,
только величинаq
будет
равняться V:
![]()
Разность потенциалов для точек, лежащих на расстоянии rR от центра шара:
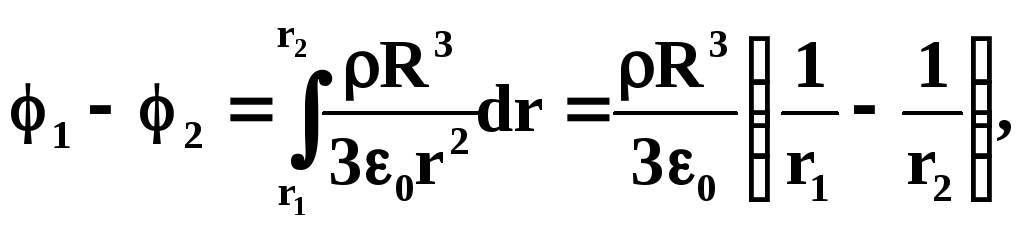
и для точек, лежащих на расстоянии rR от центра шара:
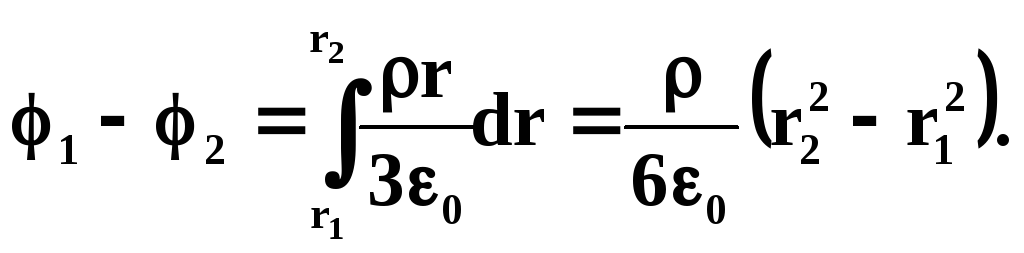
2. Проводники в электрическом поле.
Проводниками называют тела, которые хорошо проводят электрический ток, в которых есть свободные электрические заряды, способные перемещаться по всему объему проводника.
Условия равновесия зарядов на проводнике:
Напряженность поля внутри заряженного проводника должна быть равна нулю
 .
В противном случае на заряды будет
действовать электрическая сила,
вызывающая их перемещение.
.
В противном случае на заряды будет
действовать электрическая сила,
вызывающая их перемещение.Избыточные заряды располагаются на поверхности проводника. В самом деле, при
 потокФЕ вектора
потокФЕ вектора
 через любую замкнутую поверхность,
проведенную внутри проводника, равен
нулю. Из теоремы Гаусса
через любую замкнутую поверхность,
проведенную внутри проводника, равен
нулю. Из теоремы Гаусса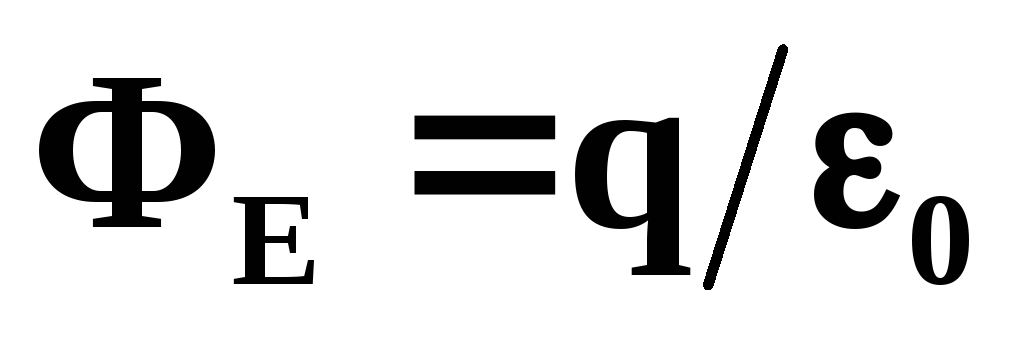 следует,
что при
следует,
что при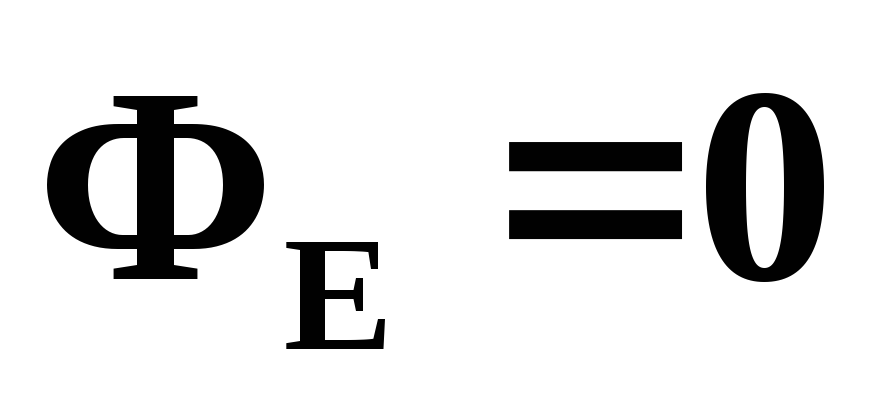 избыточный заряд внутри проводника
равен нулю:
избыточный заряд внутри проводника
равен нулю: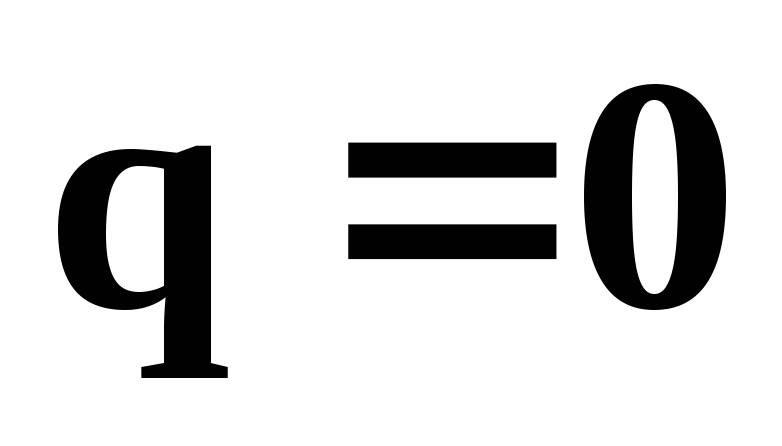 .
.Потенциал поля внутри проводника постоянен, т.к. если
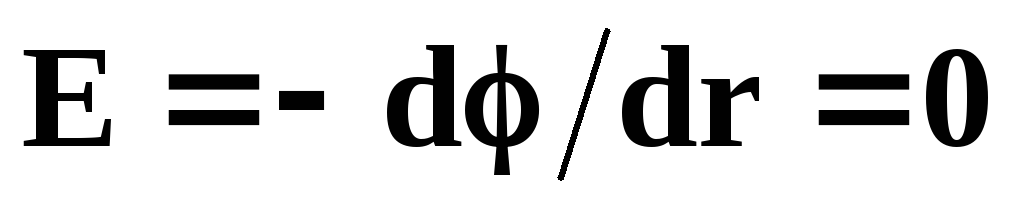 ,
то
,
то .
.В каждой точке на поверхности заряженного проводника вектор напряженности направлен по нормали к поверхности. В противном случае вектор
 можно было бы разложить на две
составляющие: нормальную к поверхности
можно было бы разложить на две
составляющие: нормальную к поверхности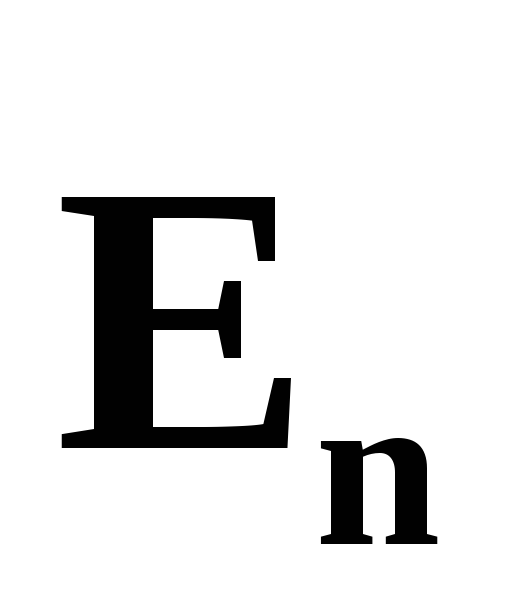 и направленную по касательной к
поверхности
и направленную по касательной к
поверхности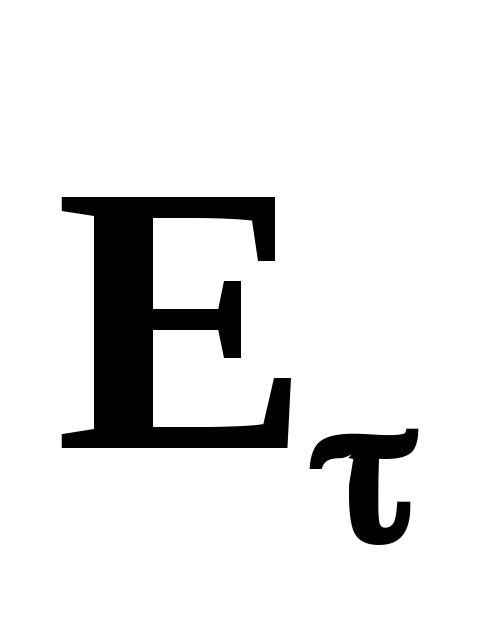 :
: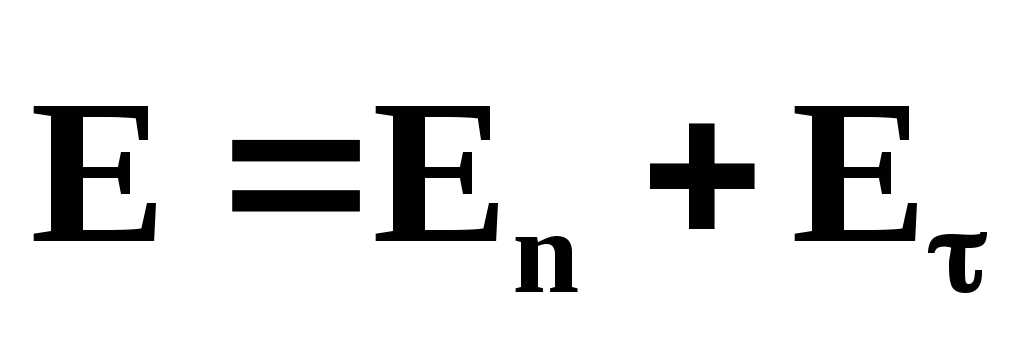 .
Если
.
Если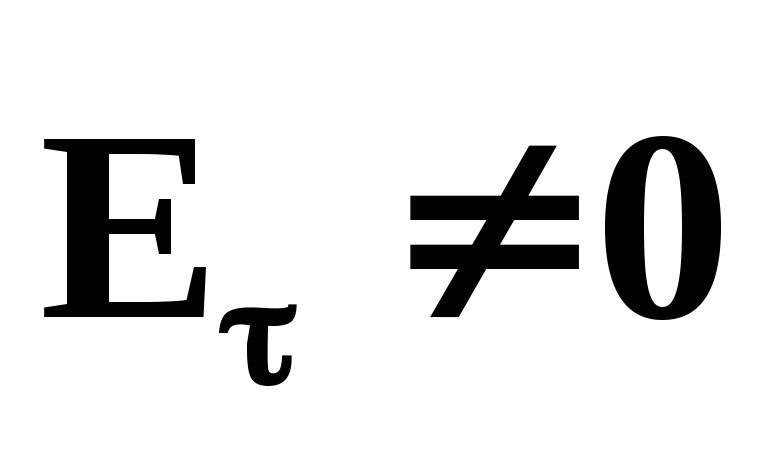 то на свободные заряды на поверхности
проводника будет действовать электрическая
сила, что заставит их перемещаться по
поверхности проводника, при этом
равновесие нарушится.
то на свободные заряды на поверхности
проводника будет действовать электрическая
сила, что заставит их перемещаться по
поверхности проводника, при этом
равновесие нарушится.Поверхность проводника является эквипотенциальной поверхностью: потенциал во всех точках на поверхности проводника одинаков и равен потенциалу внутри проводника.
|
|
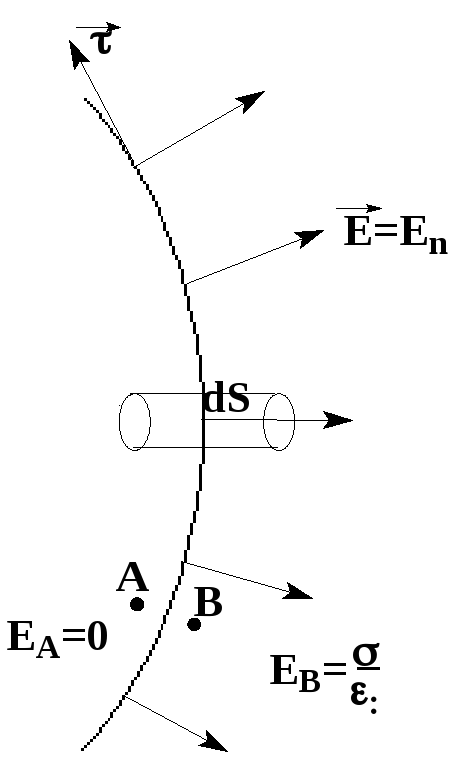
Найдем величину
E
вблизи поверхности проводника: проведем
цилиндрическую поверхность сечением
dS
с образующей, перпендикулярной
поверхности проводника и параллельной
вектору
Отсюда:
|
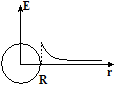
Поскольку внутри
проводника E=0,
а в непосредственной близости от
поверхности
![]() ,
то это значит, что при переходе из
проводника в пространство за проводником
(в воздух) значение
,
то это значит, что при переходе из
проводника в пространство за проводником
(в воздух) значение![]() изменяется от 0 до
изменяется от 0 до![]() .
.
Среднее значение напряженности поля на поверхности проводника получается равным:
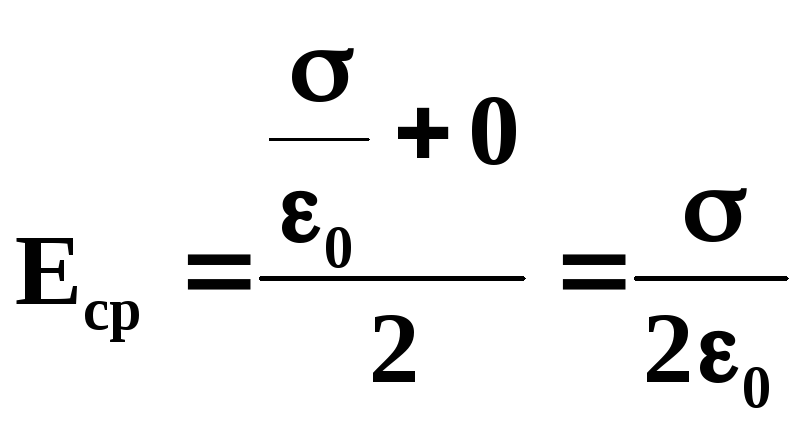
Сила, с которой поле проводника действует на заряд, расположенный на его поверхности dS, равна:
![]()
Давление, испытываемое поверхностью проводника и обусловленное избыточными зарядами на его поверхности, равно:
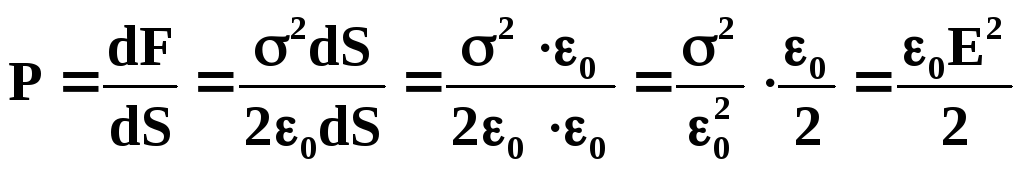
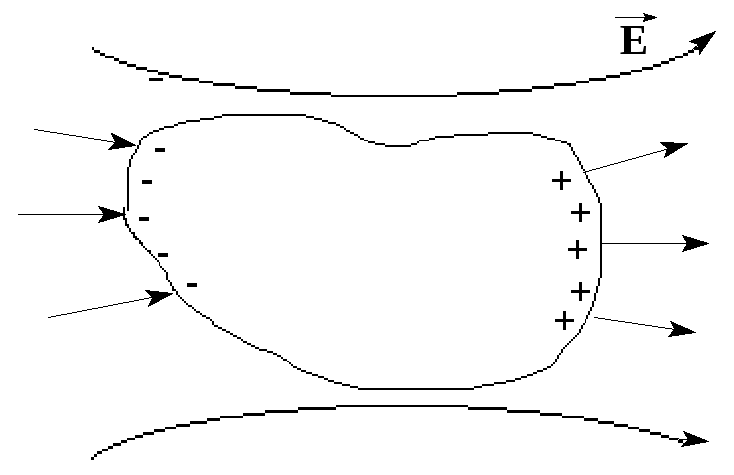
При помещении незаряженного проводника в электрическое поле имеющиеся на нем заряды приходят в движение – на противоположных поверхностях возникают избыточные электрические заряды противоположных знаков.
Возникающие на поверхности заряды создают свое поле, которое в точности равно внешнему, но противоположно по направлению – внутри проводника (в полости) поле отсутствует.
|
|
Явление возникновения электрических зарядов на поверхности проводника под действием электрического поля называется электростатической индукцией, а возникающие заряды называют индукционными. |
Перераспределение зарядов в проводнике под действием внешнего поля происходит до тех пор, пока силовые линии не окажутся перпендикулярными поверхности проводника.
Равенство нулю напряженности поля в полости проводника используют для реализации электрической защиты, причем оказалось, что электрическая защита получается достаточно хорошей не только в случае сплошной металлической оболочки, но и в случае использования мелкой металлической сетки.
Соединение проводником какого-либо тела с землей называют заземлением. При заземлении заряженных проводников, в том числе и тела человека, они теряют заряд и их потенциал будет равен потенциалу земли. Заземление корпусов приборов и аппаратов способствует их безопасной эксплуатации, т.к. исключает возможность для персонала оказаться под напряжением корпуса аппарата и земли.