- •Электростатика
- •1.1. Электрические заряды
- •1.2. Закон Кулона. Электрическое поле
- •1.3. Дальнодействие и близкодействие
- •Частица – поле – частица,
- •1.4. Напряженность электрического поля
- •1.5. Принцип суперпозиции
- •1.6. Потенциальный характер электростатического поля
- •1.7. Потенциал. Разность потенциалов
- •1.8. Графическое изображение электростатических полей
- •1.9. Связь напряженности и потенциала
- •1.10. Поток вектора напряженности электрического поля
- •1.11. Теорема Гаусса
- •1.12. Применение теоремы Гаусса
- •3. Поле бесконечной нити, заряженной с линейной плотностью
- •2. Проводники в электрическом поле.
- •2.1. Электрическая емкость.
- •2.3. Энергия электрического поля.
- •2.3.1. Энергия системы электрических зарядов.
- •2.3.2. Энергия заряженного проводника.
- •2.3.3. Энергия заряженного конденсатора.
- •2.3.4. Энергия электрического поля.
- •2.4. Диэлектрики в электрическом поле.
- •2.4.1. Поляризация диэлектриков.
- •2.4.2. Основные соотношения электростатики для поля внутри диэлектрика.
- •2.4.2.1. Вектор электрического смещения. Граница двух диэлектриков
- •3.2. Постоянный электрический ток
- •3.2.1. Сила и плотность тока
- •3.2.2. Закон Ома в интегральной и дифференциальной форме
- •3.2.3. Сторонние силы. Закон Ома для цепи, содержащей эдс
- •3.2.4. Температурная зависимость сопротивления
- •3.2.5. Работа и мощность тока
- •3.2.4. Закон Джоуля-Ленца
1.12. Применение теоремы Гаусса
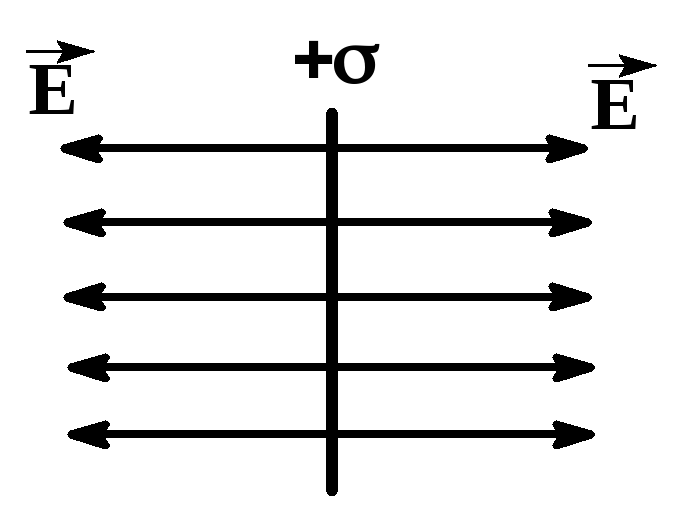
1. Поле бесконечной равномерно заряженной плоскости
Величину заряда, приходящуюся на единицу поверхности, называют поверхностной плотностью заряда :
![]()
|
|
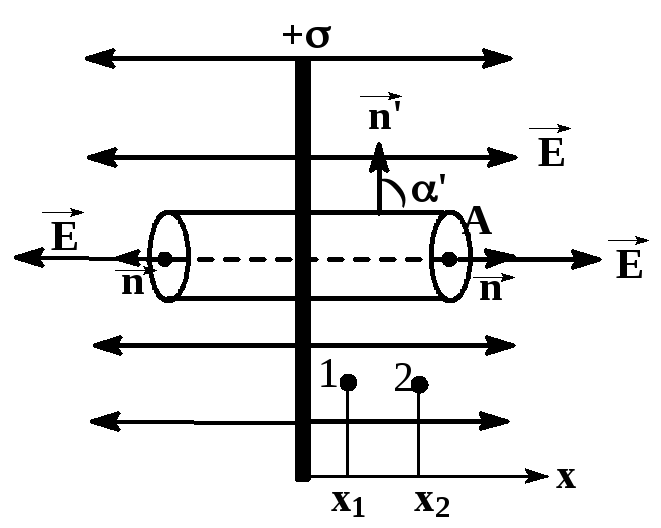
Пусть плоскость заряжена положительно с поверхностной плотностью заряда +=const. Из соображений симметрии силовые линии имеют вид прямых, перпендикулярных плоскости и выходящих из положительных зарядов . |
Найдем напряженность в точке A.
|
|
В
соответствии с законом Кулона для
нахождения величины
|
Поверхность
обычно берут такой, чтобы максимально
просто можно было бы вычислить ее
площадь. В случае заряженной плоскости
этой поверхностью является цилиндрическая,
у которой образующая перпендикулярна
плоскости. Поскольку линии
![]() перпендикулярны заряженной плоскости
и угол
между вектором
перпендикулярны заряженной плоскости
и угол
между вектором
![]() и нормалью к основаниям цилиндра равен
нулю, следовательно,cos=1.
Для боковой же поверхности
и нормалью к основаниям цилиндра равен
нулю, следовательно,cos=1.
Для боковой же поверхности
![]() .
Угол’=90,
следовательно, cos=0
и
.
Угол’=90,
следовательно, cos=0
и
![]() .
.
Итак, общий поток
вектора
![]() через замкнутую цилиндрическую
поверхность
через замкнутую цилиндрическую
поверхность![]() равен сумме потоков через два основания
равен сумме потоков через два основания![]() и
и![]() и потоку через боковую поверхность
и потоку через боковую поверхность![]() :
:
![]() где
где
![]() - берем элементарные площадки одинаковой
величины.
- берем элементарные площадки одинаковой
величины.
Суммарный заряд внутри цилиндра
![]() .
.
Тогда по теореме Гаусса запишем:
![]()
и получаем:
![]()
Найдем разность
потенциалов поля между точками 1
и 2
на расстоянии x1
и x2
от плоскости. Воспользуемся соотношением
![]() .
Векторы напряженности
.
Векторы напряженности![]() направлены по осиOx,
поэтому:
направлены по осиOx,
поэтому:
![]()
![]()
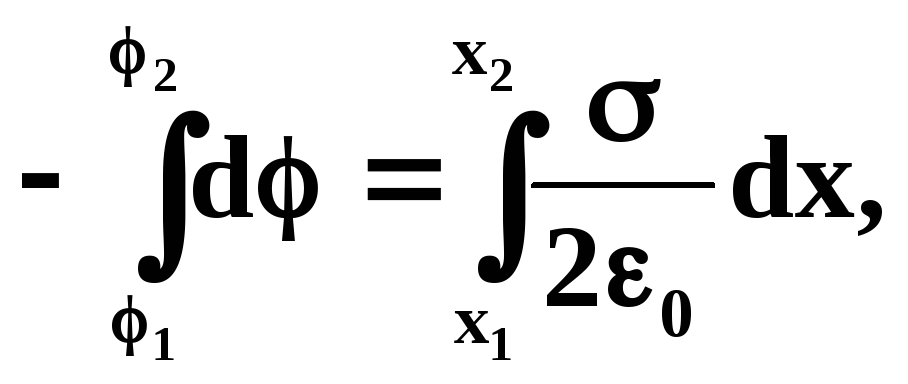
откуда получим:
![]()
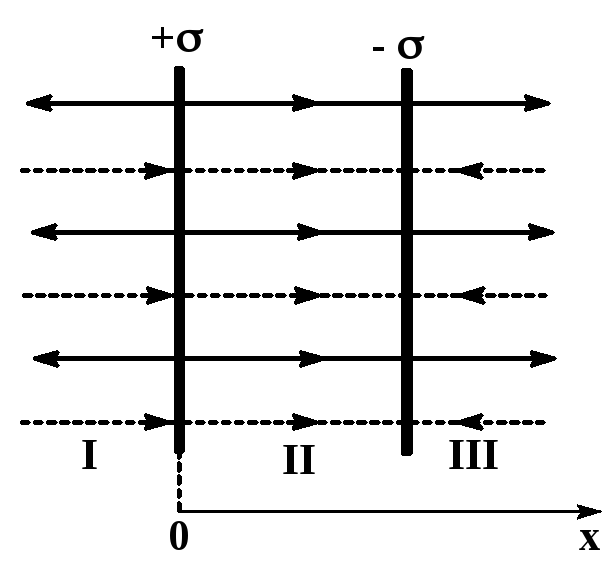
2. Поле двух параллельных бесконечных равномерно заряженных плоскостей
|
|
Для рассматриваемого случая воспользуемся принципом суперпозиции электрических полей. Изобразим линии напряженности положительно заряженной плоскости сплошными линиями, отрицательно заряженной плоскости – пунктирными. Укажем направление силовых линий в областях I, II и III. |
Результирующая напряженность в каждой области по принципу суперпозиции:
![]()
Напряженности, создаваемые каждой плоскостью в отдельности:
![]() и
и
![]() .
.
Из рис. видно, что
в области II
векторы
![]() и
и![]() сонапралены
и при
сонапралены
и при![]()
![]()
В областях I
и III
векторы
![]() и
и![]() направлены противоположно друг другу,
т.е.
направлены противоположно друг другу,
т.е.![]() и
и![]() .
.
Найдем разность потенциалов между плоскостями. Обозначим расстояние между ними d и воспользуемся соотношением:
![]()
![]()
Интегрируя
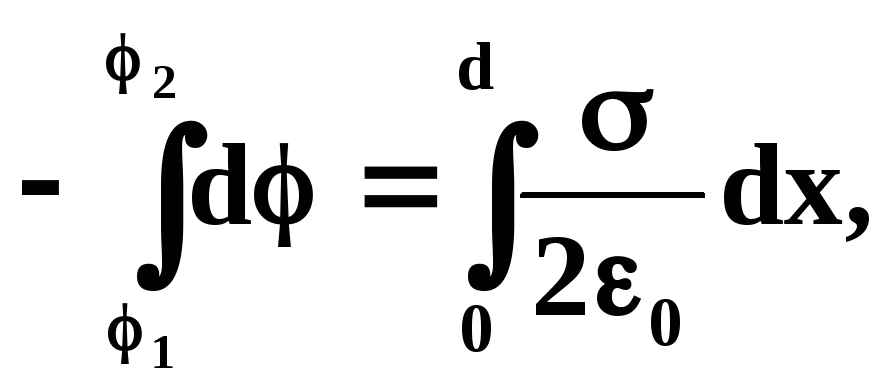
получим
![]()