1.10. Поток вектора напряженности электрического поля

Рассмотрим два случая:

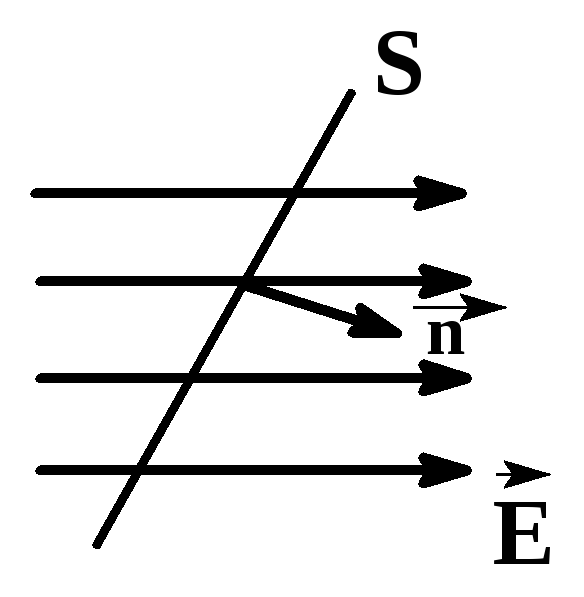
1. Электростатическое поле однородное, поверхность S плоская .

Величина ФЕ, равная скалярному произведению векторов и, называетсяпотоком вектора через площадкуS: где  - угол между векторами и.

Вектор равент.е. модуль вектораравен величине площадки, а направление совпадает с направлением нормалик ней.

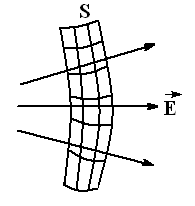
2. Поле неоднородное, поверхность S неплоская.

Поверхность S делим на элементарные площадки, которые можно считать плоскими, а поле в их пределах однородным. Тогда Полный поток Поток ФЕ – величина скалярная, в зависимости от угла  он может быть положительным или отрицательным.

Знак величины потока зависит от выбора направления нормали к поверхности, его выбор является условным. Для замкнутой поверхности условились считать положительной внешнюю нормаль к поверхности. Это значит, что Ф_Е<0 на тех участках замкнутой поверхности, в которые силовые линии входят, и Ф_Е>0 на тех участках, из которых силовые линии выходят. Потоку Ф_Е можно дать геометрическую интерпретацию: поток вектора через некоторую поверхностьS равен числу силовых линий, пронизывающих эту поверхность: Ф_Е=N.

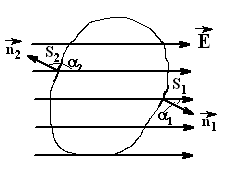
ФЕ10, т.к. 1/2, cos10. ФЕ20, т.к. 2/2, cos10.

Поток вектора через замкнутую поверхность

1.11. Теорема Гаусса

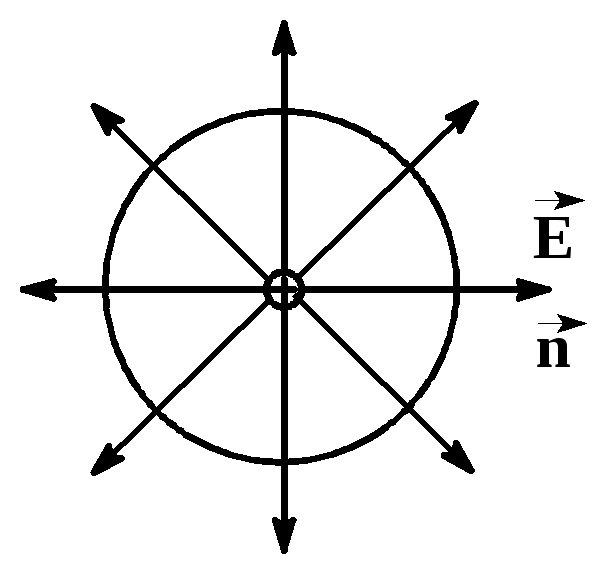
Рассмотрим поле единичного положительного заряда q.

Окружим заряд сферической поверхностью радиуса r. Поток ФЕ через эту поверхность равен: 1) Во всех точках поверхности т.к. r = const для всех точек среды.

2)  = 0, cos = 1. Тогда

Окружим заряд произвольной поверхностью: сколько силовых линий пронизывает сферическую поверхность, столько же их пронизывает произвольную поверхность, т.е. для произвольной поверхности

Если внутри поверхности находится несколько точечных зарядов, то и

Теорема Гаусса: поток вектора через произвольную замкнутую поверхность, охватывающую заряд, равен величине этого заряда, деленной на электрическую постоянную₀.

Рассмотрим случай, когда заряды находятся вне замкнутой поверхности.

Каждая силовая линия пересекает поверхность дважды: один раз она входит в поверхность, второй – выходит из нее. Поэтому

где Ф_Е1 – поток, образуемый входящими линиями (Ф_Е10, т.к. ₁90 и cos₁1); Ф_Е2 – поток, образуемый выходящими линиями (Ф_Е20, т.к. ₁90 и cos₁1).

Так как тоФ_Е = 0, т.е. вне замкнутой поверхности поток вектора равен нулю.

Теорема Гаусса позволяет рассчитывать и электростатических полей и в этом смысле эквивалентна закону Кулона. Оба эти закона устанавливают связь зарядов как источников поля с самими характеристиками поля.