1.3. Дальнодействие и близкодействие

Концепция электрического поля как самостоятельной физической реальности неразрывно связана с решением проблемы о взаимодействии материальных объектов, выступающей в виде теории дальнодействия и близкодействия.

Первоначально предполагалось, что электрические силы, как и силы всемирного тяготения, представляют собой «действия на расстоянии без какой-либо промежуточной среды (концепция дальнодействия)».

Введение понятия «электрическое поле» позволяет представить взаимодействие заряженных частиц в виде схемы:

Частица – поле – частица,

т.е. одна частица создает в окружающем пространстве электрическое поле, которое действует на другую заряженную частицу.

С введением понятия поля место мгновенного дальнодействия заняло передающееся с конечной скоростью действие от точки к ближайшей точке в непосредственно следующие друг за другом моменты времени (концепция близкодействия).

Однако в электростатике обе концепции равноправны в смысле физических выводов, но равноправие исчезает при переходе к электродинамике. Объясняется это тем, что в электростатике электрическое поле неотделимо от заряда. Если ликвидировать заряд, то с точки зрения теории дальнодействия мгновенно исчезает во всем пространстве привязанное к этому заряду электростатическое поле. Электромагнитное поле может отрываться от заряда, существовать самостоятельно и распространяться в пространстве.

Таким образом, решение проблемы взаимодействия заряженных материальных объектов представляется как противоречивое единство двух противоположных концепций: дально- и близкодействия.

1.4. Напряженность электрического поля

Напряженностью электрического поля в данной точке называется вектор, численно равный силе, действующей на единичный положительный заряд, помещенный в данную точку поля:

За единицу напряженности принимается напряженность в такой точке поля, в которой на единичный заряд действует единичная сила:

В случае точечного заряда

\

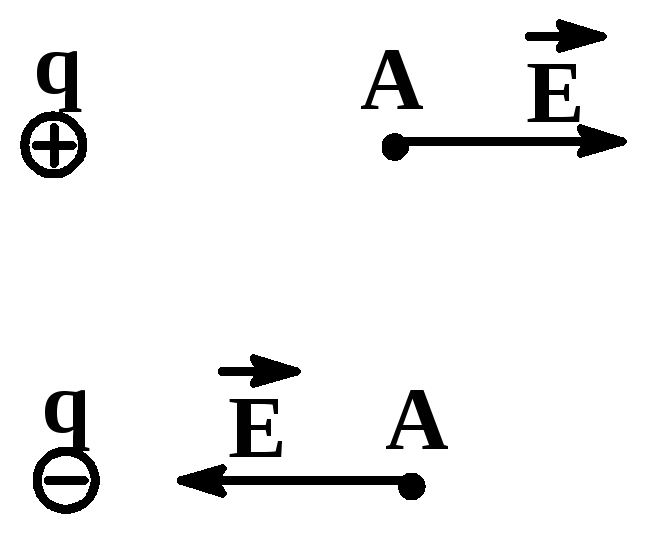
Найдем направление напряженности в точке A поля, создаваемого точечным зарядом q. Направление совпадает по направлению с силой, действующей на положительный зарядq0. Эта сила направлена по линии, соединяющей заряды.

1.5. Принцип суперпозиции

а) Дискретное распределение зарядов

Пусть поле создано системой точечных зарядов q₁, q₂, ..., q_n. Воспользуемся законом независимости действия сил: результирующая сила, действующая на заряд q₀, помещенный в точку A, будет равна геометрической сумме сил , действующих на него со стороны каждого из зарядовq_i:

Разделим на q₀:

или

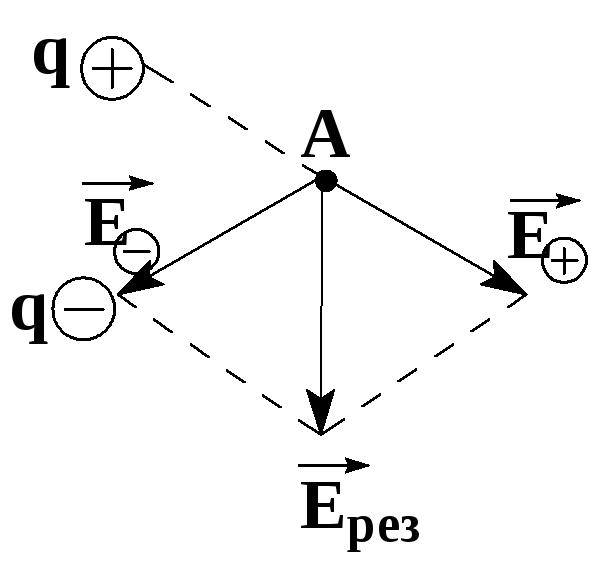
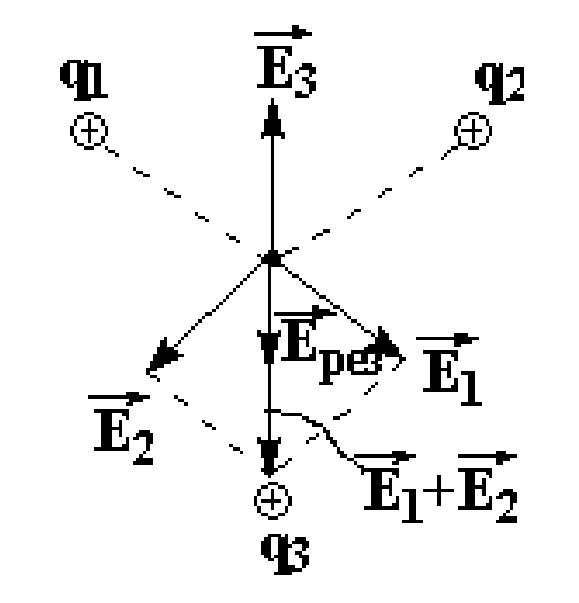
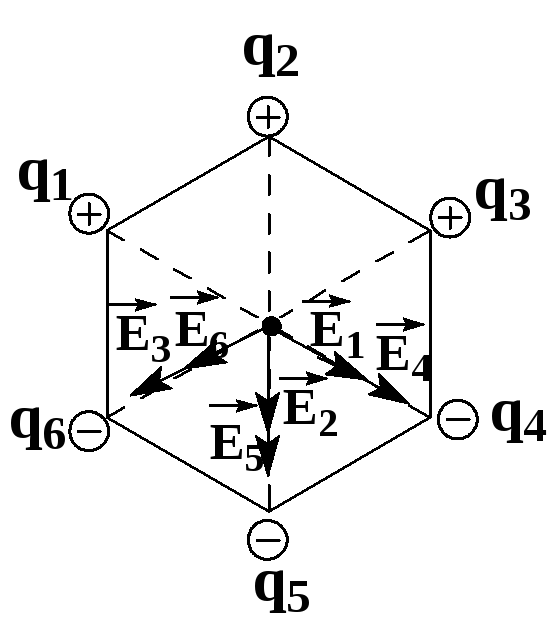
Последнее выражение – принцип суперпозиции электрических полей:

Если поле создано несколькими зарядами, то результирующая напряженность поля есть векторная сумма напряженностей полей, созданных каждым зарядом в отдельности.

б) Непрерывное распределение зарядов

На практике электрические поля, как правило, создаются заряженными телами. В этом случае принцип суперпозиции имеет вид:

где V – объем заряженного тела.