3.2.2. Закон Ома в интегральной и дифференциальной форме

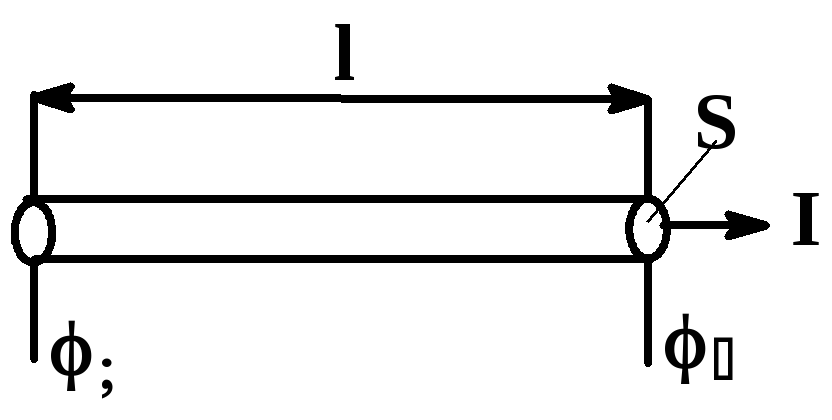
Пусть по проводнику длиной l и сечением S течет ток I. В проводнике создается электрическое поле напряженности E, а 1 и 2 – потенциалы на концах проводника. В случае однородного проводника величину 1 - 2 = U можно назвать падением напряжения на участке проводника.

Закон Ома: сила тока, текущего по однородному участку проводника, прямо пропорциональна падению напряжения на проводнике:

- закон Ома в интегральной форме

где R – электрическое сопротивление проводника.

Размерность сопротивления в СИ: [R] = В/А = Ом.

Ом – сопротивление такого проводника, в котором при напряжении в 1 В течет ток 1А.

Сопротивление зависит от геометрических размеров и формы проводников, материала и температуры проводников. Для цилиндрического проводника

где  - удельное сопротивление проводника.

Удельное сопротивление численно равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м². Размерность удельного сопротивления в СИ: [] = Омм.

Величина, обратная сопротивлению, называется проводимостью.

Величина, обратная удельному сопротивлению, называется удельной проводимостью:

Единица, обратная Ом, называется Сименсом [См].

Учитывая выше написанные уравнения, а также , получим:

– закон Ома в дифференциальной форме.

3.2.3. Сторонние силы. Закон Ома для цепи, содержащей эдс

Для возникновения и существования электрического тока необходимо:

1. наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно;

2. наличие электрического поля, энергия которого должна каким-то образом восполняться.

Соединим проводником два тела с зарядами +q и –q. Кулоновские силы заставляют электроны перемещаться по проводнику. Возникнет ток. Однако тела при этом будут разряжаться, разность потенциалов уменьшится, ток быстро прекратится.

Т.е. если в цепи действуют только силы электростатического поля, то происходит перемещение носителей таким образом, что потенциалы всех точек цепи выравниваются и электростатическое поле исчезает.

Следовательно, поле кулоновских сил не может являться причиной постоянного электрического тока.

Ток в проводнике нейтрализует заряды на его концах. Для поддержания постоянного тока необходимо поддерживать постоянную разность потенциалов, следовательно, разделять заряды. Электрические силы разделять заряды не могут.

Силы, разделяющие заряды, имеют неэлектрическую природу и называются сторонними силами.

Устройство, в котором действуют сторонние силы, называется источником тока.

Сторонние силы заставляют заряды двигаться внутри источника тока против сил поля. Благодаря этому в цепи поддерживается постоянная разность потенциалов.

Перемещая заряды, сторонние силы совершают работу за счет энергии, затраченной в источнике тока. Например, в электрофорной машине разделение зарядов происходит за счет механической работы, в гальваническом элементе – за счет энергии химических реакций и т.д.

Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС).

Обозначим - вектор напряженности поля сторонних сил.

Результирующее поле, действующее на заряды в проводнике, в общем случае

Плотность тока в цепи

.

– закон Ома в дифференциальной форме для цепи, содержащей ЭДС.

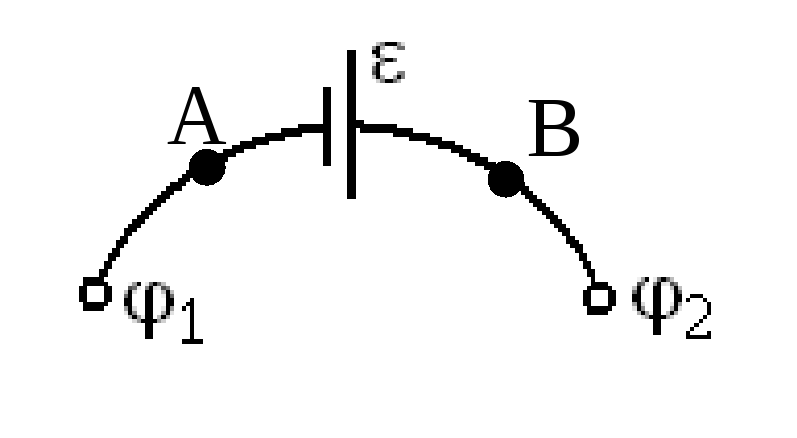
Рассмотрим участок AB замкнутой цепи, содержащей ЭДС (рис.3.18). Выделим мысленно малый элемент dl.

Плотность тока на этом участке опишется уравнением . Умножим скалярно обе части этого равенства наи проинтегрируем по участкуAB:

Рассмотрим каждый интеграл в отдельности:

а)

где _А - _В – разность потенциалов между точками A и B.

Разность потенциалов численно равна работе кулоновских сил по перемещению единичного положительного заряда из т.A в т.B;

б)

где  - ЭДС.

ЭДС, действующая на участке цепи, численно равна работе сторонних сил по перемещению единичного положительного заряда из т.A в т.B;

в)

где R_AB – сопротивление участка AB.

С учетом выше сказанного можно получить:

- закон Ома для участка цепи с ЭДС.

Частные случаи:

1. если на данном участке цепи источник тока отсутствует, то получаем закон Ома для однородного участка цепи:

2. если цепь замкнута (=0), то получим закон Ома для замкнутой цепи:

где  - ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи, r_внутр – внутреннее сопротивление источника тока, R_внеш – сопротивление внешней цепи;

3. если цепь разомкнута, то I = 0 и ₁₂ = ₂ - ₁, т.е. ЭДС, действующая в разомкнутой цепи равна разности потенциалов на ее концах.

4. В случае короткого замыкания сопротивление внешней цепи R_внеш = 0 и сил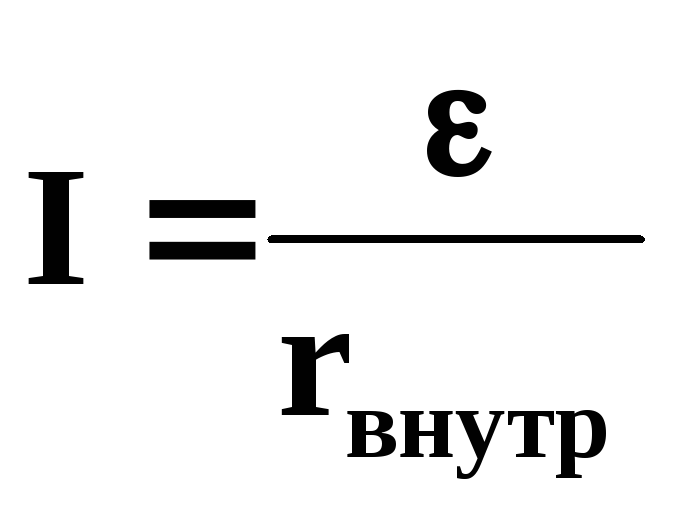а тока в этом случае ограничивается только величиной внутреннего сопротивления источника тока.

Величина IR_AB = U_AB называется падением напряжения на участке AB.

Падение напряжения на участке AB численно равно работе кулоновских и сторонних сил по перемещению единичного положительного заряда из т.A в т.B.

Если цепь замкнута, то ₁ = ₂ и

– закон Ома для замкнутой цепи.

Если участок цепи не содержит ЭДС, то