2.4.2.1. Вектор электрического смещения. Граница двух диэлектриков
Источником электростатического поля являются свободные и связанные электрические заряды: линии напряженности начинаются на положительных зарядах (или в бесконечности) и оканчиваются на отрицательных (или в бесконечности).
Однако при решении
задач, связанных с электрическим полем
в диэлектрике, в ряде случае оказывается
более удобным учитывать только поле
свободных зарядов. Для этого вводится
понятие вектора электрического смещения
(
).
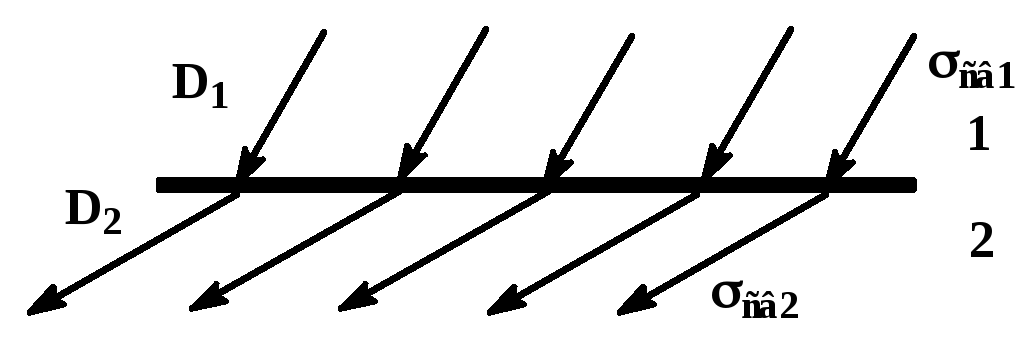
Рассмотрим изменение электрического поля на достаточно протяженной границе двух однородных и однородно поляризованных диэлектриков 1 и 2.
|
|
В
первом диэлектрике напряженность
электрического поля и вектор поляризации
соответственно равны
|
и
,
во втором диэлектрике -
и
.В общем случае все эти четыре вектора произвольно ориентированы в диэлектриках, поэтому можно говорить об их тангенциальных к границе раздела (E1, E2 и P1, P2) и нормальных (En1, En2 и Pn1, Pn2) составляющих.
На границе возникнут связанные электрические заряды противоположных знаков, поверхностные плотности которых равны св1 и св2. Эти заряды создадут электрическое поле E’. Напряженность E’ уменьшит нормальную составляющую напряженности в одном диэлектрике и увеличит в другом, поэтому E’ будет определяться разностью нормальных составляющих напряженности:
Это уравнение можно записать так:
или:
Отсюда видно, что на границе двух диэлектриков сохраняется нормальная составляющая:
некоторого вектора:
Это и есть вектор электрического смещения.
Т.е. можно говорить о линиях электрического смещения и о потоке вектора электрического смещения через некоторую поверхность.
Поток вектора электрического смещения не изменятся на границе двух диэлектриков, т.е. линии этого вектора не начинаются и не заканчиваются на связанных зарядах, а линии напряженности поля начинаются и заканчиваются на связанных зарядах.
Из приведенных соотношений видно,
Внутри диэлектрика
,
в вакууме
.
Видно, что величина Dn остается постоянной при переходе из вакуума в среду, а величина En изменяется.
Или в векторной форме:
Запишем для нашего случая теорему Гаусса. Общий заряд в диэлектрике qобщ можно найти как разность свободных зарядов и связанных зарядов.
Сумма
взята со знаком минус потому, что поле
связанных зарядов направлено противоположно
полю свободных зарядов.
Получаем:
–теорема
Гаусса для поля внутри диэлектрика:
поток вектора
электрического смещения сквозь замкнутую
поверхность равен алгебраической сумме
свободных зарядов, находящихся внутри
этой поверхности:
Запишем в виде:
отсюда получаем:
Величина поля внутри диэлектрика:
или:
В других конкретных случаях соотношения для электростатического поля с диэлектриком имеют другой вид и чаще всего значительно более сложный, нежели полученные нами для плоской пластины внутри конденсатора. В частности, в некоторых случаях введение диэлектрика сопровождается не только ослаблением поля, но и его усилением.
|
|
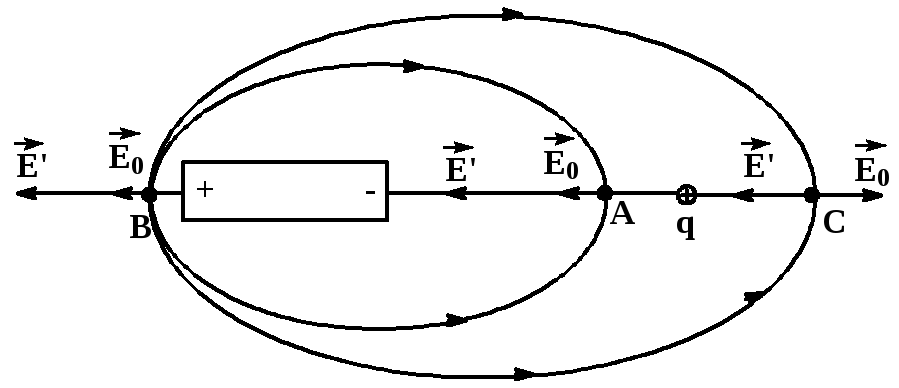
Поле, созданное зарядом q в т. A и B, по направлению совпадает с полем связанных зарядов диэлектрика M, внесенного в поле заряда q. |
В т. C величины E0 и E’ направлены в противоположные стороны, т.е. в этой точке внесение диэлектрика сопровождается ослаблением поля.
Напряженность электрического поля точечного заряда q в диэлектрике выражается формулой:
Получаем выражение для электрического смещения поля точечного заряда:
Как видно, электрическое смещение в однородном изотропном диэлектрике не зависит от свойств вещества.