
- •Введение
- •Понятие об экономико-математических методах и моделях
- •1.1.Определение модели и цели моделирования
- •1.2. Последовательность построения экономико-математической модели
- •1.3. Классификация экономико-математических методов
- •1.4. Классификация экономико-математических моделей
- •1.5. Объекты моделирования
- •1.6. Цель, критерий и ограничения в экономико-математических моделях
- •2. Математические модели рынка
- •2.1. Понятие рыночного равновесия
- •2.2. Паутинообразная модель рынка
- •2.3. Существование и единственность рыночного равновесия
- •2.4. Государственное регулирование рынка. Налоги
- •. Дотации
- •2.6. Фиксированные цены
- •2.7. Оценка прибыли и убытков при государственном регулировании рынка
- •2.8. Поддержание стабильных цен и производственные квоты
- •2.9. Принципы ценообразования в рыночной экономике. Диверсификация цен
- •2.9.1. Диверсификация цен в зависимости от дохода покупателя
- •2.9.2. Диверсификация цен в зависимости от объема потребления
- •2.9.3. Диверсификация цен по категориям товаров
- •Совокупная прибыль
- •2.9.4. Диверсификация цен по времени
- •3. Производственные функции
- •3.1. Виды производственных функций
- •3.2. Функция Кобба-Дугласа
- •3.3. Модель Солоу
- •3.4. Модель Стоуна
- •3.5. Двойственная задача потребительского выбора
- •3.6. Функция спроса Маршалла
- •3.7. Модель общего равновесия Вальраса
- •3.8. Рыночное равновесие в модели Леонтьева
- •3.9. Пример построения производственной функции
- •Значения коэффициентов парной корреляции
- •3.10. Производственные функции и прогнозирование
- •4. Модели оптимального планирования
- •4.1. Оптимизация прибыли предприятия
- •Исходные данные для предельного анализа
- •4.2. Оптимизация прибыли методами математического программирования
- •Исходные данные для решения задачи оптимизации
- •4.3. Оптимизация прибыли при ограничениях на используемые ресурсы
- •Исходные данные по изделиям
- •Результаты расчета Таблица 4.8
- •4.4. Планирование оптимальной мощности строительного предприятия
- •Для решения задачи на пк коэффициенты целевой функции, матрицы ограничений и правые части ограничений необходимо записать в виде симплекс-матрицы (табл.4.10).
- •Оптимальное значение целевой функции – 240,000.
- •4.5. Модели стохастического программирования
- •4.6. Модели оптимального планирования транспортного типа
- •4.7. Решение задач по планированию перевозок
- •4.8. Производственно-транспортные модели
- •4.9. Транспортные модели с промежуточными пунктами
- •4.10. Модели параметрического программирования
- •4.11. Модель распределения инвестиционных ресурсов между строительными организациями, прошедшими конкурсный отбор
- •4.12. Производственно-транспортная задача прикрепления источников теплоснабжения к потребителям продукции
- •5. Матричные игры
- •5.1. Классификация матричных игр
- •5.2. Игры с нулевой суммой
- •5.3. Решение игры в чистых стратегиях
- •5.4. Решение игры в смешанных стратегиях
- •Очевидным следствием из теоремы о минимаксе является соотношение
- •5.5. Игры с ненулевой суммой и кооперативные игры
- •5.6. Введение в теорию игр п лиц
- •5.7. Позиционные игры
- •5.8. Выбор оптимальной стратегии в условиях неопределенности (игры с природой)
- •5.8.1. Специфика ситуации полной неопределенности
- •5.8.2. Критерии выбора оптимальной стратегии
- •5.9. Применение теории матричных игр в управлении
- •5.10. Сведение матричной игры к задаче линейного программирования Рассмотрим игру, платежная матрица которой имеет размерность
- •5.11. Решение игры с применением процессора электронных таблиц
- •5.12. Определение победителя подрядных торгов с применением теории игр
- •6. Имитационное моделирование
- •6.1. Метод Монте-Карло
- •7. Моделирование систем массового обслуживания
- •7.1. Одноканальная модель с пуассоновским входным потоком с экспоненциальным распределением длительности обслуживания
- •7.2. Многоканальная модель с пуассоновским входным потоком и экспоненциальным распределением длительности обслуживания
- •8. Модели оценки эффективности инвестиционных проектов
- •8.1. Расчет абсолютных и относительных показателей эффективности проекта
- •8.2. Применение процессоров электронных таблиц для оценки эффективности инвестиций
- •8.3. Оптимальное планирование портфеля инвестиций
- •8.4. Учет факторов риска при оценке инвестиций
- •8.5. Определение уровня недиверсифицируемого риска методом корреляционно-регрессионного анализа
- •Исходные данные для расчета
- •9. Модели оценки финансового состояния предприятия
- •9.1. Виды моделей
- •9.2. Статическая и динамическая модели оценки финансового
- •Коэффициенты рентабельности
- •Оценка деловой активности
- •Оценка финансовой устойчивости
- •Оценка платежеспособности и ликвидности
- •Рекомендуемые значения оцениваемых показателей
- •Вопросы и задания
- •Заключение
- •Библиографический список
- •Экономико-математические методы и модели
- •394006 Г.Воронеж, ул. 20-летия Октября, 84
3.3. Модель Солоу
Модель Роберта Солоу [5, 6] была построена на неоклассической предпосылке господства совершенной конкуренции на рынках факторов производства, обеспечивающей полную занятость ресурсов. Ученый исходил из того, что необходимым условием является равенство совокупного спроса и совокупного предложения. При этом совокупное предложение в его модели определялось на основании производственной функции Кобба-Дугласа, выражающей отношение функциональной зависимости между объемом производства с одной стороны и используемыми факторами и их взаимной комбинацией — с другой.
Целью модели Солоу является ответ на вопросы: каковы факторы сбалансированного экономического роста, какой темп роста может позволить себе экономика при заданных параметрах экономической системы и как при этом максимизируются доходы населения и объем потребления?
В общем виде объем национального выпуска Y является функцией 3-х факторов производства: труда L, капитала K, земли N:
Y = f (L, K, N).
Фактор земли в модели Солоу был опущен ввиду малой эффективности в экономических системах, характеризующихся высоким технологическим уровнем, и поэтому объем выпуска зависит от трудовых и производственных факторов Y = f (L, K).
В развернутом виде эта формула имеет вид:
Y = ( Y / L) L (Y / K) K, (3.31)
где Y / L – предельный продукт труда MPL, Y / K – предельный продукт капитала MPK.
Это значит, что общий продукт равняется сумме произведений затраченного количества труда и капитала на их предельные продукты, т.е. на прирост продуктов Y от увеличения затрат труда L и затрат капитала K. В упрощенном виде y = Y / L, где y – производительность труда; k = K/ L, где k — капиталовооруженность труда. Тогда производственная функция имеет вид y= f (k), где f (k) = F (k,1).
Графическое изображение этой функции имеет вид, показанный на рис. 3.1. Рисунок показывает, что капиталовооруженность k определяет размер выпуска продукции на одного работника: y = f (k).

Рис. 3.1. График производственной функции в модели Солоу
При этом tg = MPK: если k увеличивается на одну единицу, то y возрастает на МРК единиц. По мере роста капиталовооруженности труда его производительность увеличивается, но с убывающей скоростью, т.к. МРК снижается.
Совокупный спрос в модели Солоу определяется инвестиционным и потребительским спросом. Уравнение выпуска продукции на одного работника имеет вид
= с + i, (3.32)
где с и i – потребление и инвестиции.
Доход делится между потреблением и сбережениями в соответствии с нормой сбережения, так что потребление можно представить как
с = (1 — s) y, (3.33)
где s — норма сбережения (накопления).
Тогда у = с + i = (1— s) y + i, откуда i = sy. В условиях равновесия инвестиции равны сбережениям и пропорциональны доходу.
В результате условие равенства спроса и предложения может быть представлено как
f (k) = c + i или f (k) = i / s.
Производственная функция определяет предложение на рынке товаров, а накопление капитала – спрос на производственную продукцию. Объем же капитала меняется под воздействием инвестиции выбытия. Инвестиции в расчете на одного работника являются частью дохода, приходящегося на одного работника (i = sy) или
i = s * f(k). (3.34)
Из
этого следует, что, чем выше уровень
капиталовооруженности k,
тем выше уровень производства f(k)
и больше инвестиции i.
В модели Р.Солоу норма сбережений – ключевой фактор, определяющий уровень устойчивости капиталовооруженности. Более высокая норма сбережений обеспечивает больший запас капитала и более высокий уровень производства.
Другим фактором непрерывного экономического роста в условиях устойчивой экономики является рост населения. Для устойчивости экономики необходимо, чтобы инвестиции sf(k) компенсировали последствия выбытия капитала и рост капитала (d + n) k, на графике точка Е (рис. 3.2). Однако если рост населения не сопровождается увеличением инвестиций, то это ведет к уменьшению запаса капитала на одного работника.
Таким образом, если страны с более высокими темпами роста населения имеют меньшую капиталовооруженность, то значит – и более низкие доходы.

Рис. 3.2. Инвестиции s f(k) и рост капитала (d + n)k
Третьим источником экономического роста после инвестиций и увеличения численности населения является технический прогресс. В неоклассической теории технический прогресс — это качественные изменения в производстве (повышение образования работников, улучшение организации труда, рост масштабов производства) [10].
Включение в модель технического прогресса изменит исходную производственную функцию: Y = f(K, L, ), где — эффективность труда одного работника (зависит от здоровья, образования, квалификации), L – численность эффективных единиц рабочей силы.
Технический прогресс вызывает прирост эффективности с постоянным темпом g. Если g = 5%, то отдача от каждой единицы труда увеличиться на 5 % в год, а это равносильно тому, что объем производства возрастает так, как если бы рабочая сила за год выросла на 5 %. Это трудосберегающая форма технического прогресса.
Если же численность занятых L растет с темпом n, а эффективность растет с темпом g, то L будет увеличиваться с темпом n + g. Капитал на единицу труда с постоянной эффективностью составит k1 + [K /(L)], а объем производства на единицу труда с постоянной эффективностью y1 = Y / (L). Состояние устойчивого равновесия достигается при условии
s x f(k1) = (d + n + g) x k1,
где d — норма амортизации.
Из вышеприведенного равенства следует, что существует лишь один уровень капиталовооруженности k1, при которой капитал и выпуск продукции, приходящиеся на единицу труда с неизменной эффективностью, постоянны (рис. 3.3).
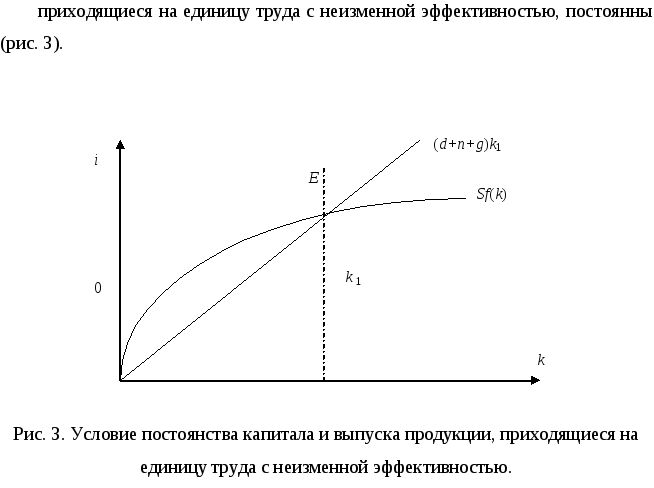
Рис. 3.3. Условие постоянства капитала и выпуска продукции, приходящиеся на единицу труда с неизменной эффективностью
В устойчивом состоянии k1 при наличии технического прогресса общий объем капитала К и выпуск Y будет расти с темпом n + g. В расчете на одного работника капиталовооруженность k/L и выпуск Y/L будет расти с темпом g. Таким образом, технический прогресс в модели Солоу — это единственное условие непрерывного экономического развития [10].
