
- •Министерство образования Республики Беларусь
- •Содержание
- •Введение
- •Общие методические указания
- •1 Краткие сведения из теории
- •1.1 Структурный анализ плоских механизмов
- •1.2 Кинематический анализ механизмов
- •1.3 Динамический анализ механизмов
- •2 Образец выполнения расчета структурного, кинематического и динамического анализа механизма
- •2.1 Задание на расчет и исходные данные
- •2.2 Структурный анализ механизма
- •2.3 Построение плана положений механизма
- •2.4 Определение скорости и ускорения ползуна при помощи кинематических диаграмм
- •2.5 Применение планов скоростей и ускорений для кинематического анализа механизмов
- •2.6 Определение сил, приложенных к звеньям механизма
- •2.7 Расчет реакций в кинематических парах и величины уравновешивающей силы методом планов сил
- •2.8 Определение величины уравновешивающей силы методом н.Е. Жуковского
- •2.9 Расчет величины уравновешивающего момента и потребной мощности двигателя в исследуемом положении механизма
- •3 Контрольная работа для студентов механических специальностей
- •3.1 Структурный и кинематический анализ и синтез механизмов
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Указания к выполнению контрольной работы
- •3.2 Контрольная работа для студентов технологических специальностей
- •Задача 1
- •Задача 2
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •4 Экзаменационные задачи
- •Кинематический анализ рычажных механизмов
- •Планетарные механизмы
- •5 Курсовое проектирование. Общие указания
- •5.1 Цели курсового проектирования
- •5.2 Объём и содержание курсового проекта
- •5.3 Оформление чертежей
- •5.4 Оформление расчётно-пояснительной записки
- •6 Содержание проекта
- •6.1 Кинематический анализ механизма
- •6.2 Силовой анализ механизма
- •6.3 Синтез и анализ кулачкового механизма
- •6.4 Синтез и анализ зубчатого механизма
- •7 Пояснения и методические указания к выполнению проекта
- •7.1 Кинематический анализ механизма
- •7.2 Силовой анализ механизма
- •8 Синтез и анализ кулачкового механизма
- •Определение основных размеров кулачкового механизма.
- •Синтез и анализ зубчатого механизма
- •Графический метод (рисунок14)
- •Синтез зубчатого зацепления (рисунок 15).
- •9Специальные таблицы
- •10 Приложения
- •10.1 Задания по тематике общего машиностроения
- •Список контрольных вопросов
- •Литература
- •Министерство образования республики беларусь
2.6 Определение сил, приложенных к звеньям механизма
По условию задания
учитывается масса звеньев, совершающих
плоскопараллельное движение. Для этого
задается величина погонной массы q
(кг/м). Зная
длину звена l,
можно рассчитать его массу по формуле
![]() .
Массами звеньев 1, 3, 5 пренебрегаем. К
ползуну противоположно направлению
его движения прикладывается сила
сопротивления движению
.
Массами звеньев 1, 3, 5 пренебрегаем. К
ползуну противоположно направлению
его движения прикладывается сила
сопротивления движению
![]() .
В рассматриваемом примереFсопр=190
Н, q
= 40 кг/м. К точке
А
кривошипа прикладывается искомая
уравновешивающая сила
.
В рассматриваемом примереFсопр=190
Н, q
= 40 кг/м. К точке
А
кривошипа прикладывается искомая
уравновешивающая сила
![]() .
.
Определяем массы
звеньев:
![]()
![]()
Определяем силы
тяжести:
![]()
![]()
Модуль главного вектора сил инерции звена 2 найдем по формуле:
![]()
где
![]() –
ускорение центра масс звена 2,
–
ускорение центра масс звена 2,![]() .
Определяется оно при помощи плана
ускорений.
.
Определяется оно при помощи плана
ускорений.
![]()
![]()
Аналогично:
![]()
где
![]()
![]()
Главный момент сил инерции звена 2 определим по формуле:
![]() ,
,
где
![]() - момент инерции массы звена 2 относительно
его центра тяжести, кг×м2;
- момент инерции массы звена 2 относительно
его центра тяжести, кг×м2;
![]() ;
;
![]() -
угловое ускорение звена 2,
-
угловое ускорение звена 2,
![]() ;
определяется при помощи плана ускорений;
;
определяется при помощи плана ускорений;
![]() рад/с2
.
рад/с2
.
![]() =0,0033∙22,5=0,075
Н∙м
=0,0033∙22,5=0,075
Н∙м
Главный момент
сил инерции звена 4:
![]() кг∙м2
,
кг∙м2
,
где
![]() рад/с2
;
рад/с2
;
![]() =0,143∙24,11=3,45
Н∙м .
=0,143∙24,11=3,45
Н∙м .
Напоминаем, что направления сил инерции и моментов сил инерции противоположны соответствующим линейным и угловым ускорениям.
2.7 Расчет реакций в кинематических парах и величины уравновешивающей силы методом планов сил
Нахождение величин сил реакций начинаем с наиболее удаленной от кривошипа группы Ассура из звеньев 4 и 5. Вычерчиваем ее в произвольном масштабе и к соответствующим точкам прикладываем все активные силы, реакции связей, силы инерции и указываем направления действия моментов сил инерции (рисунок 2.10).
Так как группа Ассура была изображена в произвольном масштабе, то главный момент сил инерции приводим в соответствие с этим масштабом. Величину приведенного главного момента сил инерции определяем по формуле:
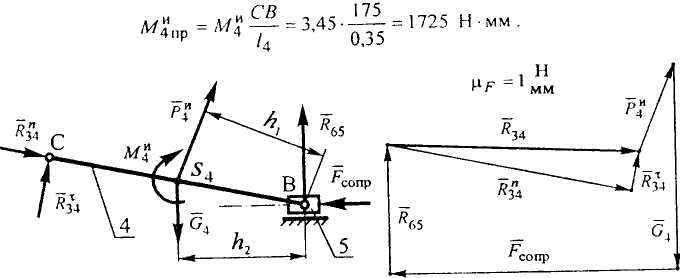
Рисунок 2.10 - Построение плана сил для группы Ассура из звеньев 4 и 5
В соответствии с принципом Даламбера должно выполняться следующее векторное уравнение:
![]() .
.
Величину касательной
составляющей реакции
![]() определяем из суммы моментов всех сил
относительно точкиВ:
определяем из суммы моментов всех сил
относительно точкиВ:
![]() ;
;
![]() ;
;
![]() H.
H.
Длину каждого
плеча
![]() измеряем
линейкой непосредственно на чертеже.
измеряем
линейкой непосредственно на чертеже.
Реакции
![]() и
и
![]() определяем при помощи плана сил (см.
рисунок 2.10). Построения начинаем с
известной составляющей реакции
определяем при помощи плана сил (см.
рисунок 2.10). Построения начинаем с
известной составляющей реакции![]() .
Это – сила
.
Это – сила![]() .
Затем
последовательно изображаем векторы
.
Затем
последовательно изображаем векторы
![]() .
Из конца вектора
.
Из конца вектора![]() проводим линию, параллельную
проводим линию, параллельную![]() ,
а из начала
,
а из начала![]() - параллельную
- параллельную
![]() .
Точка пересечения этих линий позволяет
определить положения и величины векторов
сил реакций
.
Точка пересечения этих линий позволяет
определить положения и величины векторов
сил реакций
![]() и
и
![]() .
.
Масштаб плана сил:
![]() .
Измеряя линейкой соответствующие
векторы и используя соотношение
.
Измеряя линейкой соответствующие
векторы и используя соотношение![]() (
(![]() -
длина вектора на плане сил в миллиметрах),
получаем следующие значения искомых
реакций:
-
длина вектора на плане сил в миллиметрах),
получаем следующие значения искомых
реакций:
![]()
![]()
![]()
Рассмотрим равновесие группы Ассура, образованной звеньями 2 и 3. В произвольном масштабе вычерчиваем группу Ассура и прикладываем к ней все активные силы, реакции, инерционные нагрузки (рисунок 2.11). Составляем уравнение равновесия:
![]() .
.
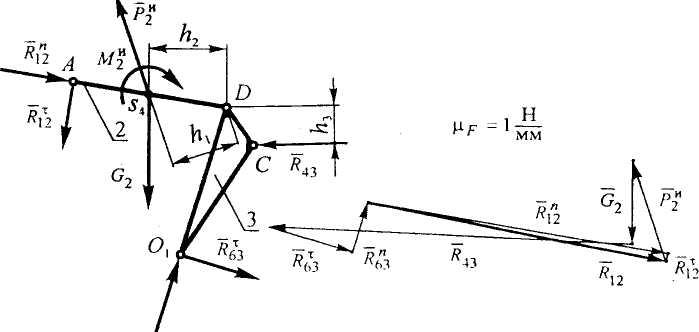
Рисунок 2.11 - Построение плана сил для группы Асура из звеньев 2 и 3.
Исходя из того,
что после приложения инерционных
нагрузок звено 2 считается находящимся
в состоянии равновесия, касательную
составляющую реакции
![]() можно определить из следующего уравнения:
можно определить из следующего уравнения:
![]()
![]()
где
![]() .
.
Решая уравнение, получим:
![]() H.
H.
Касательную
составляющую реакции
![]() определим из аналогичного уравнения
равновесия для звена 3:
определим из аналогичного уравнения
равновесия для звена 3:
![]() ;
;
![]()
![]()
Для
группы Ассура, образованной звеньями
2 и 3, строим план сил в масштабе
![]() .
Из плана сил определяем величину реакции
.
Из плана сил определяем величину реакции
![]()
![]()
Величину
уравновешивающей силы найдем, рассматривая
равновесие ведущего
звена (кривошипа). Для этого в произвольном
масштабе изображаем
ведущее звено и прикладываем в точке А
силу
Fyp
и
реакцию
![]() .
В соответствии с принципом Даламбера
имеем:
.
В соответствии с принципом Даламбера
имеем:
![]()
![]()
![]()
