Излучательная способность чёрного тела по Планку.
Как было показано нами ранее, излучательная способность абсолютно чёрного |
|||||||||||||
тела связана со спектральной плотностью излучения формулой |
|||||||||||||
|
|
r( ,T ) w c . |
|||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
w |
h 3 |
|
1 |
. |
|
|
|
||||
|
|
2c3 |
|
|
|
|
|
|
|||||
|
|
|
|
h |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e kT |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r( ,T ) |
h 3 |
|
|
1 |
. |
|
||||||
|
4 2c2 |
|
|
||||||||||
|
|
|
|
h |
|
||||||||
|
|
|
|
|
|
|
|
|
ekT 1 |
|
|||
Две последние формулы для спектральной плотности излучения и излучательной способности абсолютно чёрного тела называются формулами Планка.
Отметим, что при |
h |
1 |
формула Планка переходит в формулу Рэлея-Джинса. |
|
kT |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
h |
|
|
h |
1 следовательно, |
|
|
|
e |
kT |
1 |
kT , |
|
|
|||||
kT |
|
|
|
|
|
|
|||||||||
|
|
h 3 |
1 |
|
|
|
|
h 3 |
kT 2kT |
||||||
r( ,T ) |
|
|
|
|
|
|
|
|
h |
|
. |
||||
4 2c2 |
|
1 |
h |
1 |
|
4 2c2 |
4 2c2 |
||||||||
|
|
kT |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для того, чтобы сравнить результаты Планка с экспериментальными данными Вина, выразим излучательную способность через длину волны.
2 c , |
r( ,T ) |
h 3 |
|
|
1 |
|
|
h 8 3c3 |
|
1 |
. |
|||||||||||||
|
2 h |
|
|
|
|
|||||||||||||||||||
|
|
|
4 |
2 |
|
|
|
|
4 |
2 |
2 |
|
3 |
|
|
h 2 c |
|
|
||||||
|
|
|
|
c |
|
|
e kT |
1 |
|
|
|
c |
|
|
e |
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
kT |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
r( ,T ) 2 ch |
1 |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
3 |
2 ch |
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
e kT |
|
|
|
|
|
|
|
|
|
|
|||||
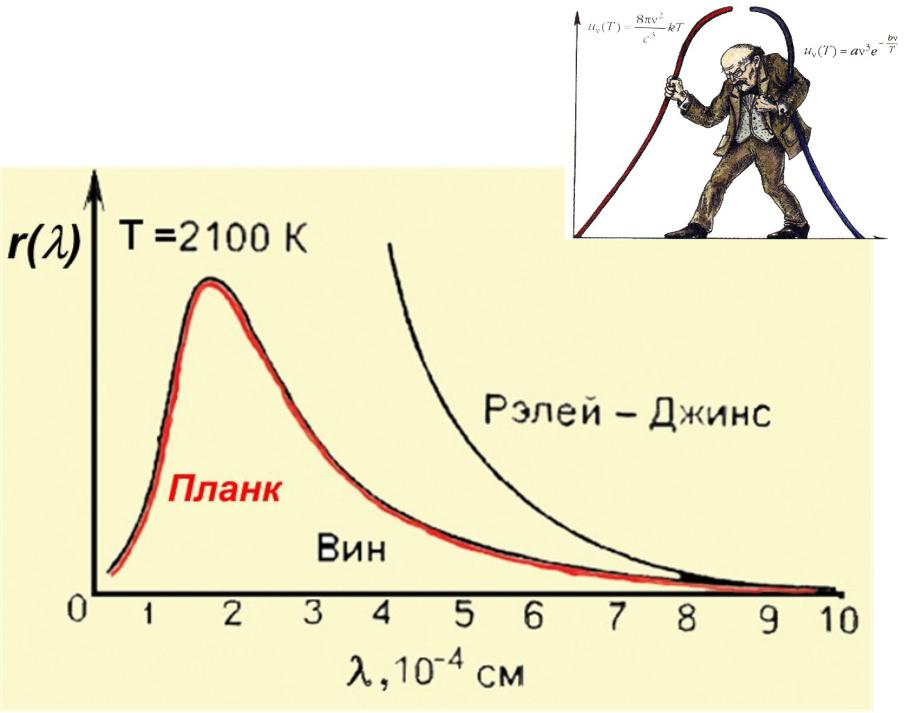
Излучательная способность чёрного тела по Планку.
Сравнение с экспериментом.
Интегральная энергетическая светимость чёрного тела по Планку.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегральная энергетическая светимость чёрного тела |
R(T ) r( ,T )d . |
|||||||||||||||||||||||||||||||||||||||
Подставим в этот интеграл формулу Планка. |
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h 3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
R(T ) |
|
|
|
|
|
|
|
|
d . |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 2c2 |
|
|
|
h |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
e kT 1 |
|
|
|
|
|
|
|
|
|||||
Обозначим |
|
|
x. |
|
Тогда |
kTx , |
|
d kT dx. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
h |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
3 |
3 |
x |
3 |
|
|
|
1 |
|
|
|
kT |
|
|
|
|
|
|
h |
|
kT |
4 |
|
x3 |
|||||||
|
R(T ) |
hk T |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|||||||||||
|
|
|
|
|
2 |
2 3 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
4 |
|
|
|
1 |
|
h |
|
|
4 |
2 |
c |
2 |
0 e |
x |
|
||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
c |
h e |
|
|
|
|
|
|
|
|
|
|
h |
|
|
1 |
||||||||||||||||
|
|
k4 |
|
|
|
|
|
|
x3 |
|
|
|
|
|
4 |
|
|
|
T |
4 |
. |
|
Этот |
|
результат |
|
полностью |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
2 |
3 |
0 e |
x |
|
|
dx |
|
T |
|
|
|
|
|
согласуется с законом Стефана |
||||||||||||||||||||||
|
4 |
|
c |
|
h |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
– Больцмана. |
|
|
|
|
|
|
||||||||||||||
Вычисление коэффициента σ даёт
|
|
k |
4 |
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
dx |
5,6696 10 8 |
(Вт/(м2·К4). |
||
|
|
|
|
|
|
|
|||||
|
|
|
2h3 |
0 ex 1 |
|
|
|||||
|
4 2c |
|
|
||||||||
На самом деле, Планк получил значение постоянной h из условия равенства этого выражения экспериментальному значению постоянной Стефана – Больцмана.
Выводы.
Объяснить закономерности теплового излучения можно лишь использовав два предположения:
-электромагнитные волны испускаются порциями – квантами, причём энергия одного кванта равна E = hν;
-при подсчёте плотности энергии излучения следует отказаться от закона равного распределения энергии по степеням свободы в пользу применения распределения Больцмана.
Остальные исходные предположения теории равновесного теплового излучения (модель абсолютно чёрного тела, модель равновесного теплового излучения) одинаковы как в классической теории Рэлея и Джинса, так и в квантовой теории излучения Планка.
