
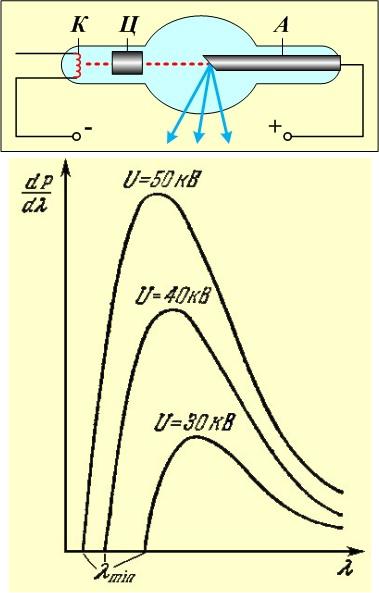
- •5.8. Электроны
- •Катодные лучи
- •Катодные лучи
- •Гипотезы:
- •Катодные лучи
- •Открытие электрона
- •Открытие электрона
- •Кавендишская лаборатория
- •5.9. ФОТОНЫ
- •Открытие фотоэффекта Герцем
- •Исследования А. Г. Столетова
- •Исследования Леннарда и Томсона
- •Законы фотоэффекта
- •Почему нельзя объяснить фотоэффект с классических позиций?
- •Уравнение Эйнштейна для фотоэффекта
- •Свойства фотонов
- •5.10.ФОТОНЫ
- •Другие доказательства существования фотонов. Опыт Ботэ.
- •5.11. ФОТОНЫ
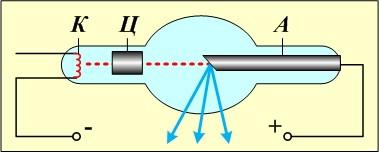
- •Рентгеновское излучение (X-лучи)
- •Тормозное и характеристическое рентгеновское излучение
- •Коротковолновая граница спектра тормозного рентгеновского излучения.
- •5.12.ФОТОНЫ
- •Эффект Комптона.
- •Экспериментально было установлено, что изменение длины волны при рассеянии рентгеновского излучения составляет
- •До столкновения. После столкновения.
- •Второе уравнение системы – векторное. Для его решения применим теорему
- •5.13. ФОТОНЫ
- •Давление света.
- •Найдём импульс, передаваемый поверхности тела n поглощаемыми фотонами.
- •2. Фотоны полностью отражаются.
- •3. Пусть на поверхность падают N фотонов, из них N1 поглощаются, а N2
- •Корпускулярно-волновой дуализм света
Тормозное и характеристическое рентгеновское излучение
Тормозное излучение возникает при движении заряженных частиц с ускорением (например, при торможении ранее ускоренных электронов). Спектр тормозного излучение – непрерывный.
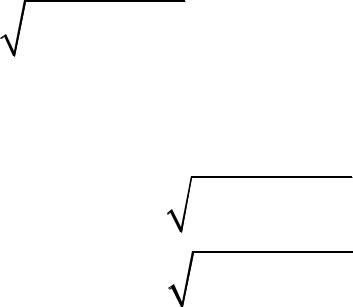
Для тормозного излучения наблюдается некоторая граничная частота (или наименьшая длина волны), выше которой электромагнитные волны не излучаются. Величина наименьшей длины волны (наибольшей частоты) зависит от величины ускоряющего напряжения (см. рис.)
Кроме тормозного излучения наблюдается
характеристическое излучение, специфи- ческое для каждого вещества. Спектр характеристического излучения – дискретный.
Коротковолновая граница спектра тормозного рентгеновского излучения.
Существование коротковолновой границы тормозного рентгеновского излучения легко объяснить, исходя из квантовой природы излучения.
Величина энергии, излучаемой электроном при торможении, не может превысить величины энергии, полученной электроном при ускорении.
|
|
h eU. |
|
|
2 c |
, |
|
|
|||
|
2 hc |
|
|
|
2 hc |
|
|
hc |
|
||
h |
eU , |
min |
, |
min |
, |
||||||
eU |
|||||||||||
|
|
|
eU |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
что совпадает с экспериментально полученной величиной |
|
|
|||||||||
min |
12390 , |
где длина волны выражена в ангстремах, напряжение |
|||||||||
|
|
U |
|
– в вольтах. |
|
|
|
|
|
||

5.12.ФОТОНЫ
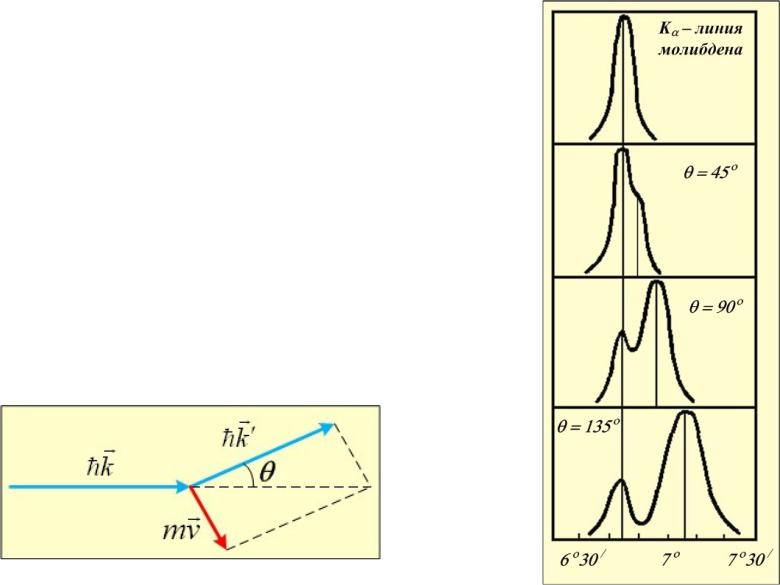
Эффект Комптона.

Эффект Комптона.
(Неупругое рассеяние рентгеновских фотонов на электронах)
Э. Комптон в 1922 – 23 г. исследовал взаимодействие характеристического рент- геновского излучения мо- либдена (K – линию) с
различными веществами.
Он обнаружил, что если наблюдать спектр излу- чения молибдена под неко- торым углом к оси исход- ного рентеновского пучка, то появляется дополнитель- ная длинноволновая линия.
Интенсивность и длина волны этой длинноволновой линии
– спутника (или сателлита) зависит только от угла наблюдения и не зависит от рода облучаемого вещества.
Экспериментально было установлено, что изменение длины волны при рассеянии рентгеновского излучения составляет
1 cos 2 sin2 ,2,42 10 12 (м).
Объяснить этот эффект можно, рассмотрев взаимодействие рентгеновских фотонов с электронами. (Если бы фотоны взаимодействовали с атомами вещества, результат зависел бы от рода вещества).
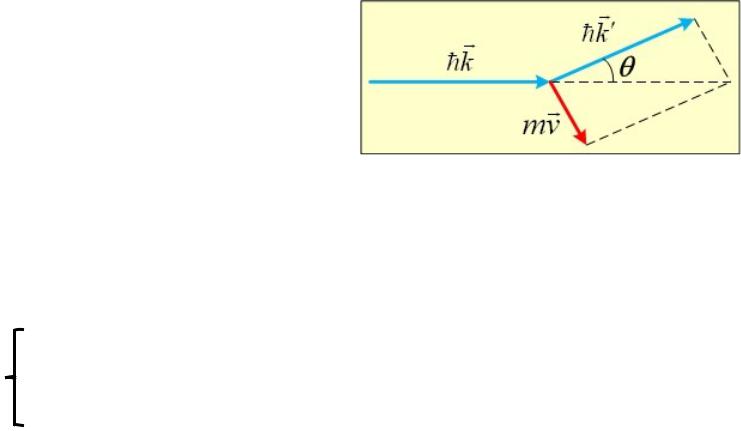
Рассмотрим столкновение рентгеновского фотона с электроном.
mv
импульс электрона, угол рассеяния,
hk hk
импульс фотона до столкновения, импульс фотона после столкновения.
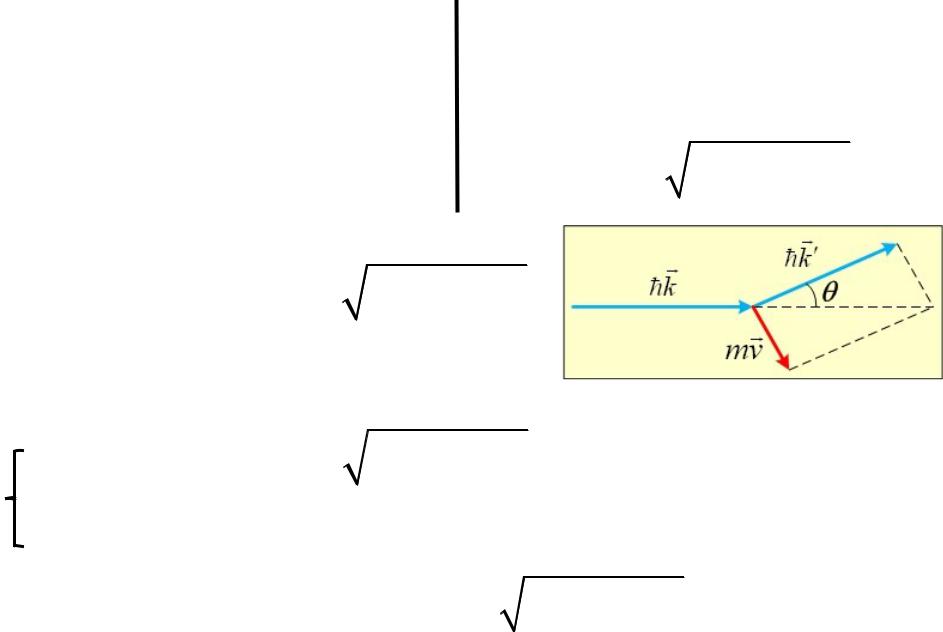
До столкновения. После столкновения.
Фотон: |
p hk , |
E h . |
Фотон: |
p hk , E h . |
|
|
|
|
|
||
Электрон: p 0, |
E mc2. |
Электрон: p 0, |
|
||
|
|
|
E c p2 m2c2 . |
|
|
Закон сохранения энергии:
h mc2 h c p2 m2c2 .
Закон сохранения импульса:
hk hk p.
h mc2 h c p2 m2c2 , hk hk p.
h |
mc h |
p2 |
c |
c |
|
Разделим первое уравнение системы на скорость света c:
m2c2 ,
|
mc |
|
|
|
|
|
p |
2 |
m |
2 |
c |
2 |
, |
|
|
|
|
k, |
|
|
|
||||||||||||
h c |
|
h c |
|
|
|
|
|
|
|
|
|
c |
c |
|
k , |
||||||||||||||||||
|
k,k |
модули волновых векторов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
hk mc hk |
|
p2 m2c2 , |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
h k k mc |
|
p |
|
|
|
c |
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
||||||||||||||||||||
Возведём в квадрат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
h k k mc |
|
|
|
p |
|
m |
c |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
c |
2 |
p |
2 |
2 |
|
2 |
. |
|||||
|
|
h |
k |
|
|
|
2h k k mc m |
|
|
m |
c |
||||||||||||||||||||||
|
|
|
|
p2 h2 |
k k 2 2hmc k k . |
|
|
|
|
||||||||||||||||||||||||
Второе уравнение системы – векторное. Для его решения применим теорему
косинусов. |
hk hk |
p, |
|
|||||||
|
|
r |
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
||
h k k |
|
p, |
|
|||||||
|
2 |
|
||||||||
|
r |
|
r |
|
|
|
|
|||
Возведём в квадрат: |
|
|
|
|
pr2 , |
|
||||
h2 |
k k |
|
|
|||||||
|
|
|
p2 |
h2 |
k2 |
2kk cos k 2 . |
||||
|
|
p2 |
h2 k k 2 2hmc k k . |
|||||||
|
|
p2 |
h2 |
k2 |
2kk cos k 2 , |
|||||
Первое уравнение получено из закона сохранения энергии, второе уравнение системы – из закона сохранения импульса.
h2 k2 2kk cos k 2 h2 k k 2 2hmc k k .
h2 k2 2kk cos k 2 h2 |
k k |
2 2hmc k k , |
|||||||||||||||||
h2k2 2h2kk cos h2k 2 h2k2 2h2kk h2k 2 |
2hmc k k , |
||||||||||||||||||
hkk cos hkk mc k k , |
|
|
|||||||||||||||||
|
hkk hkk cos mc k k , |
|
|
||||||||||||||||
|
hkk |
1 cos mc |
k k |
, |
|
|
: mc kk |
||||||||||||
|
|
||||||||||||||||||
|
kk |
|
|
|
|
|
mc |
|
k k |
|
|
|
|
||||||
|
h |
|
|
1 cos |
|
|
|
|
|
, |
|
|
|||||||
|
mckk |
|
|
|
mckk |
|
|
|
|||||||||||
|
|
|
h |
1 cos |
|
k k |
|
, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
mc |
|
kk |
|
|
|
|
|
||||||||||
|
|
|
|
h |
|
|
1 |
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
1 cos |
|
k |
, |
|
|
|
|
||||||||
|
|
|
mc |
k |
|
|
|
|
|||||||||||

|
h |
|
|
1 |
|
1 |
|
|
|
|
1 cos |
|
k , |
|
|||
|
mc |
k |
|
|||||
2 h |
1 cos |
2 |
|
2 |
, |
|||
mc |
k |
k |
||||||
2mch 1 cos ,
|
|
|
2 h |
|
|
|
h |
|
||
|
|
|
|
|
|
|
|
|
|
|
mc |
|
1 cos mc 1 cos . |
||||||||
|
|
|||||||||
|
|
2 h |
|
h |
2,42 10 12 |
(м). |
||||
|
mc |
|||||||||
|
|
|
mc |
|
|
|
|
|
|
|
