4.5. Дифракция Фраунгофера на периодической структуре.
|
|
|
N |
|
|
|
|
Итак, |
SN e 2 |
n 1 . |
|
|
|
||
N |
|
|
n 1 |
|
|
|
|
|
2 |
n 1 |
e 2i e 4i e 6i ... e |
2 |
|
N 1 |
|
SN e |
|
1 |
|
|
|||
n 1
Как видно из формулы, S – частичная сумма геометрической прогрессии. Знаменатель этой прогрессии
q e 2i .
Частичная сумма геометрической прогрессии со знаменателем q вычисляется по формуле
SN 11 qqN .
4.5. Дифракция Фраунгофера на периодической структуре.
SN |
1 qN |
, |
q e 2i . |
SN |
1 e 2i N . |
|
|
1 q |
|||||
|
|
|
|
|
1 e 2i |
|
Уравнение волны, излучаемой всеми точечными источниками всех щелей.
|
sin u |
|
|
b |
sin |
|
N |
|
k n 1 d sin |
|
||||
|
|
|
|
|
|
|
|
|||||||
E E0 |
|
e |
i t k |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||||
u |
|
|
|
|
e |
|
|
|
|
|||||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|||
E sin u |
1 e |
2i N |
|
|
|
k |
b |
sin |
|
|
||||
|
i t |
2 |
. |
|
||||||||||
|
|
|
e |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 u |
|
1 e 2i |
|
|
|
|
|
|
|
|
||||
Интенсивность излучения, испущенного из всей решётки в
рассматриваемом направлении определяется квадратом амплитуды
I : E 2 .
4.5. Дифракция Фраунгофера на периодической структуре.
I :
I
|
|
|
|
|
|
|
sin u |
|
1 e |
2i N |
|
|
|
|
|
b |
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
i t k |
2 |
sin |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
E |
. |
E E0 |
u 1 e 2i e |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
. |
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
2 |
|
1 e |
2i N |
|
2 |
|
|
|
|
b |
sin |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
E2 sin u |
|
|
|
i t k |
2 |
|
|
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
e |
|
|
|
|
|
||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
1 |
e |
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
sin u |
2 |
|
1 e 2i N |
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
I0 |
u |
|
|
1 |
e |
2i |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вычислим квадрат модуля комплексного числа, входящего в эту формулу.
4.5. Дифракция Фраунгофера на периодической структуре.
Вычислим квадрат модуля комплексного числа, входящего в эту формулу.
1 e 2i N |
|
2 |
|
1 e 2i N 1 e2i N |
|
1 e 2i N e2i N 1 |
. |
||||||||||||
|
|||||||||||||||||||
1 e 2i |
|
|
|
|
|
1 e 2i e2i 1 |
|||||||||||||
|
|
1 e 2i 1 e2i |
|
|
|||||||||||||||
Числитель: |
|
|
|
|
|
e 2i N e2i N |
|
|
|
|
|||||||||
1 e 2i N e2i N 1 2 2 |
|
|
|
||||||||||||||||
2 1 cos 2N |
2 2sin |
2 |
|
2N |
|
|
|
2 |
N . |
|
|||||||||
|
|
|
|
2 |
|
4sin |
|
|
|
||||||||||
Знаменатель: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
e 2i |
|
e2i |
|
|
|
|
|
|||||||
1 e 2i e2i |
1 2 2 |
|
|
|
|
|
|
||||||||||||
2 1 cos 2 |
2 2sin |
2 2 |
|
|
4sin |
2 |
|
. |
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.5. Дифракция Фраунгофера на периодической структуре.
|
|
|
1 e 2i N |
|
2 |
|
4sin2 |
N |
|
|
sin2 N |
. |
||||
|
|
|
|
|||||||||||||
|
|
|
1 e 2i |
|
|
4sin2 |
|
|
sin2 |
|||||||
Итого |
|
|
|
|
|
sin2 u |
sin2 |
N |
|
|
|
|||||
|
|
|
|
I |
I0 |
u2 |
sin2 |
|
|
, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
d sin , |
u b sin . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
sin2 u |
|
характеризует распределение интенсивности излучения |
||||||||||||||
u2 |
|
|||||||||||||||
|
в результате дифракции на одной щели. |
|
||||||||||||||
sin2 |
|
N |
|
характеризует распределение интенсивности излучения |
||||||||||||
|
|
в результате интерференции пучков, исходящих из |
||||||||||||||
sin2 |
|
|||||||||||||||
|
различных щелей. |
|
|
|
|
|
|
|
||||||||
4.5. Дифракция Фраунгофера на периодической структуре.
I |
|
sin2 u |
|
||
1 |
|
u2 |
|
|
Поведение этой функции было исследовано при рассмотрении вопроса о дифракции на отверстии.
Она имеет максимумы при
b sin 2m 1 2 ,
и минимумы при
b sin m .
График этой функции показан на рисунке.
4.5. Дифракция Фраунгофера на периодической структуре.
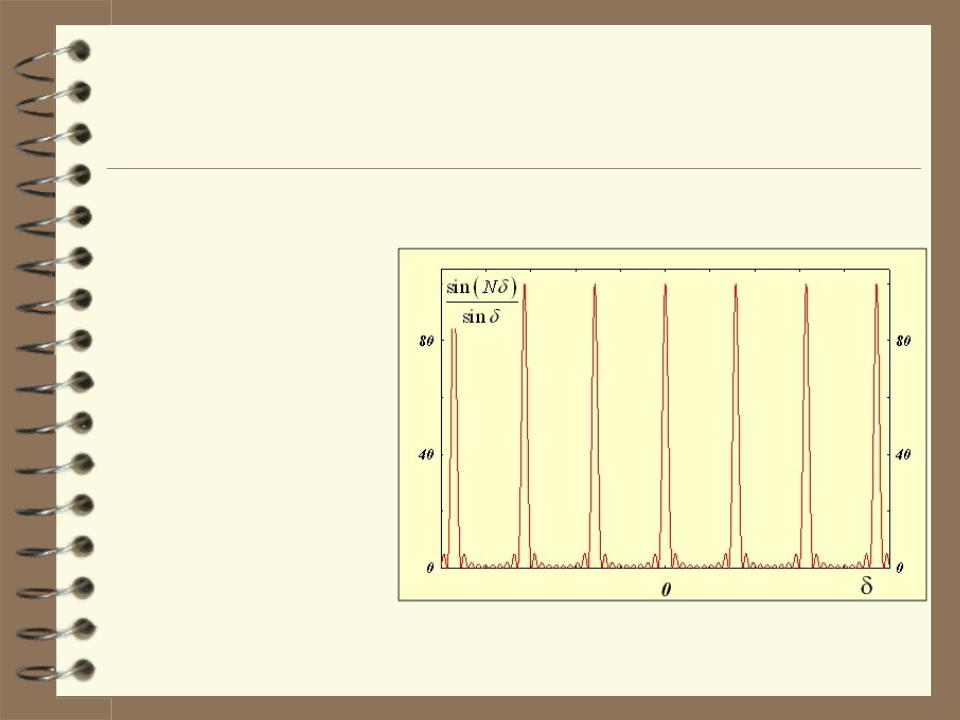
Рассмотрим поведение функции, описывающей результаты интерференции пучков, исходящих из различных отверстий,
|
|
|
N |
2 |
||
|
|
|
||||
I2 |
|
sin |
. |
|||
|
|
|
||||
|
|
|
|
|
|
|
|
|
sin |
|
|||
Известно, что |
|
|
|
|||
lim |
sin N |
|
N. |
|||
sin |
|
|||||
0 |
|
|
|
|
||
Эти |
|
значения |
являются |
|||
максимумами функции. |
||||||
При |
0 |
|
|
|||
I2 N 2 , |
где N – число щелей дифракционной решётки |
|||||
|
|
|
|
|
(обычно оно очень велико). |
|
4.5. Дифракция Фраунгофера на периодической структуре.
Максимумы функции наблюдаются при
0.
d sin m ,
m – целое.
d sin m ,
d sin m .
Максимумы интенсивности излучения, возникающие при выполнении последнего условия называются главными максимумами.
Остальные максимумы интенсивности излучения (см. график) называются побочными максимумами.
4.5. Дифракция Фраунгофера на периодической структуре.
Побочные максимумы возникают, когда
sin N 0,
но, в то же время
sin 0.
Перечислим условия наблюдения всех максимумов. Условия наблюдения главных максимумов выделены красным.
Nδ = 0, π, 2π, …, (N-1)π, Nπ, (N+1)π, …, (2N-1)π, 2Nπ, (2N+1)π, … .
4.5. Дифракция Фраунгофера на периодической структуре.
Результирующая интенсивность является произведением двух
функций: |
|
|
|
sin2 u |
sin2 |
N |
|
|
|
I |
I0 |
u2 |
sin2 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
где |
d sin , |
u b sin . |
||||||
|
|
|
|
|
|
|
|
|
На следующем рисунке этот факт проиллюстрирован для соотношения между шириной щели и периодом дифракционной решётки
db 4.