А5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0,1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию Ek брошенного камня через время t = 0,5 с после начала его
движения.
Дано: m = 2 кг
= 0,1 м/с
M = 100 кг t = 0,5 с
Ek = ?
Решение
Скорость, которую приобретёт тележка с человеком, найдём из закона сохранения импульса. Запишем закон сохранения импульса в лабораторной системе
отсчёта.
0 Mv mu.
В проекции на ось OX (см. рисунок)
0 Mv mu.
Отсюда величина скорости камня после броска
u Mvm .
А5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0,1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию Ek брошенного камня через время t = 0,5 с после начала его
движения.
Решение (продолжение)
После броска камень движется в однородном поле силы тяжести. Его движение вдоль оси OX равномерное, вдоль оси – равноускоренное с ускорением, равным g и направленным вниз.
Через t = 0,5 с после броска скорость камня имеет две компоненты:
u1 u1x i u1y j, |
|
|||||||
|
u2 |
u2 |
u2 . |
|
|
|
||
|
|
1 |
|
1x |
1y |
|
|
|
Кинетическая энергия камня: |
|
mu2 |
|
mu2 |
|
mu12y |
. |
|
Ek |
|
|
1 |
|
1x |
|
|
|
|
2 |
|||||||
|
|
|
2 |
|
2 |
|
|
|
Движение камня вдоль оси OX равномерное, поэтому
u1x u1 const.
А5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0,1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию Ek брошенного камня через время t = 0,5 с после начала его
движения.
Решение (продолжение)
Вдоль оси OY движение равноускоренное с |
|
|
|||||||
ускорением, равным g и направленным вниз |
|
|
|||||||
поэтому |
|
|
|
|
|
|
|
|
|
u1y gt. |
|
|
|
|
|
||||
Ek mu12 |
mu12x |
mu12y |
m M 2v2 |
||||||
|
|||||||||
2 |
2 |
|
2 |
|
|
2 |
|
m2 |
|
|
|
|
M 2v2 |
|
mg |
2t2 |
|||
|
|
2m |
2 |
. |
|||||
|
|
|
|
|
|
||||
mg2t2
2
|
2 |
2 |
2 |
2 |
100 |
2 |
0,1 |
2 |
|
2 9,8 |
2 |
0,5 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
EДжM v |
|
mg t |
|
|
|
|
|
|
|
|
|
|
|
»49 |
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
k |
2m |
|
2 |
|
|
|
2 2 |
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: Ek = 49 Дж.
А8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h0 = 0,5 м, если акробат прыгает в нее с высоты H0 = 1 м.
Дано: Н = 8 м
h0 = 0,5 м H0 = 1 м h - ?
Решение
Если пренебречь силой сопротивления воздуха, то на акробата действуют силы тяжести и упругости. Обе эти силы консервативны. Поэтому изменение полной механической энергии равно нулю.
E E U |
U |
0. |
kтяж |
упр |
|
В начале и в конце прыжка скорость акробата рано нулю, поэтому изменение кинетической энергии равно нулю.
Ek 0.
Uтяж mgy1 mgy0 mg H h .
Потенциальная энергия акробата в поле силы тяжести уменьшилась.
Для прыжка высоты H0:
Uтяж mgy1 mgy0 mg H0 h0 .
А8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h0 = 0,5 м, если акробат прыгает в нее с высоты H0 = 1 м.
Решение (продолжение)
Изменение потенциальной энергии упругой сетки можно
определить как 2 2
U упр kx22 kx21 ,
где x – абсолютная деформация сетки, k – её коэффициент жёсткости. Для прыжков с разных высот
H : |
x2 h, |
|
|
x1 0; |
|
H0 : |
x2 h0 , |
|
x1 0. |
||
Для прыжка высоты H: |
kh2 |
|
|||
|
U упр |
|
, |
||
|
|
|
2 |
||
Для прыжка высоты H0: |
|
|
|||
kh2 |
|
||||
|
U упр |
|
|||
|
|
0 . |
|||
|
|
|
|
2 |
|
Потенциальная энергия деформированной сетки возрастает в обоих случаях.
А8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h0 = 0,5 м, если акробат прыгает в нее с высоты H0 = 1 м.
Решение (продолжение)
Изменение механической энергии для прыжка высоты H:
Uтяж U упр mg H h kh22 0.
Для прыжка высоты H0:
Uтяж U упр mg H0 h0 kh202 0.
Таким образом, получаем два уравнения:
kh22 mg H h , kh202 mg H0 h0 .
Разделив первое уравнение на второе, получим:
h2 |
|
H h |
. |
|||
h2 |
H |
0 |
h |
|||
|
|
|||||
0 |
|
|
0 |
|
||
А8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h0 = 0,5 м, если акробат прыгает в нее с высоты H0 = 1 м.
Решение (продолжение)
|
|
h2 |
|
H h |
. |
|
|||
|
|
h2 |
H |
0 |
h |
|
|||
|
|
|
|
|
|||||
|
|
0 |
|
|
|
0 |
|
|
|
H0 h0 h2 h02h h02 H 0. |
|
||||||||
|
h2 |
h4 |
4 H |
0 |
h h2 H |
|
|||
h |
0 |
|
0 |
|
|
|
0 0 |
. |
|
|
|
2 H0 h0 |
|||||||
1,2 |
|
|
|
||||||
|
|
|
|
||||||
Высотв над землёй должна быть положительна, поэтому
|
h2 |
h4 |
4 H |
0 |
h h2 H |
1, 2 |
. |
hм |
0 |
0 |
|
0 0 |
|||
|
2 H0 h0 |
||||||
|
|
|
|
||||
Ответ: h = 1,2 м.
А10. Льдина площадью поперечного сечения S = 1 м2 и высотой h = 0,4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду?
Дано: S = 1 м2
h = 0,4 м
A = ?
Решение
Первоначально льдина плавает, то есть находится в положении равновесия.
Векторная сумма сил, приложенных к льдине, равна нулю.
r |
r |
0. |
mg |
FA0 |
Здесь FA0 – сила Архимеда, действующая на льдину в положении равновесия. Величина этой силы
FA0 0 gV0 ,
где 0 – плотность воды, V0 – объём части льдины, погружённой в воду.
По мере погружения льдины в воду объём погружённой части будет расти. Следовательно, будет расти и сила Архимеда, действующая на льдину.
Если мы хотим погружать льдину очень медленно (без возрастания её кинетической энергии), то мы должны прикладывать к ней такую внешнюю силу F, чтобы в каждый момент времени можно было считать, что льдина находится в равновесии.
А10. Льдина площадью поперечного сечения S = 1 м2 и высотой h = 0,4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду?
Решение (продолжение)
Пусть льдина погружена на некоторую глубину x. По сравнению с положением равновесия сила Архимеда
возросла. |
r |
r |
r |
|
|
|
|
|
|
|
|||
|
|
FA FA0 |
FA1 |
, |
|
|
|
|
FA0 0 gV1, |
|
|
||
V1 |
Sx - объём, ушедший |
под |
воду |
в процессе |
||
|
|
принудительного |
погружения |
льдины под |
||
действием силы F.
Векторная сумма сил, приложенных к льдине, равна нулю.
mg FA0 FA1 F 0.
В проекции на вертикальную ось, направленную вверх,
mg FA0 FA1 F 0.
Но, как было показано ранее, mg FA0 0, поэтому, F FA1.
А10. Льдина площадью поперечного сечения S = 1 м2 и высотой h = 0,4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду?
Решение (продолжение)
Таким образом, сила, которую следует прикладывать для очень медленного погружения льдины равна
FFA1 0 gV1 0 gSx.
Сростом глубины погружения величина прикладываемой силы должна возрастать.
Работу этой переменной силы вычислим по формуле |
||
s2 |
r r |
s2 |
A Fds |
F cos ds. |
|
s1 |
|
s1 |
Величина вектора перемещения в данном случае равна глубине погружения льдины:
s x.
Направление вектора перемещения в данном случае совпадает с направлением силы,
cos 1.
Пределы интегрирования: |
x1 0, |
x2 h h0. |
h0 глубина, на которую погружена плавающая льдина.
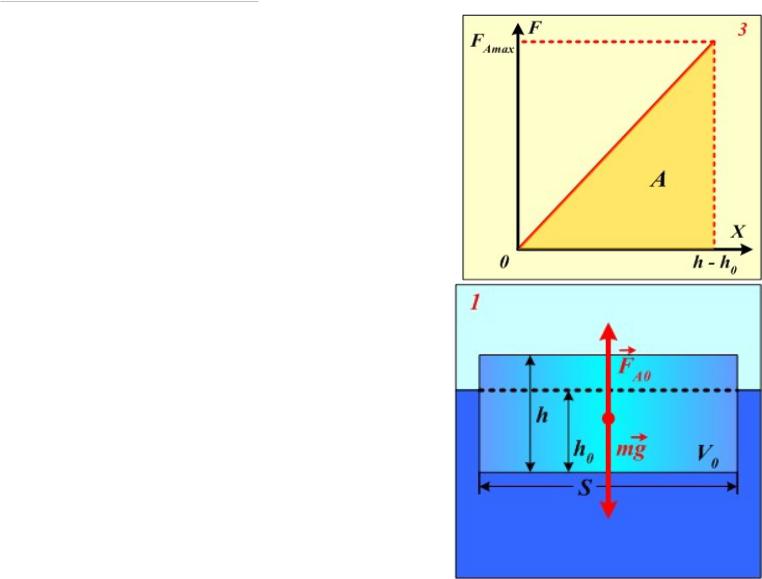
А10. Льдина площадью поперечного сечения S = 1 м2 и высотой h = 0,4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду?
Решение (продолжение)
Работа по погружению льдины
x |
|
|
|
|
h h |
h h |
|
|
|
||
A 2 |
F cos dx |
|
0 |
Fdx 0 |
0 gSxdx |
||||||
x1 |
|
|
|
h h0 |
0 |
|
|
0 |
|
|
|
|
|
0 gSx2 |
|
|
|
|
0 gS h h0 |
2 |
|||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
. |
||
|
2 |
|
0 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Графически работа численно равна площади треугольника на рисунке.
Чтобы определить величину h |
, вернёмся к рисунку 1. |
||
r |
0 |
r |
0. |
mg |
FA0 |
||
В проекции на вертикальную ось, направленную вверх,
|
mg FA0 0. |
|
FA0 0 gV0 , |
V0 Sh0 , |
mg gV gSh, |
- плотность льда.
А10. Льдина площадью поперечного сечения S = 1 м2 и высотой h = 0,4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду?
Решение (продолжение)
|
|
|
mg FA0 0. |
|
|
|
|
|||||||
FA0 0 gV0 , |
V0 Sh0 , |
mg gV gSh, |
||||||||||||
|
|
|
gSh 0Sh0 . |
|
|
|
|
|||||||
|
|
|
|
h h |
|
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Окончательно, работа по погружению льдины |
2 |
|
||||||||||||
|
|
|
2 |
|
|
|
gS |
h h |
|
|
|
|||
|
|
|
|
|
|
|||||||||
|
0 gS h h0 |
|
|
0 |
|
|
0 |
|||||||
A |
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
2 |
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
gSh2 |
0 |
2 |
7,84 |
. |
|
|
|||||||
AДж |
2 0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: А = 7,84 Дж.