
- •Работа. Энергия. Применение законов сохранения.
- •А1. Найти работу A, которую нужно совершить, чтобы увеличить скорость движения тела массой
- •А1. Найти работу A, которую нужно совершить, чтобы увеличить скорость движения тела массой
- •А2. Камень падает с некоторой высоты без начальной скорости в течение времени t
- •А2. Камень падает с некоторой высоты без начальной скорости в течение времени t
- •А6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и
- •А6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и
- •А6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и
- •А6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и
- •А6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и
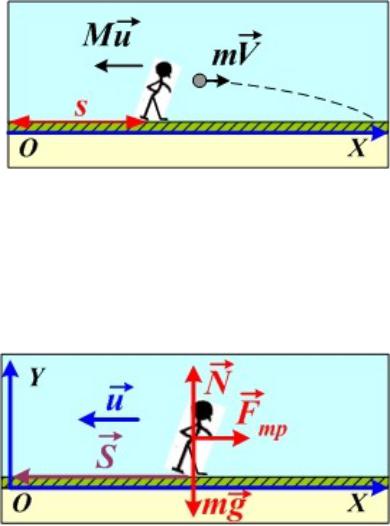
- •А5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m
- •А5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m
- •А5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m
Работа. Энергия. Применение законов сохранения.

А1. Найти работу A, которую нужно совершить, чтобы увеличить скорость движения тела массой m = 1 т от 1 = 2 м/с до 2 = 6 м/с на пути S = 10 м. На всем пути действует
сила трения Fтр = 2 Н.
Дано: |
|
|
|
Решение |
|||
|
|
|
|||||
m =1000 кг |
|
|
|
|
|
|
|
|
Согласно определению, работа |
||||||
u1 |
= 2 м/c |
|
|||||
|
s2 |
r r |
|
s2 |
|||
u2 |
= 2 м/c |
|
|
||||
F = 2 H |
|
A Fds |
F cos ds. |
||||
А = ? |
|
s1 |
|
|
s1 |
||
F – внешняя сила , s – перемещение, α – угол между векторами силы и перемещения.
Выберем направление оси OX так, чтобы оно совпадало с направлением скорости тела (см.рис.). Скорость возрастает, следовательно, ускорение направлено вправо, а силы – так как показано на рисунке. Запишем второй закон Ньютона в проекции на ось OX.
ma F Fтр .
Отсюда
F ma Fтр .
Величину ускорения найдем из кинематического уравнения:
a V22 V12 . 2S

А1. Найти работу A, которую нужно совершить, чтобы увеличить скорость движения тела массой m = 1 кг от 1 = 2 м/с до 2 = 6 м/с на пути S = 10 м. На всем пути
действует сила трения Fтр = 2 Н.
Решение (продолжение)
F ma Fтр . |
a |
V 2 |
V 2 |
2 |
1 . |
||
|
|
2S |
|
F m V222SV12 Fтр .
Сила, действующая на тело, постоянна. Угол между векторами силы и перемещения равен нулю, cos0 = 1.
|
s2 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
A |
|
F cos ds |
F |
S cos |
F |
S |
|
V1 |
F |
|
||||||
|
m V2 |
S |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2S |
|
тр |
|
|
|
|
s1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
V22 V12 |
Fтр S. |
|
36 4 |
2 10 |
|
36 |
|
. |
|
|
|||||
|
2 |
AДж |
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: A = 36 Дж

А2. Камень падает с некоторой высоты без начальной скорости в течение времени t = 1,43 с. Найти кинетическую энергию камня Ek и изменение его потенциальной энергии
U к тому моменту, когда камень достигнет средней точки пути. Масса камня m = 2 кг.
Дано: |
|
|
Решение |
|
|
|
1. Выберем начало отсчёта потенциальной |
||||
t = 1,43 c |
|
||||
m = 2 кг |
|
энергии в точке падения камня (см. |
|||
|
|
рисунок). |
|
|
|
Ek = ? |
|
2. Если пренебречь силой сопротивления |
|||
U = ? |
|
воздуха, то в системе действует только сила |
|||
|
|||||
|
|
тяжести, которая является потенциальной. |
|||
|
|
Следовательно, |
изменение |
полной |
|
|
|
механической энергии равно нулю (полная |
|||
|
|
механическая энергия сохраняется) |
|
||
E 0.
E Ek U 0.
U - потенциальная энергия тела в однородном поле силы тяжести.
U U1 U0 mg H2 mgH mg H2 .

А2. Камень падает с некоторой высоты без начальной скорости в течение времени t = 1,43 с. Найти кинетическую энергию камня Ek и изменение его потенциальной энергии
U к тому моменту, когда камень достигнет средней точки пути. Масса камня m = 2 кг.
Решение (продолжение)
Высоту, с которой падает тело найдём кинематического уравнения движения:
y(t) H |
gt2 |
0, |
H |
gt |
2 |
. |
|||
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
||
H |
mg2t2 |
|
2 9,82 |
1, 432 |
|
|
|
||
U mgДж |
|
|
|
|
|
98 |
|||
4 |
4 |
|
|||||||
2 |
|
|
|
|
|
|
|||
E Ek U 0.Ek U.
из
.
В верхней точке тело покоится, следовательно в этой точке Ek = 0. Поэтому
Ek Ek1 Ek 0 Ek1 UДж98 |
. |
Ответ: Ek = 98 Дж, ΔU = - 98 Дж.

А3. Тело массой m = 3кг, имея начальную скорость 0 = 0, скользит по наклонной
плоскости высотой h = 0,5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2,45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q, выделившееся при трении.
Дано: m = 3кг
0 = 0
h = 0,5 м l = 1 м
= 2,45 м/c
- ?
Q - ?
Решение
Если пренебречь силой сопротивления воздуха, то в системе действуют сила тяжести и сила упругости, которые являются консервативными и неконсервативная сила трения. Поэтому изменение полной энергии тела равно работе неконсервативной силы.
E E U A .
kтр
Тело движется в однородном поле силы тяжести, высота над землёй уменьшается,
поэтому
U mgh.
Скорость движения тела возрастает от нуля до v, поэтому
Ek mv2 2 mv202 mv2 2 .

А3. Тело массой m = 3кг, имея начальную скорость 0 = 0, скользит по наклонной
плоскости высотой h = 0,5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2,45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q, выделившееся при трении.
Решение (продолжение)
E U A .
kтр
Aтр Ek U mv2 2 mgh.
Если считать, что количество выделившейся теплоты равно работе силы трения, то
Q |
mv2 |
3 2, 452 |
3 9,8 0,5 |
5,7 |
. |
|
2 |
mghДж |
2 |
||||
|
|
|
|
|
||
Знак «-» указывает на то, что энергия в виде тепла выделилась, «ушла» из системы.

А3. Тело массой m = 3кг, имея начальную скорость 0 = 0, скользит по наклонной
плоскости высотой h = 0,5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2,45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q, выделившееся при трении.
Решение (продолжение)
Чтобы определить величину коэффициента трения, найдём работу силы трения, пользуясь определением работы.
|
s2 |
r r |
s2 |
|
|
A Fds |
F cos ds. |
||
F – сила, |
s1 |
|
s1 |
φ – угол между |
s – |
перемещение, |
|||
векторами силы и перемещения.
Чтобы найти силу трения, запишем второй закон Ньютона:
ma N mg Fтр
Величина силы трения скольжения Fтр = μN. В проекциях на оси координат (см. |
|
рисунок): |
max mg sin N, |
|
|
|
0 mg cos N. |

А3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной
плоскости высотой h = 0,5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2,45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q, выделившееся при трении.
Решение (продолжение)
max mg sin N, 0 mg cos N.
Из второго уравнения системы: N mg cos .
Величина силы трения |
Fтр N mg cos . |
|
|
|
s2 |
|
|
Работа силы трения |
A F cos ds |
Fтр |
l cos . |
|
s1 |
|
|
Угол между векторами силы трения и перемещения φ = 1800, cos1800= -1.
A Fтр l cos mg cos l.

А3. Тело массой m = 3кг, имея начальную скорость 0 = 0, скользит по наклонной
плоскости высотой h = 0,5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2,45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q, выделившееся при трении.
|
|
|
|
|
|
|
|
Решение (продолжение) |
|
|
|
|
|
|
|
||||||||||
A |
|
|
mv2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
mgh mg cos l. |
|
|
|
|
|
|
|||||||||||
тр |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
v2 |
gh g cos l, |
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
gh |
|
2gh v2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
. |
|
|
|
|
|
|
|||||||||
|
|
|
g cos l |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
2gl cos |
|
|
|
|
|
|
|||||||||||
cosα найдём из геометрических соображений: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
x |
|
|
|
|
|
l2 |
h2 |
|
|
2gh v2 |
|
|
2gh v2 |
|||||||||
cos |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
0, 22. |
||||
|
l |
|
|
l |
2gl cos |
|
2g |
l2 h2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|||||||||||||
Ответ: Q = -5,7 Дж, μ = 0,22.
А4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с относительно льда. На какое
расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = |
|||||||||
0,02? |
|
|
|
Решение |
|
||||
Дано: |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
Скорость, |
которую |
|
приобретёт |
|||||
|
|
||||||||
M = 70 кг |
|
|
|||||||
|
конькобежец, бросив камень, найдём из |
||||||||
m = 3 кг |
|
||||||||
|
закона сохранения импульса. Запишем |
||||||||
= 8 м/с |
|
||||||||
|
закон |
сохранении |
импульса |
в |
|||||
= 0,02 |
|
||||||||
|
лабораторной системе отсчёта. |
|
|||||||
|
|
|
|
||||||
s - ? |
|
|
|||||||
|
|
|
0 mv Mu. |
|
|||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
В проекции на ось OX (см. рисунок) |
|
||||||||
0 mv Mu.
Отсюда величина скорости конькобежца после броска
u mvM .
Рассмотрим движение конькобежца после броска. Второй закон Ньютона:
|
Ma Mg N Fтр . |
OX : |
Ma Fтр , |
OY : |
0 mg N. |

А4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0,02?
Решение (продолжение)
OX : |
ma Fтр , |
OY : |
0 Mg N. |
Величина силы трения скольжения
|
Fтр N. |
N Mg, |
Fтр Mg. |
Изменение полной механической энергии конькобежца равно работе неконсервативных сил, то есть работе силы трения.
E Aтр , |
E Ek U , |
|
U 0, |
E |
A . |
|||
|
|
kтр |
||||||
E |
Mv2 |
Mv2 |
Mu2 |
|
Mu2 |
. |
|
|
2 |
1 0 |
|
|
|
|
|||
k |
2 |
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
||||
Aтр Fтр S cos , |
, |
|
Aтр Fтр S cos |
MgS. |
||||

А4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0,02?
Решение (продолжение)
Ek Mu2 |
, |
|
Aтр |
MgS, |
|
||
2 |
|
|
|
|
|
|
|
E A , |
|
|
Mu2 |
MgS. |
|
||
|
|
|
|||||
тр |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
Отсюда |
|
|
|
S |
u2 |
. |
|
u2 |
2 gS, |
|
|||||
2 g |
|||||||
|
|
|
|
|
|
||
Подставим в последнюю формулу найденное ранее выражение для скорости конькобежца u:
|
mv |
|
|
|
|
|
u2 |
|
m2 v2 |
|
|
|
||||||||
u M |
|
, |
|
S |
|
|
|
|
|
. |
|
|||||||||
|
|
2 g |
M 2 |
2 g |
|
|||||||||||||||
Sм |
m2 |
|
|
|
v2 |
|
32 |
|
|
82 |
|
|
|
0,3 |
|
. |
||||
M 2 |
2 g |
702 2 0,02 |
9,8 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Ответ: S = 0,3 м.
