Энтропия
Круговые процессы Цикл Карно
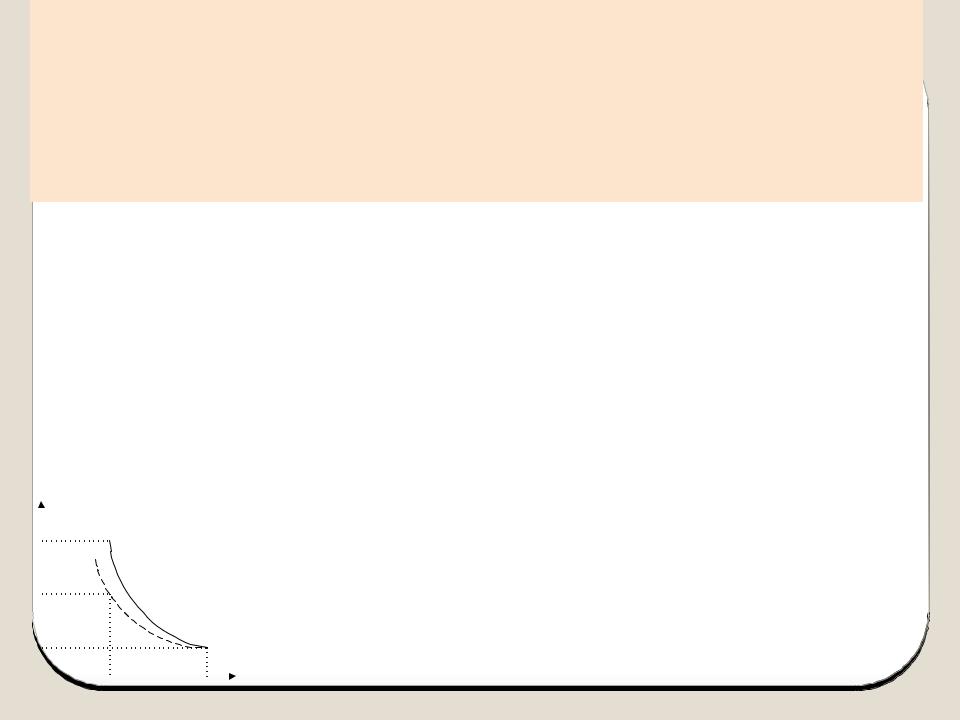
1. Двухатомный газ занимает объем V1=0,5 л при давлении Р1=50 кПа. Газ сжимается адиабатически до некоторого объема V2 и давления Р2 и затем при постоянном объеме V2 охлаждается до первоначальной температуры. При этом его давление становится
равным Р0=100 кПа. 1) Начертить график этого процесса; 2) Найти |
|
объем V2 и давление Р2. |
Р |
Дано
V1=0,5·10-3 м3 Р1=50·10+3 Па.
V2- ? Р2 - ?
По графику: переход 1- |
Р2 |
|
|
2 – адиабатический |
|
|
|
процесс, а переход 2-3 |
|
|
|
– изохорический. Точки |
Р |
|
|
1 и 3, |
|
0 |
|
|
|
|
|
соответствующие |
|
|
|
начальному и |
|
Р1 |
|
конечному состоянию |
|
||
лежат на изотерме |
|
|
|
(пунктирная линия), |
|
|
|
так как Т1=Т3. |
PV |
||
|
|||
|
1 |
1 |
|
2
3
1
V2 |
V |
V |
|
||
|
1 |
|
P2V2
1. Двухатомный газ занимает объем V1=0,5 л при давлении Р1=50 кПа. Газ сжимается адиабатически до некоторого объема V2 и давления Р2 и затем при постоянном объеме V2 охлаждается до
первоначальной температуры. При этом его давление становится равным Р0=100 кПа. 1) Начертить график этого процесса; 2) Найти
объем V2 и давление Р2.
|
PV P V |
PV P V |
|
|
V2 |
P1V1 |
|
|
P P (V1 ) |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
1 |
1 |
2 |
2 |
1 1 |
|
0 2, |
|
|
|
P0 |
|
2 |
1 |
|
|
V2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
P |
|
|
|
|
|
|
|
CP |
|
i 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P2 P1 ( |
0 |
) |
|
|
|
|
C |
|
|
|
|
|
|
|
|
1,4 |
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
P1 |
|
|
|
|
, |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
Р2 |
|
50 |
10 |
3 |
( |
100 103 |
) |
1,4 |
131,95 |
10 |
3 |
132 |
10 |
3 |
(Па) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
50 103 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Р2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3 |
|
|
|
|
|
V2 |
|
50 103 |
0,5 10 |
3 |
|
|
|
|
3 |
( |
м |
3 |
) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Р0 |
|
|
|
|
|
|
|
100 103 |
0,25 10 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Р1 |
|
|
|
1 |
|
|
|
|
|
Ответ: V2=0,25 10-3 м3; Р2=132 кПа. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
V2 |
V |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.(5.195) Идеальная тепловая машина, работающая по циклу Карно, получает за каждый цикл от нагревателя Q1=2512 Дж.
Температура нагревателя Т1=400 К, температура холодильника Т2=300 К. Найти работу, совершаемую машиной за один цикл, и
количество теплоты, отдаваемое холодильнику за один цикл. Ответ: А=630 Дж; Q2=1880 Дж.
Дано
Q1=2512 Дж
Т1=400 К Т2=300 К
А=? Q2=?
Решение
|
Т1 Т2 |
|
Q1 Q2 |
|
A Q1 Q2 |
||||||
|
, |
||||||||||
|
|
Т1 |
|
|
|
|
Q1 |
|
|
|
|
|
|
|
|
|
|
|
,. |
|
|
|
|
1 |
T1 |
|
A |
1 |
T2 |
1 |
Q2 |
||||
T2 |
Q1 |
T1 |
Q1 |
||||||||
Q2 2512 300400 1884( Дж)
A Q1 (1 T2 )
T1
Q2 Q1 T2 T1
A 2512(1 300400) 628( Дж)
3. Идеальная тепловая машина работает по циклу Карно. Определить КПД цикла, если известно, что за один цикл была произведена работа А=2,94 кДж и холодильнику было передано количество теплоты Q2=13,4 кДж.,
Дано |
|
|
|
Решение |
|
|
|
|
|
|||||
Т1 |
|
Т2 |
Q1 Q2 |
|
А |
|
||||||||
А=2,94∙103 Дж |
|
|
|
|||||||||||
Q1 |
||||||||||||||
Q =13,4 ∙103 |
|
|
Т1 |
|
Q1 |
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дж |
|
|
|
|
|
|
|
|
|
|
|
|
||
=? |
A Q1 Q2 |
|
Q1 A Q2 |
|||||||||||
|
|
|
||||||||||||
|
|
|
|
A |
|
A |
|
|
|
|
|
|||
|
|
|
|
A Q |
|
|
|
|
|
|||||
|
|
|
|
|
Q |
|
2 |
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
2,94 103 |
|
|
|
|
|
|
Ответ: η=18%. |
||||||
2,94 103 13,4 103 0,18 |
|
|||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
4.(5.198) Идеальная тепловая машина работает по циклу Карно. При этом 80 % теплоты, получаемой от нагревателя, передается холодильнику. Количество теплоты, получаемое от нагревателя Q1=6,28 кДж. Найти: 1) КПД
цикла; 2) работу А, совершенную за один цикл. Ответ: =20 %; А=1,26 кДж. .
Дано
Q2=0,8·Q1 Q1=6,28 ∙103 Дж
А=?
Решение
Q1 Q2 |
A Q1 Q2 |
Q1 |
|
A Q1 0,8Q1 |
0,2Q1 |
A 0,2 6,28 103 1,256 103 1,26(кДж)
Q1 0,8Q1 0,2
Q1
5.(5.216) Найти изменение энтропии при превращении массы
m=10 г льда, взятого при t =–20 |
.С, в пар при t =1000С. |
|
1 |
, |
3 |
Ответ: Дж/К. |
|
|
|
|
|
Дано
t1 200 C
t2 00 C
t3 1000 C
t2 00 C
C1 2,1 103 Дж кг К
С2 4,19 103 Дж кг К
3,35 105 Дж кг r 2,26 106 Дж кг
S ?
Решение
2 Q |
|
|
|
|
|
|
S T |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
S S1 S2 S 3 S4 |
|
|
|
|||
Q1 C1mdT |
S1 |
T2 C mdT |
C1m ln |
T |
||
|
T |
|
T |
|||
|
|
|
1 |
|
|
2 |
|
|
T1 |
|
|
|
1 |
|
|
|
|
|
|
|
Q2 m |
S2 |
Q2 m |
|
|||
|
|
T2 |
|
T2 |
|
|
,
|
|
, |
Q3 C2 mdT |
S3 |
, |
|
T3 |
C |
mdT |
|
T |
|
|
|
2 |
|
C2 m ln |
3 |
|
T |
T2 |
|||||
|
T2 |
|
|
|
|
|
Q4 mr |
|
S4 |
Q4 mr |
|
|
|
|
|
|
||||||||
|
|
|
|
|
T3 |
T3 |
|
|
|
|
|
|
|
||||
S m(C ln |
T2 |
|
|
С |
2 |
ln |
T3 |
|
|
r |
) |
|
|
||||
|
|
|
|
|
|||||||||||||
1 |
T1 |
|
T2 |
|
|
T2 |
|
|
T3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
S 0,01(2,1 103 ln 273 |
3,35 105 |
4,19 103 ln |
373 |
|
2,26 106 |
) |
|||||||||||
273 |
373 |
||||||||||||||||
253 |
|
273 |
|
|
|
|
|
|
|
|
|
||||||
88( Дж К)
6.(5.221) Найти изменение S энтропии при переходе массы |
|
|||||||||||||
m=6 г водорода от объема V1=20 л под давлением Р1=150 кПа к |
|
|||||||||||||
объему V2=60 л под давлением Р2=100 кПа. |
|
|
|
|
||||||||||
Ответ: S=71,0 Дж/К. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Дано |
|
Решение |
|
|
|
|
|
|
|
|
||||
m=6 г |
|
2 |
Q |
Q |
A dU pdV m CV dT |
|||||||||
V1=20 л |
|
S |
||||||||||||
Р1=150 кПа |
|
1 |
T |
|
|
|
|
|
|
|
|
|
|
|
V2=60 л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р =100 кПа |
|
|
|
V2 |
pdV |
T2 |
m |
|
dT |
|
|
|||
2 2 10 3 кг |
моль |
|
S |
|
|
|
|
|
||||||
|
|
|
T |
|
CV |
T |
|
|
||||||
S=? |
|
|
|
V |
|
|
T |
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
m |
|
|
m RT |
|
|
|
|
V2 |
m RT dV |
T2 |
dT |
|||
RT PV |
P |
V |
|
|
S |
|
V |
mCV |
||||||
|
|
|
|
T |
T |
|||||||||
|
|
|
|
|
|
|
|
|
V |
|
T |
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln a b |
ln a |
ln b |
|||||||||
S m R ln V2 m C ln T2 |
|
|
|
P1V1 |
|
|
P2V2 |
|
|
T2 |
P2V2 |
|||||||||||||||||||||||
|
|
|
V1 |
|
|
|
|
|
|
V |
T1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
P1V1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
T |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
S m R ln |
V2 m CV |
ln |
|
|
P2 |
m CV ln |
|
V2 m CV ln |
|
P2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
P1 |
|
|
|
|
|
V1 |
|
V1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m (C R)ln V2 |
||||||||||
S m[C ln |
|
P2 |
|
|
|
|
|
ln V2 |
|
|
|
|
|
|
|
|
V |
|
V1 |
|||||||||||||||
|
C |
|
|
|
] |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
V |
|
|
|
P |
|
p |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
R |
|
|
|
P2 |
|
|
|
|
|
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S |
2 |
i ln |
|
|
|
|
(i 2) ln |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
6 10 3 |
|
|
|
1 |
|
|
100 103 |
|
|
60 10 3 |
|
71,0( Дж |
|
|
|
|
||||||||||||||
|
|
S |
|
|
|
|
|
|
|
8,31 |
|
|
5ln |
|
|
|
7 ln |
|
|
|
|
К |
) |
|
|
|||||||||
|
|
2 |
10 3 |
|
|
150 |
103 |
20 10 3 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
7. Объем V1=1 м3 некоторого идеального газа, находящегося при температуре t=00С и давлении Р1=98 кПа, изотермически расширяется от объема V1 до объема V2=2V1. Найти изменениеS энтропии при этом процессе.
Дано
V1=1 м3 t=00С
Р1=98 кПаS=?
|
Решение |
|
|
|
|
|
|
|
|
||||
U 0 |
|
|
Q A pdV |
||||||||||
2 |
Q |
|
V2 |
pdV |
|
|
P |
|
m |
R |
|
||
S |
|
|
|
|
|
||||||||
|
|
|
T |
|
|||||||||
1 |
T |
|
V1 |
|
T |
|
|
V |
|||||
|
|
|
|
V2 |
|
|
|
|
|
V2 |
|||
|
S mR dV |
m R ln |
|||||||||||
|
V1 |
||||||||||||
|
|
|
|
|
|
V |
|
|
|
||||
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
7. Объем V1=1 м3 некоторого идеального газа, находящегося при температуре t=00С и давлении Р1=98 кПа, изотермически расширяется от объема V1 до объема V2=2V1. Найти изменение S энтропии при этом процессе.
V2 |
m |
|
dV |
|
m |
|
V2 |
m |
|
PV |
S |
R |
|
|
|
R ln |
|
|
R |
1 1 |
|
V |
|
V1 |
|
|||||||
V1 |
|
|
|
|
|
|
|
T |
||
S P1V1 ln V2 T . V1
S 98 103 1 ln 2V1 249( Дж К) 273 V1
S 249( Дж К)
8.(5.231) Изменение энтропии на; участке между двумя адиабатами в цикле Карно S=4,19. кДж/К. Разность температур между двумя изотермами Т=100 К. Какое количество теплоты Q превращается в работу в этом цикле?
Дано |
Процессы (1-2) и (3- |
|
S=4,19 кДж/К |
||
4) – изотермические, |
||
Т=100 |
а (2-3) и (4-1) – |
|
Q=? |
адиабатические. При |
|
адиабатических |
||
|
процессах изменение |
|
|
энтропии не |
|
|
происходит, а при |
|
|
изотермических: |
S12 Q1
T1
S
S2 3 |
|
2 |
|
S
4 |
|
1 |
|
|||
S1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Т |
|||
|
|
|
|
|
|
Т |
|
|
|
|
|
|
|
|
Т2 |
|
Т1 |
|||
S34 Q2
T2
A Q1 Q2 |
S12 T1 S34 T2 |
|
. |
Изменение энтропии за весь цикла Карно равно нулю
S12 S34 S
A S(T1 T2 ) S T
A 4,19 103 100 419 103(Дж)
A 419 103 ( Дж)