Динамика материальной точки
Применение второго закона Ньютона
А1. Молекула массой m = 4,65 10-26 кг, летящая со скоростью = 600 м/c, ударяется о стенку сосуда под углом = 600 к нормали и упруго отскакивает от нее без потери
скорости. Найти импульс силы , полученный стенкой за время удара.
Дано:
= 600 м/c m=4,65 10-26 кг=600
F t- ?
Решение
Используем второй закон Ньютона
r dp
F dt .
Импульсом силы называется величина
Fdt dp.
Найдём приращение импульса |
|
r |
r |
r |
|
|
|
dp p2 |
p1. |
|
|||
В проекциях на оси координат |
dp |
x |
p |
2x |
p |
, |
|
|
|
1x |
|
||
dpy p2 y p1y .
dpx p2x p1x p cos p cos 2mv cos . dpy p2 y p1y p sin p sin 0.
А1. Молекула массой m = 4,65 10-26 кг, летящая со скоростью = 600 м/c, ударяется о стенку сосуда под углом = 600 к нормали и упруго отскакивает от
нее без потери скорости. Найти импульс силы , полученный стенкой за время удара.
Решение (продолжение)
dpx p2x p1x 2mv cos .
Знак «-» у проекции на ось OX и равенство нулю проекции на ось OY означает, что приращение импульса и сила, действующая на молекулу, направлена «от стенки» (см. рис.). В то же время, сила, действующая на стенку со стороны молекулы, направлена в противоположную сторону.
r |
|
2mv cos 2 |
4,65 10 |
26 |
600 |
0,5 |
2,8 |
23 кг м |
|||
|
|||||||||||
Fdt |
|
|
10 |
|
|
. |
|||||
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
2,8 10 |
23 кг м |
||
|
|
. |
||
|
|
|
с |
|
|
|
|||
|
|
|
|
|
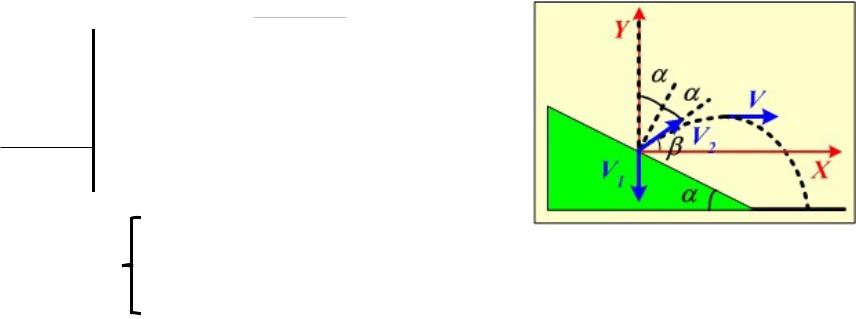
А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 300. За время удара шарик получает приращение импульса, модуль которого равен Δp = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории?
Дано:
m = 0,1 кг
Δp = 1,73 кг·м/с
= 300 t- ?
Решение
После удара о плоскость шарик движется в поле сил тяжести, его движение равномерное вдоль оси OX и равноускоренное с ускорением g вдоль оси OY. Кинематические уравнения движения:
x(t) x0 v0 cos t,
y(t) y0 v0 sin t gt22 .
В верхней точке траектории проекция скорости на ось OY равна нулю.
vy (t) dy |
|
d |
|
gt |
2 |
|
v0 sin gt. |
|
h v0 sin t |
|
|
||||
|
|
||||||
dt |
|
dt |
2 |
|
|
|
|
А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 300. За время удара шарик получает приращение импульса, модуль которого равен Δp = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории?
Решение (продолжение)
|
vy (t) v0 sin gt, |
vy (t) 0; |
|
|
v0 sin |
v0 sin gt 0; |
|
t1 |
время подъёма |
на максимальную |
|
|
g |
высоту. |
|
Удар упругий, следовательно, угол падения равен углу отражения и поэтому |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ; |
sin sin |
|
2 |
|
2 |
|
; |
|
|
|
|
||||||||
2 |
2 |
cos |
|
|
||||||
Отсюда |
|
|
|
|
|
|
|
|
||
|
t |
v0 sin v0 cos 2 . |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
1 |
g |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 300. За время удара шарик получает приращение импульса, модуль которого равен Δp = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории?
Решение (продолжение)
Скорость V0 найдём, рассмотрев удар шара о плоскость.
Удар упругий, поэтому модуль скорости остаётся неизменным.
|
|
|
|
|
|
|
|
V1 |
|
V2 |
|
|
V0. |
|
|
|
|
|
|
|
|
r |
|
|
|
|
px |
2 |
2 |
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
p |
|
|
|
|
|
py |
|
|
|
||||
px p2x p1x |
mv0 sin mv0 sin 0. |
|
|||||||||||||||
py p2 y p1y |
mv0 |
|
cos mv0 |
cos 2mv0 cos . |
|||||||||||||
|
r |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
p |
|
2mv0 cos |
. |
|
|
|
|
Отсюда |
|
v0 |
|
. |
||||
|
|
|
|
|
|
|
2m cos |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2. Шарик массы m = 0,1 кг, падая с некоторой высоты, ударяется о закреплённую наклонную плоскость и упруго отскакивает от неё. без потери скорости. Угол наклона плоскости к горизонту α = 300. За время удара шарик получает приращение импульса, модуль которого равен Δp = 1,73 кг·м/с. Какое время t пройдёт от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории?
Решение (продолжение)
Подставим полученное выражение для скорости в формулу для времени подъёма на максимальную высоту.
t |
|
v0 cos 2 |
p cos 2 |
|||||
1 |
|
|
g |
|
2mg cos |
|||
|
|
|
|
|
||||
t1 |
|
|
1,73 0,5 |
|
0,5 |
|||
|
|
|
|
|||||
2 |
0,1 9,8 |
0,866 |
||||||
|
|
|
|
|||||
.
c .
Ответ: 0,5 с.
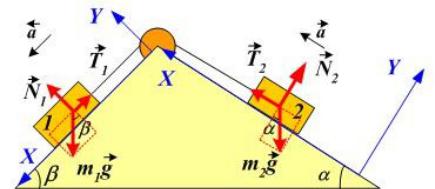
А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 300 и = 450 . Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены
нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь
Дано:= 30◦
= 45◦
m1 = m2 = 1 кг
T - ?
Решение
Если массой блока можно пренебречь, то ускорение
можно найти из второго закона Ньютона. Для тела 1:
r |
r |
r |
r |
m1a1 |
N1 |
T1 |
m1g. |
Предположим, что система движется справа налево на рисунке. Перепишем это уравнение в проекциях на оси (см. рис.) :
OX : |
m1a1 T1 m1g sin , |
OY : |
0 N1 m1g cos . |
Трения нет, поэтому ускорение первого тела определяется только проекциями сил на ось OX .
m1a1 T1 m1g sin . |
|
|
|
1 |
А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 300 и = 450 . Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены
нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь
|
|
|
|
Решение (продолжение) |
Уравнение второго закона Ньютона для тела 2: |
||||
r |
r |
r |
|
r |
m2a2 |
N2 |
T2 |
m2 g. |
|
Это же уравнение в проекциях на оси:
OX : |
m2a2 T2 m2 g sin , |
OY : |
0 N2 m2 g cos . |
Трения нет, поэтому ускорение первого тела определяется только проекциями сил на ось OX .
|
|
|
m2a2 |
|
T2 |
m2 g sin . |
|
|
|
|
2 |
|
||||||
Тела связаны нерастяжимой нитью, поэтому |
|
r |
|
|
|
r |
|
. |
|
|
||||||||
|
|
|
|
|
|
|||||||||||||
|
a |
|
|
a |
|
|
|
|||||||||||
|
r |
|
|
|
r |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
a. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обозначим |
a1 |
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
А3. Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы = 300 и = 450 . Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены
нитью и перекинуты через блок. Найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь
Решение (продолжение)
Если массой блока можно пренебречь, то согласно третьему закону Ньютона
|
|
|
|
|
T1 |
|
T2 |
. |
|||
Обозначим |
|
T1 |
|
|
|
T2 |
|
T. |
|||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Подставим введённые обозначение в (1) и (2):
m1a T m1g sin , m2a T m2 g sin .
Сложим первое и второе уравнения:
m1 m2 a m1g sin m2 g sin ,
a m1 sin m2 sin g. m1 m2