
физика / Mod1Pr1
.ppt
А6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?
Решение (продолжение)
Уравнения движения в полярных координатах:
z (t) 0t t2 . 2
z (t) 0 t.
Из второго уравнения выразим ε :
|
0 z (t) |
. Когда вентилятор остановится, |
z (t) 0. |
||||||||||
|
t |
|
|
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||
|
|
|
t2 |
|
|
|
|
t2 |
|
|
t |
|
|
|
z (t) 0t |
0t |
|
|
. |
||||||||
|
2 |
t |
0 |
2 |
0 |
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|||
0 2 0.
Когда вентилятор остановится, проекция углового перемещения составит
z 2 N. |
21 |

А6. Вентилятор вращается с частотой = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Какое время t прошло с момента выключения вентилятора до полной его остановки?
Решение (продолжение)
z (t) |
0t |
. |
0 2 |
0 . |
z 2 N. |
|||||
2 |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
2 N 2 0t . |
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
Время до остановки: |
t |
2N . |
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
||
|
0 |
900 |
|
об |
|
900 об 15 об . |
||||
|
|
мин |
||||||||
|
|
|
|
|
|
60 |
с |
с |
||
|
|
|
tс |
2N |
2 75 |
10( |
). |
|||
|
|
|
|
|
0 |
|
15 |
|
|
|
Ответ: t = 10 с. 22
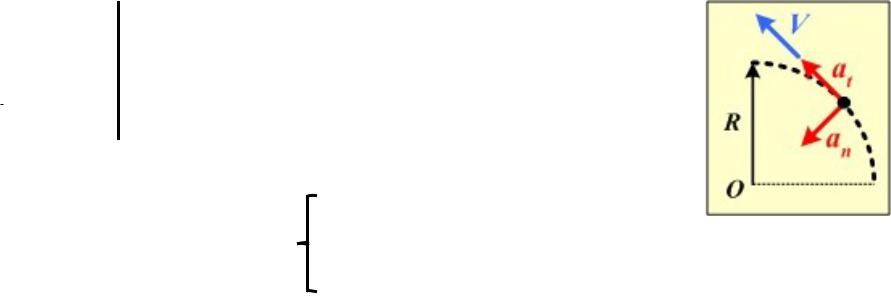
А7. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением а . Найти тангенциальное ускорение а точки, если известно, что к концу
пятого оборота после начала движения линейная скорость точки = 79,2 см/с.
Дано:
R = 20 см
а = const.= 79,2 cм/с
а - ?
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
Тангенциальная |
составляющая |
ускорения |
|
|
|
|||||||
направлена, как и вектор скорости, по касательной |
|
|
|
|||||||||
к траектории. Поэтому она «ответственна» за |
|
|
|
|||||||||
изменение |
|
модуля |
линейной |
скорости. |
|
|
|
|||||
Тангенциальная |
составляющая |
ускорения |
|
|
|
|||||||
постоянна по величине. |
|
a t |
2 |
|
|
|
|
|
||||
|
|
|
S v t |
|
, |
|
|
|
|
|||
|
|
|
|
t |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
2 |
|
|
|
|
|
|
||
|
|
|
v(t) v0 att. |
|
|
|
|
|||||
(S – путь, пройденный материальной точкой) |
|
|
|
|||||||||
t v(t) v0 |
, |
|
v0 0, |
t v(t) |
|
v |
, |
|||||
|
a |
|||||||||||
a |
|
|
|
|
|
|
|
|
a |
|
|
|
t |
|
|
|
|
|
|
|
|
t |
|
t |
|
S v t |
a t2 |
|
a t2 |
|
a v2 |
|
v2 |
|
|
t |
t |
t 0 |
0 |
. |
|
||||
|
|
||||||||
0 |
2 |
|
2 |
|
2a2 |
|
2a |
23 |
|
|
|
|
|
|
t |
|
t |
||

А7. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением а . Найти тангенциальное ускорение а точки, если известно, что к концу
пятого оборота после начала движения линейная скорость точки = 79,2 см/с.
Решение (продолжение)
|
S |
|
v2 |
|
|
|
at |
|
|
v02 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2S |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Путь, пройденный точкой, |
S 2 R N. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
N – число оборотов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
a |
|
v2 |
|
|
|
v2 |
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
t |
|
2S |
|
2 2 R N |
|
|
|
|
4 R N |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
|
|
v2 |
|
|
|
0,7922 |
|
|
|
|
0,05 |
м |
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
t |
|
4 R Nс 4 |
3,14 |
0, 2 |
5 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 0,05 |
м |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
с2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
||

А8. Колесо радиусом R=10 см вращается с угловым ускорением =3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость ; б) линейную скорость ; в) тангенциальное ускорение а ; г) нормальное
ускорение аn ; д) полное ускорение а; е) угол , составляемый вектором полного
ускорения с радиусом колеса. |
Решение |
|
|
|
|
|
|
|
|
||||||||||||
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
R=10 см |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Направления векторов |
скорости, |
|
угловой |
|||||||||||||||
|
=3,14 рад/с2 |
|
|
|
|||||||||||||||||
|
t = 1 с |
|
|
скорости и углового ускорения – на рисунке. |
|||||||||||||||||
|
|
|
Перейдём к полярным координатам. Колесо |
||||||||||||||||||
|
- ? |
|
|
||||||||||||||||||
|
|
|
движется с постоянным угловым ускорением. |
||||||||||||||||||
|
- ? |
|
|
||||||||||||||||||
|
|
|
Кинематическое уравнение движения: |
||||||||||||||||||
|
а |
- ? |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|||
|
а |
|
- ? |
|
|
|
|
z (t) 0z 0zt |
|
|
|||||||||||
|
|
n |
|
|
|
|
|
|
|
z |
. |
||||||||||
|
- ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Определим значения параметров уравнения: |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
0 z (t) 0; |
|
|
|
0z 0; |
|
|
z . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
z (t) |
t2 |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
Проекция угловой скорости колеса: |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
d z |
|
d |
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(t) |
|
t |
|
|
t. |
||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
dt |
|
dt |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

А8. Колесо радиусом R=10 см вращается с угловым ускорением =3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость ; б) линейную скорость ; в) тангенциальное ускорение а ; г) нормальное
ускорение аn ; д) полное ускорение а; е) угол , составляемый вектором полного
ускорения с радиусом колеса.
Решение (продолжение)
Проекция угловой скорости |
|
|
рад |
|
|
|
|
|
|
|
|
||||||
|
(t) t 3,14 1 3,14 |
|
|
|
|
|
|
|
|
||||||||
|
|
. |
|
|
|
|
|
|
|
|
|||||||
z |
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор линейной скорости |
|
|
|
|
|
|
|
|
|
|
|
||||||
, R . |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Направления векторов показаны на рисунке. Для модулей |
|
м |
|||||||||||||||
v |
|
R |
t R |
3,14 1 0,1 |
0,314 |
||||||||||||
|
|
|
|
|
|
. |
|||||||||||
z |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
с |
|
|||||
Тангенциальная составляющая ускорения |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a , |
R . |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
Направления совпадает с направлением вектора скорости. Для модулей |
|||||||||||||||||
|
|
|
a R 3,14 0,1 |
0,314 |
м |
|
|
||||||||||
|
|
|
|
|
|
|
|
. |
|
||||||||
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
с |
|
26 |
|||||

А8. Колесо радиусом R=10 см вращается с угловым ускорением =3,14 рад/с2. Найти для точек на ободе колеса к концу первой секунды после начала движения: а) угловую скорость ; б) линейную скорость ; в) тангенциальное ускорение а ; г) нормальное
ускорение аn ; д) полное ускорение а; е) угол , составляемый вектором полного
ускорения с радиусом колеса.
Решение (продолжение)
Нормальная составляющая ускорения направлена к центру окружности . Её величина
|
vм tR |
2 |
|
2 2 |
2 2 |
|
|
|
|
|
|||
a |
2 |
|
|
|
|
t R 3,14 |
1 |
0,1 |
1,0 |
|
|
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|||||||||
n |
R |
|
Rс |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Величину полного ускорения найдём по теореме Пифагора (см. рис).
a |
|
2 |
a |
2 |
|
2 |
0,314 |
2 |
1,05 |
м |
||
a |
|
|
1 |
|
|
|
. |
|||||
|
|
|
с2 |
|||||||||
|
n |
t |
|
|
|
|
|
|
||||
Нормальная составляющая ускорения направлена вдоль радиуса, тангенциальная – по касательной к окружности, поэтому угол между радиусом и вектором ускорения можно определить так:
tg |
at |
|
R |
|
R |
|
1 |
. |
arctg |
1 |
arctg |
1 |
18 . |
a |
2t2 R |
2t2 R |
|
t2 |
3,14 |
||||||||
|
|
|
|
t2 |
|
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
27

А9. Точка движется по окружности радиуса R = 1 м так, что зависимость криволинейной координаты, отсчитанной вдоль окружности, от времени задается уравнением s = A – Bt + Ct2, где В = 2 м/c и С = 1 м/c2. Найти линейную скорость точки, ее тангенциальное а ,
нормальное аn и полное а ускорения через время t = 3 с после начала движения.
Решение
Дано:
B = 2 м/с C = 1 м/с2 t1 = 3 c
R = 1 м
V - ?
an - ? at - ?
Проанализируем уравнение движения точки. При этом перемещение против часовой стрелки положительно, по часовой стрелке – отрицательно. s(t) A Bt Ct2.
Скорость, направленная по касательной к окружности
v(t) dsdt(t) dtd A Bt Ct2 B 2Ct.
Тангенциальное ускорение
t |
|
dv(t) |
|
dм |
|
|
|
|
2 |
|
|
|||
(t) |
|
|
|
|
|
Bt 2Ct |
2C 2 |
|
|
|
||||
a |
|
|
|
|
|
|
|
|
. |
|
||||
dt |
|
dtс |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
По условию B = 2 м/с, С = 1 м/с2, v(t) B 2Ct 2 2t. |
|
|||||||||||||
|
|
|
|
v(t) 0, при t 1(c). |
|
|
|
|
|
|||||
1. При t 1c |
v 0. |
См. рис 1. |
|
|
2. |
|
При t 1c |
v 0. См. рис282. |
||||||

А9. Точка движется по окружности радиуса R = 1 м так, что зависимость криволинейной координаты, отсчитанной вдоль окружности, от времени задается уравнением s = A – Bt + Ct2, где В = 2 м/c и С = 1 м/c2. Найти линейную скорость точки, ее тангенциальное а ,
нормальное аn и величину полного а ускорения через время t = 3 с после начала движения. Решение (продолжение)
Момент времени t = 3 c соответствует ситуации,
показанной на рис. 2.
v(t) B Ct 1 1 3 1 м .с
|
|
м |
|
|
|
|
|
vм |
|
|
|
|
|
|
||||||
a (t) 2C 2 |
|
|
|
|
. |
|
|
a (t) |
2 |
1 |
|
|
|
|
|
. |
||||
|
2 |
|
|
|
|
|
2 |
|||||||||||||
t |
|
|
|
|
|
n |
|
|
Rс |
|
|
|||||||||
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Величина полного ускорения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
2 |
|
2 |
|
2 |
|
|
м |
|
||||||
|
a |
|
an |
at |
|
1 |
2 |
|
2, 2 |
|
|
|
|
|
|
. |
||||
|
|
|
с2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
29

А10. Во сколько раз нормальное ускорение аn точки, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения а для того момента, когда вектор полного ускорения точки составляет угол = 30° с вектором ее линейной скорости?
Дано: |
Решение |
|
= 30° |
r |
r |
tg |
an |
|||
|
|
an at , следовательно, |
|
. |
|||
аn/ а - ? |
|||||||
|
|||||||
|
|
|
|
|
at |
||
an tg tg30 0,58. at
Ответ: an 0,58.
at
30
