Электрическое поле в веществе

1. Общее представление о диэлектриках

Термин «диэлектрик» впервые ввел М.Фарадей Согласно М. Фарадею внешнее электрическое поле проникает внутрь диэлектрика и проходит сквозь него в отличие от металлов, у которых внешнее поле полностью экранируется перемещением свободных электрических зарядов.

Количественно к диэлектрикам относят вещества, удельная электропроводность которых меньше 1 Ом-1см-1, к проводникам – вещества с удельной электропроводностью больше 1 Ом-1см-1. В диэлектриках в идеальном случае нет свободных зарядов, положительные и отрицательные заряды связаны друг с другом в пределах одной молекулы.

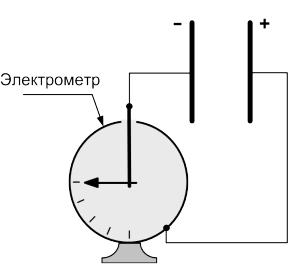
Рассмотрим опыт( рис.1).

1

Рис.1

Две рядом заряженные металлические пластины, закреплены на изолирующих подставках, образуя воздушный конденсатор. Пластины соединяются с электрометром. Электрометр показывает большой заряд. Если между обкладками этого конденсатора внести пластину из диэлектрика (стекло, эбонит, парафин), то показания электрометра уменьшаются. Если диэлектрик удалить, то показания электрометра увеличиваются, что указывает на уменьшение или увеличение разности потенциалов на обкладках конденсатора (рис.2).

Обсудим результаты опыта. Уменьшение разности потенциалов U означает уменьшение напряженности электрического поля Е между пластинами конденсатора, так как в данном случае

где d расстояние между пластинами конденсатора.

Рис.2

2

Известно, что статическое электрическое поле порождается электрическими зарядами и следовательно уменьшение напряженности должно указывать на уменьшение электрического заряда. Тогда в отсутствии диэлектрика силовые линии конденсатора(рис. 3а).

Рис. 3а

Уменьшение напряжённости происходит из-за того, что на поверхности диэлектрика появляются свои связанные заряды смещенные на поверхность под действием электрического поля (рис.3б,в)

3

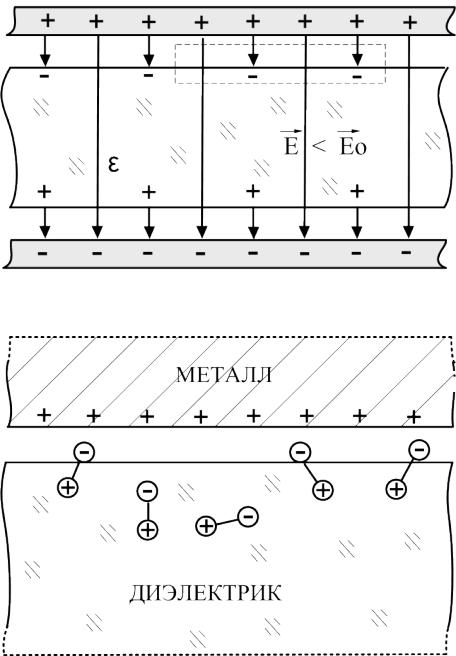
Рис.3б

4

Рис.3в

В результате этого силовые линии напряжённости поля конденсатора замыкаются на зарядах диэлектрика.

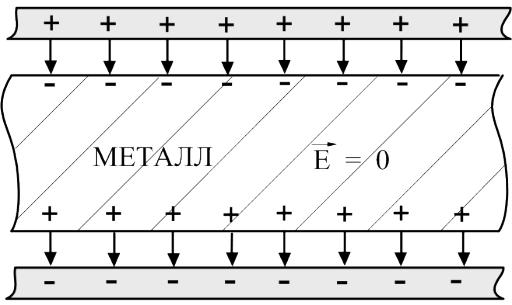
Смещенных на поверхность связанных зарядов меньше чем зарядов на металлических обкладках поэтому диэлектрик лишь ослабляет электрическое поле между пластинами, в отличие от металла, внутри которого поле будет равно нулю (рис.3г).

Рис. 3г.

5

2. Электрическое поле диполя

Рассмотрим электрическое поле, создаваемое диполем. Будем считать диполь точечным, если r. Напряженность поля диполя вычисляется как векторная сумма полей, создаваемых каждым зарядом диполя в данной точке.

а) точка наблюдения находится на оси диполя (рис.5)

Рис.5

Напряженность электрического поля

7

б) Точка наблюдения находится на прямой перпендикулярной оси диполя и проходящей через его середину (рис.6)

8

Рис.6

Напряженность диполя, согласно геометрии рисунка

9

в) в общем случае (рис.7) модуль напряженности поля диполя в точке наблюдения на расстоянии r от диполя определяется формулой

(9)

0

2

формула (9) переходит в полученные ранее формулы (4) и (7), соответственно.

10