Книги / Книга Проектирование ВПОВС (часть 2)

относится к каждому ПЭ. На рис. 5.18 показана векторная вычислительная структура, содержащая М обычных цифровых интеграторов, каждый из которых содержит N-процессорных элементов. Процессорные элементы,

принадлежащие одному интегратору, в соответствии с сформулированными выше требованиями, должны объединяться с 4-шинной сегментированной магистралью. На рис 5.19 она для простоты изображена одной линией.

Одноименные ПЭ различных интеграторов объединены через коммутатор и образуют узловой процессор.

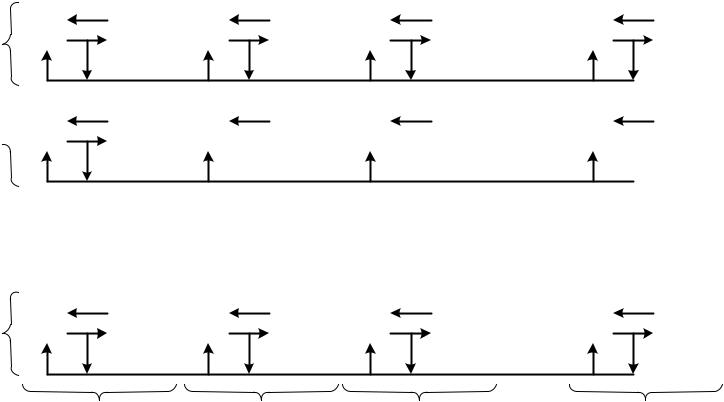
По аналогичному правилу можно организовать и двухмерную структуру. Двухмерная структура с узловым распараллеливанием показана на рис.5.19. Кружочками с индексом r1 обозначены процессорные элементы,

принадлежащие обобщенным цифровым интеграторам по направлению x1, а с индексом r2 – направлению x2. Все процессорные элементы r = r1+ r2

объединяются через полнодоступный коммутатор и образуют матричный узловой процессор. Все r процессорных элементов узлового процессора участвуют в реализации системы (1.42). Однако такой подход к построению вычислительной структуры обладает существенным недостатком,

заключающимся в том, что система не в состоянии адаптироваться к исходной задаче.

Векторная структура с узловым распараллеливанием показана на рис. 5.18.

312

Рис. 5.19

Действительно, пусть исходная система содержит N уравнений и из них

R операций обобщенного интегрирования или дифференцирований по

реализована структурно, хотя по общему числу элементов ограничения нет.

Для устранения этого противоречия, по аналогии с векторной структурой,

необходимо, чтобы число магистралей по каждому ив направлений x1 и x2

было равным числу ПЭ. В этом случае каждый из ПЭ должен иметь возможность подключения к одной из магистралей по направлению x1 или x2.

Это позволяет оперативно перераспределять ПЭ между каждой из направлений. В результате для решения задачи достаточно выполнить условие r N (количество ПЭ в узловом процессоре должно быть больше или равно исходной системе уравнений).

Указанная методика распространяется и на системе произвольной мерности. В этом случае ПЭ дополнительно снабжается либо коммутатором выбора направления (рис. 5.20 а), либо 4l – входовой памятью, где l –

314

ПЭ с буферной памятью и коммутатором направления на

мультиплексорах.

Рис. 5.20, б

Процессорный элемент с многовходовым буфером на входе показан на рис. 5.20, б.

При наличии памяти на входе ПЭ число ячеек для хранения данных в одном ПЭ равно (4rp), так как при неординарном соединение на вход одного ПЭ могут поступить одновременно данные из всех ПЭ. Тогда общее число ячеек равно

помощью буферной памяти на входе ПЭ предпочтительнее.

Схема узлового процессора с коммутирующей буферной памятью на входах ПЭ показана на рис. 5.21. Следует, однако, отметить, что при большом числе ПЭ значительно растет число шин (r*p). При этом каждая шина передачи бита требует отдельного мощного шинного формирователя. В

результате, с одной стороны, возрастает потребляемая мощность, а с другой – надежность системы резко падает из-за взаимного влияния шин друг на друга

316

318

Рис.5.21

318

В случае, когда число передаваемых данных значительно больше их

базовым при построении систем большой размерности.

Полученные результаты могут быть положены в основу анализа системы передачи данных между узловыми процессорами. Этот анализ показывает, что и в этом случае целесообразна передача последовательным кодом. Из системы уравнений Шеннона следует, что наряду с коммутацией должно осуществляться суммирование поступающих данных. В общем случае необходимо суммировать переменные, формируемые во всех ПЭ, а так как суммирование переменных производится последовательно друг за другом,

следовательно, необходимо устройство для хранения информации на период выполнения операции. С целью сокращения оборудований на это устройство можно возложить операцию коммутации между ПЭ. Преобразуем алгоритм работ узлового процессора таким образом, чтобы сохранив все положительные свойства, обеспечиваемые буфером, существенно уменьшить объем требуемого