ЭиУСУ / ЛИТЕРАТУРА_ЭиУСУ / Глазырин - МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ

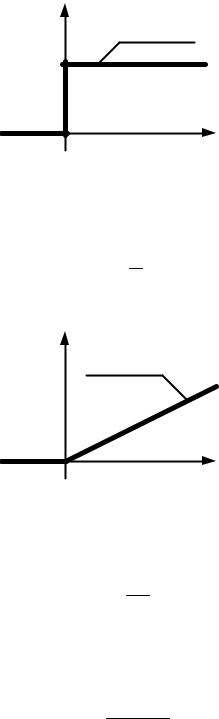
1.4.4. ИзображенияпоЛапласустандартных заводок электромеханическихсистем

(ступенька, линейное, гармоническое)

Единичное ступенчатое входное воздействие на ЭМС изображено на рис. 4.

Рис. 4. Ступенчатое входное воздействие

По таблице преобразований Лапласа для функции f (t) =1(t) имеем

следующее изображение:

F( p) = 1p .

Линейное воздействие на ЭМС изображено на рис. 5.

По таблице преобразований Лапласа для функции f (t) = a t имеем следующее изображение:

F( p) = pa2 .

Гармоническое воздействие на ЭМС изображено на рис. 6.

По таблице преобразования Лапласа для функции f (t) =sin(ω t)

имеем следующее изображение:

F( p) = p2 ω+ω2 .

21

Рис. 6. Гармоническое входное воздействие

Используя стандартные входные воздействия (заводки) ЭМС с использованием математических моделей, можно определить такие динамические показатели, как добротности по положению, скорости, моменту, скоростные и позиционные ошибки и т. д.

1.4.5. ПреобразованияпоЛапласусистемдифференциальных уравнений, описывающихэлектромеханическиесистемы

сненулевыминачальнымиусловиями

Предположим, что ЭМС описывается неоднородной СДУ в нормальной форме Коши:

Применим к СДУ прямое преобразование Лапласа. Учитывая теорему дифференцирования оригинала

f ′(t) p F( p) − f (0),

22

Перенесем слагаемые с неизвестными в левую часть СЛАУ, а свободные члены – в правую:

При нулевых начальных условиях данная СЛАУ выглядела бы следующим образом:

Преобразование Лапласа позволяет учесть начальные условия на самом первом этапе решения СДУ, при этом полученная СЛАУ ненамного отличается от той же СЛАУ при нулевых начальных условиях. В этом заключается одно из существенных преимуществ операторного метода решения СДУ перед классическим, в котором для учета начальных условий и нахождения постоянных интегрирования составлялась

ирешалась отдельная СЛАУ.

1.5.Решение систем дифференциальных уравнений

сприменением специальных теорем

Втех случаях, когда входное воздействие ЭМС имеет сложный вид, т. е. не является функцией Хевисайда, линейной или гармонической функцией, для решения СДУ с нулевыми начальными условиями удобно использовать специальные теоремы, к которым относятся интеграл Дюамеля и теорема Бореля. Эти два метода позволяют решить ДУ со сложной правой частью без нахождения ее изображения.

Применение специальных теорем основано на нахождении единичной переходной функции в случае использования интеграла Дюамеля

иимпульсной переходной функции в случае использования теоремы Бореля.

23

Единичная переходная функция h(t) – это реакция динамической

системы на единичную возмущающую функцию Хевисайда 1(t) при нулевых начальных условиях.

Импульсная переходная функция K (t) – это реакция динамической системы на единичный возмущающий импульс δ(t) при нулевых на-

чальных условиях. Единичный импульс (дельта-функция Дирака) связан с функцией Хевисайда следующим соотношением:

δ(t) = d1(dtt) .

Соответственно импульсная и единичная переходные функции связаны аналогично:

K (t) = dhdt(t) .

Приведем алгоритмы решения ДУ с помощью специальных теорем.

1.5.1. ИспользованиеинтегралаДюамеля

Пусть дано ДУ n-го порядка со сложной функцией правой части f (t) и нулевыми начальными условиями:

an x(n) + an−1 x(n−1) +...+ a0 x = f (t); x(0) = 0, x′(0) = 0,..., x(n−1) (0) = 0.

Алгоритм решения этого ДУ с помощью интеграла Дюамеля:

1. Найти единичную переходную функцию h(t) , для чего необходимо решить задачу Коши для следующего ДУ:

шить полученное ДУ классическим или операторным методом при тех же нулевых начальных условиях.

2.Найти производную единичной переходной функции.

3.Решить задачу Коши для исходного ДУ при помощи формулы

x(t) = ∫t h′(τ) f (t −τ)dτ.

0

Для определения оригинала x(t), в случае применения интеграла Дюамеля, потребуется три этапа, а в случае использования теоремы Бореля достаточно выполнить два этапа. Рассмотрим алгоритм применения теоремы Бореля для решения ДУ.

24

1.5.2. ПрименениетеоремыБореля

Пусть дано ДУ n-го порядка со сложной функцией правой части f(t) и нулевыми начальными условиями:

an x(n) + an−1 x(n−1) +... +a0 x = f (t); x(0) = 0, x′(0) = 0,..., x(n−1) (0) = 0.

Алгоритм решения этого ДУ с помощью теоремы Бореля:

1. Найти импульсную переходную функцию K (t) . Для этого необ-

ходимо решить задачу Коши для следующего ДУ:

an K (n) +an−1 K (n−1) +... +a0 K =δ(t);

K (0) = 0, K′(0) = 0,..., K (n−1) (0) = 0.

2. Решить задачу Коши для исходного ДУ по формуле

Интеграл Дюамеля и теорема Бореля позволяют найти аналитические функции, описывающие реакцию линейных ЭМС на входные сигналы, имеющие сложную форму.

1.6.Решение систем дифференциальных уравнений

сприменением определителей Вандермонда

Весьма удобным методом анализа динамики ЭМС с нулевыми начальными условиями является метод определителя Вандермонда, имеющий следующий алгоритм:

1.Записать СДУ, описывающую ЭМС, в нормальной форме Коши.

2.Найтисобственныезначения λ1, λ2 ,..., λn матрицыкоэффициентовA.

3.Записать полный D и частные D1 (t) , D2 (t) ,..., Dn (t) определи-

тели Вандермонда:

25

4. Записать матричную функцию F(t):

Здесь E – единичная матрица, A – матрица состояния системы. 5. Найти временные характеристики по формуле

x(t) =[F(t) − E] A−1 B.

При решении СДУ методом Вандермонда определяющим является владение операциями над матрицами (сложение, вычитание, умножение друг на друга и на число, нахождение обратной матрицы). Поэтому ниже приведены в общем виде основные операции над матрицами второго и третьего порядков.

Пусть даны квадратные матрицы 2-го порядка:

Для того чтобы сложить две матрицы, нужно сложить их соответствующие элементы. При этом матрицы должны быть одного размера. Аналогично производится и вычитание матриц.

Для матриц второго порядка

Для матриц третьего порядка

26

Для того чтобы умножить матрицу на число, необходимо каждый элемент матрицы умножить на это число. Аналогично поступают при делении матрицы на число.

Например, для матрицы второго порядка умножение на некоторое постоянное число c будет выглядеть следующим образом:

Несколько сложнее производится операция произведения матриц друг на друга. Для того чтобы получить элемент Zij матрицы произведения Z =Q S , необходимо записать сумму произведений элементов

i-й строки первой матрицы на элементы j-го столбца второй матрицы. Для матриц второго порядка

... q11 s13 +q12 s23 +q13 s33

... q21 s13 +q22 s23 +q23 s33 .

... q31 s13 +q32 s23 +q33 s33

При возведении матрицы в некоторую степень необходимо умножить матрицу саму на себя необходимое количество раз.

Для того чтобы найти обратную матрицу от заданной матрицы Q, необходимо составить другую матрицу путем замены каждого элемента матрицы Q его алгебраическим дополнением, деленным на определитель матрицы Q, а затем транспонировать полученную матрицу.

Алгебраическим дополнением элемента qij матрицы Q называется

минор этого элемента (определитель матрицы, состоящий из элементов этой матрицы после вычеркивания элементов i-й строки и j-го столбца),

27

взятый со знаком «+», если сумма (I + j) – четное число, и со знаком «–», если (I + j) – нечетное.

Обратная матрица от матрицы второго порядка –

Напомним в конце раздела, посвященного методу решения СДУ с помощью определителей Вандермонда, что данный метод применим только к задачам с нулевыми начальными условиями.

28

2.МОДЕЛИ ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ

ИИХ ЭЛЕМЕНТОВ

2.1.Модели, описываемые дифференциальными уравнениями первого порядка

Моделями, описываемыми ДУ 1-го порядка, например, могут являться RL- и RC-цепи, используемые в качестве фильтров низких и высоких частот.

Схема коммутации RL-цепи на источник постоянного напряжения представлена на рис. 7.

Рис. 7. Схема коммутации RL-цепи на источник постоянного напряжения Е

Процессы, протекающие в цепи при замыкании ключа, описываются дифференциальным уравнением 1-го порядка, составленным по второму закону Кирхгофа:

E 1(t) = i(t) R + L didt(t) .

Схема коммутации RC-цепи на источник постоянного напряжения представлена на рис. 8.

Рис. 8. Схема коммутации RС-цепи на источник постоянного напряжения Е

29

Дифференциальное уравнение, составленное по второму закону Кирхгофа, описывает процессы в цепи после замыкания ключа:

E 1(t) = iC (t) R +UC (t).

Учитывая, что iC (t) = C dUdtC (t) , это уравнение можно записать

в следующем виде:

E 1(t) = RC dUdtC (t) +UC (t).

Как видно из моделей, переменными состояния в RL- и RC-цепях являются ток через катушку индуктивности и напряжение на конденсаторе соответственно.

2.2. Модели, описываемые дифференциальными уравнениями второго порядка

В качестве моделей, описываемых ДУ 2-го порядка, можно рассмотреть нагруженные RLC-фильтры низких и высоких частот, а также двигатель постоянного тока независимого возбуждения, являющегося основой ЭМС постоянного тока.

2.2.1. Фильтрнизкихчастот

Ненагруженный RLC-фильтр представляет собой последовательно соединенные резистор, катушку индуктивности и конденсатор. В зависимости от того, с какого элемента (индуктивности или емкости) будет сниматься напряжение в качестве выходного, фильтр может пропускать высокие или низкие частоты.

Схема коммутации нагруженного фильтра низких частот (ФНЧ) на источник постоянного напряжения представлена на рис. 9.

Рис. 9. Схема коммутации нагруженного ФНЧ 2-го порядка на источник постоянного напряжения

30