Лекции ДМ и ОК / ЛЕКЦИЯ 4

27

ЛЕКЦИЯ 4

Виды разрушения зубьев

В процессе зацепления на зуб действует нагрузка, передаваемая зацепление, и силы трения. Для каждого зуба напряжения изменяются во времени по прерывистому отнулевому циклу. Повторно-переменные напряжения являются причиной усталостного разрушения зубьев: их поломки и выкрашивания рабочих поверхностей.

Трение в зацеплении вызывает износ и заедание зубьев.

Поломка зуба. Наиболее опасный вид разрушения для открытых передач. Излом возникает за счет переменных напряжений изгиба и перегрузки.

Усталостное выкрашивание рабочих поверхностей зубьев  основной вид разрушения для закрытых передач. Возникает за счет повторно переменных контактных напряжений . Процесс разрушения начинается на ножке зуба в околополюстной зоне, где рзвивается наибольшая сила трения, способствующая пластичному течению металла и образованию микротрещин на поверхности зубьев. Развитию трещин способствует расклинивающий эффект смазки. При выкрашивании нарушаются условия образования сплошной масляной пленки, что приводит к быстрому износу и задиру зубьев.

Износ зубьев. По мере износа зуб утоньшается, ослабевает его ножка, что приводит к его поломке.

Заедание зубьев. Заключается в приваривании частиц одного зуба к другому вследствие местного повышения температур в зоне зацепления. Образовавшиеся наросты задирают рабочие поверхности зубьев.

Материалы зубчатых колес

Стали являются основным материалом для зубчатых колес. Они подвергаются термической обработке. По твердости стали делятся на две группы:

Первая группа  НВ350

Вторая группа > НВ350 (10НВ  1НRC)

Высокая твердость рабочих поверхностей достигается объемной и поверхностной закалкой, цементацией, азотированием, цианированием.

Стальное литье применяется при изготовлении крупных зубчатых колес.

Чугуны применяются при изготовлении зубчатых колес тихоходных открытых передач.

Пластмассы применяются в быстроходных малонагруженных передачах для шестерен, работающих в паре с металлическими колесами.

Допускаемые контактные напряжения

Для закрытых зубчатых передач основным, выполняемым в качестве проектного, является расчет на контактную прочность; расчет на изгиб выполняется как проверочный. Открытые передачи рассчитывают на изгиб.

Допускаемые контактные напряжения для расчетов на выносливость при длительной работе

(16.10)

, (16.11)

где ;  для базового числа циклов;  предел контактной выносливости поверхностей зубьев, определяются экспериментально.

Расчет прямозубых передач ведут по меньшему значению из полученных для шестерни и колеса.

Для косозубых передач рассчитывается осредненное контактное напряжение

(16.12)

где и - допускаемые контактные напряжения для шестерни и колеса. При этом не должно быть больше 1,23.

Допускаемые напряжения изгиба

Допускаемые напряжения изгиба для расчетов на выносливость при длительной работе

, (16.13)

где  предел выносливости зубьев по излому от напряжений изгиба, соответствующий базовому числу циклов N. Экспериментальные данные приводятся в соответствующих таблицах;  требуемый коэффициент безопасности - верхнее значение для литых колес; при базовом числе циклов , т.е. для длительно работающих передач.

Расчетная нагрузка

Расчетная нагрузка определяется как:

, (17.3)

где  номинальная нагрузка; K  коэффициент нагрузки, определяемый как:

. (17.4)

Коэффициентам , , приписывается индекс H (, , ) при расчете на контактную прочность и индекс F (,,) при расчете на изгибную прочность.

Коэффициент учитывает неравномерность распределения нагрузки между зубьями. При прямозубой передаче .

Коэффициент учитывает неравномерность распределения нагрузки по ширине венца зубчатого колеса. При постоянной передаваемой нагрузке неравномерность ее распределения можно полностью устранить, т. е. . В остальных случаях из таблиц.

Коэффициент учитывает действие динамических нагрузок в зацеплении.

В качестве средних значений принимают ; .

Цилиндрическая прямозубая передача

Силы в зацеплении

Силы взаимодействия между зубьями определяют в полюсе зацепления П.

Распределенную по контактным линиям нагрузку заменяют равнодействующей , которая направлена по нормали NN. Для расчетов силу раскладывают на: окружную силу и радиальную силу (рис. 17.1).

Рис. 17.1. Схема сил в прямозубой цилиндрической передаче

Окружная сила

, (17.1)

где T  вращающий момент.

Радиальная сила

. (17.2)

Расчет на изгиб цилиндрических прямозубых передач

Основным критерием работоспособности открытых передач является прочность зубьев на изгиб.

При выводе расчетной формулы принимают допущения:

1. Вся нагрузка передается одной парой зубьев.

2. Силу трения не учитывают.

3. Зуб рассматривают как консольную балку.

Перенося силу по линии ее действия в точку A (на ось зуба), разложим ее на окружную и радиальную (рис. 17.2).

Напряжение изгиба:

, (17.5)

где  изгибающий момент;  момент сопротивления в опасном сечении, т. е. у корня зуба.

Напряжение сжатия:

, (17.6)

где  площадь опасного сечения.

Опасное сечение расположено у корня зуба. Разрушение начинается в растянутой зоне.

Суммарное напряжение в точке B будет равно

. (17.7)

Умножив числитель и знаменатель на модуль, получим:

. (17.8)

Рис. 17.2. Схема расчета зубьев на изгиб

Обозначив  коэффициент прочности зуба по номинальным напряжениям;  коэффициент прочности зуба по местным напряжениям;  теоретический коэффициент концентрации напряжений принимается из таблиц.

Формула проверочного расчета на изгиб

. (17.9)

Заменив в (17.9) и и выразив модуль m, получим формулу проектного расчета на изгиб

. (17.10)

Для прямозубых передач рекомендуют , тогда

, (17.11)

где  вращающий момент на шестерне;  число зубьев шестерни;  допускаемое напряжение изгиба для материала менее прочного зубчатого колеса;  коэффициент ширины венца колеса выбирают из таблиц.

Расчет на контактную прочность

цилиндрических прямозубых передач

Основным критерием работоспособности закрытых зубчатых передач является контактная прочность поверхностей зубьев.

Наибольшее контактное напряжение в зоне зацепления определяют по формуле Герца:

, (17.12)

где  приведенный модуль упругости;  приведенный радиус кривизны;  Пуассона; q  нормальная нагрузка на единицу длины контактной линии зуба, длина которой для прямозубых передач равна ширине венца колеса .

Формула для проверочного расчета:

, (17.13)

где  коэффициент, учитывающий форму сопряжения поверхности (при );  коэффициент, учитывающий механические свойства материалов сопряженных колес (для стальных колес Па);  коэффициент, учитывающий влияние коэффициента торцевого перекрытия (для прямозубой передачи ).

Коэффициент распределения нагрузки между зубьями для прямозубой передачи .

С учетом этих значений коэффициентов получим формулу проверочного расчета цилиндрических прямозубых стальных передач:

. (17.14)

Произведем в (17.14) следующие замены: ; ; и получим

. (17.15)

Окончательно формула проектного расчета для закрытых цилиндрических прямозубых стальных передач:

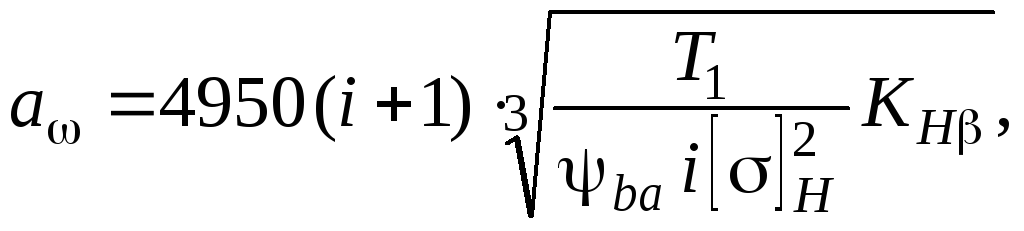(17.16)

где  межосевое расстояние, м;  вращающий момент на валу, Нм;  допускаемое контактное напряжение для менее прочного из материалов пары зубчатых колес, Па;  коэффициент ширины венца колеса.