Лекции ДМ и ОК / ЛЕКЦИЯ 5 Косозубая

32

ЛЕКЦИЯ 5

Цилиндрическая косозубая передача

Цилиндрические колеса, у которых зубья расположены под углом наклона линии зуба , называются косозубым (рис. 17.3).

У пары сопряженных косозубых колес углы  равны по величине, но противоположны по направлению.

Чем больше угол наклона , тем выше плавность зацепления, так как зуб входит в зацепление не сразу всей длиной, а постепенно.

Косозубая передача применяется в ответственных механизмах при средних и высоких скоростях.

Рис. 17.3. Геометрические размеры косозубого колеса

У косозубых колес расстояние можно измерять в торцевом (tt) и нормальном (nn) направлениях  окружной шаг;  нормальный шаг.

Различны в этих направлениях будут и модули

; (17.17)

, (17.18)

где  окружной шаг;  нормальный шаг.

Так как , то

. (17.19)

, (17.20)

где – d – делительный диаметр.

Эквивалентное колесо (косозубая цилиндрическая передача)

Профиль косого зуба в нормальном сечении АА соответствует исходному контуру инструментальной рейки, и следовательно, совпадает с профилем прямозубого колеса (рис. 17.4).

Рис. 17.4. Схема для определения z_v косозубого колеса

Прочность на изгиб косого зуба определяется его размерами в нормальном сечении, поэтому расчет косозубых колес ведут, используя параметры эквивалентного прямозубого колеса, полученного из следующих условий.

Делительная окружность косозубого колеса в нормальном сечении АА образует эллипс с радиусом кривизны в полюсе зацепления:

(17.21)

Профиль косого зуба в этом сечении практически совпадает с профилем прямого зуба эквивалентного колеса.

Диаметр делительной окружности эквивалентного колеса:

, (17.22)

где  эквивалентное число зубьев; z  действительное число зубьев косозубого колеса.

С увеличением угла  возрастает эквивалентное число зубьев , следовательно, повышается прочность косых зубьев.

Силы в зацеплении

В косозубой передаче сила раскладывается на три составляющие (рис. 17.5):

Рис. 17.5. Схема сил в косозубой передаче

Окружная сила

; (17.23)

Радиальная сила

; (17.24)

Осевая сила:

. (17.25)

Осевая сила дополнительно нагружает подшипники с возрастанием угла , поэтому .

Расчет на изгиб цилиндрических косозубых передач

Вследствие наклонного расположения зубьев в косозубом зацеплении одновременно находится несколько пар зубьев, что уменьшает нагрузку на один зуб, повышая его прочность. Наклонное расположение зубьев увеличивает их жесткость на изгиб, уменьшает динамические нагрузки. Все эти особенности трудно учесть при выводе расчетных формул, поэтому расчет на прочность косозубых передач ведут по формулам эквивалентных прямозубых передач с введением в них поправочных коэффициентов. По условиям прочности габариты косозубых передач получаются меньше, чем прямозубых.

Проектный расчет. Аналогично расчету прямозубой передачи нормальный модуль зацепления

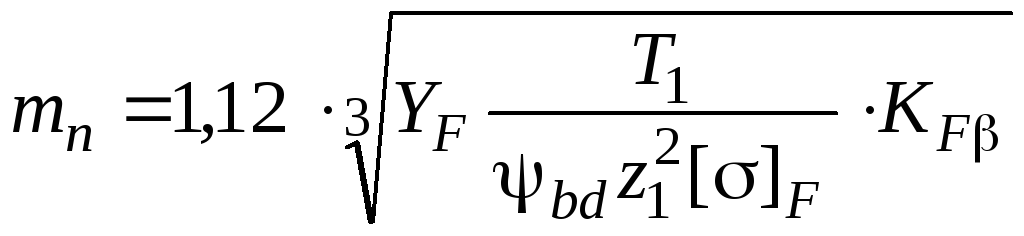, (17.26)

где дополнительно  коэффициент формы зуба выбирают по таблицам по эквивалентному числу зубьев .

В формулу (17.26) подставляют меньшее из двух отношений , вычисленных для шестерни и колеса.

Проверочный расчет. Аналогично расчету прямозубой передачи напряжения изгиба в зубьях

, (17.27)

где дополнительно  коэффициент, учитывающий перекрытие зубьев. По ГОСТ 2135475 для косозубых передач ;  коэффициент, учитывающий наклон зуба. При среднее значение .

Следовательно,

. (17.28)

Расчет ведут по менее прочному зубу, у которого меньше отношение .

Расчет на контактную прочность

цилиндрических косозубых передач

Проектный расчет. Аналогично расчету прямозубой передачи межосевое расстояние для стальной косозубой пары

. (17.29)

Проверочный расчет. Аналогично расчету прямозубой передачи контактные напряжения в поверхностном слое косых зубьев

, (17.30)

где дополнительно по ГОСТ 21354—75:

 коэффициент, учитывающий форму сопряженных поверхностей зубьев. Среднее значение ; Па^1/2  для стальных колес;  коэффициент, учитывающий перекрытие зубьев. Среднее значение . Следовательно,

, (17.31)

где  коэффициент, учитывающий распределение нагрузки между зубьями. Для косозубых колес при м/с для 68-й степеней точности, ;  коэффициент неравномерности нагрузки по ширине венца;  коэффициент динамической нагрузки. Для косозубых передач рекомендуется при любой твердости зубьев и м/с;  при твердости зубьев  НВ350 и м/с;  при твердости зубьев > HВ350 и м/с.