3.3. Решение статической (прочностной) задачи огнестойкости для железобетонных конструкций

3.3.1. Сжатые конструкции

Расчет огнестойкости центрально-сжатых конструкций выполняют по изменению несущей способности () во время нагрева рабочей части поперечного сечения колонны («ядра») и рабочей арматуры.

Последовательность расчета фактического предела огнестойкости П_ф центально-сжатых железобетонных конструкций

1. Задаемся интервалами времени _1…_n.

2. Для заданных интервалов времени определяем температуру стержней.

3. По найденным температурам из п. 3.1.5. [5] находим коэффициент _s,tem.

4. Находим размеры ядра сечения b_я и h_я для заданных промежутков времени.

5. Определяем несущую способность колонны в заданные промежутки времени.

6. Строим график снижения несущей способности колонны в условиях пожара и определяем П_ф при N_{p, t} = N_n.

Несущая способность нагретой железобетонной колонны при обогреве с 4-х сторон определяется по формуле:

(3.28)

где А_я – площадь ядра сечения,

А_я = b_яh_я

b_я = b - 2δ_x, где δ_x – слой бетона прогретый до критической температуры по оси X,

h_я = h - 2δ_y, где δ_y – слой бетона прогретый до критической температуры по оси Y;

A_{s, tot} – суммарная площадь арматуры;

_tem – коэффициент продольного изгиба, учитывающий длительность загружения, гибкость и характер армирования колонн (п. 3.2.10 [5]);

нормативные сопротивления бетона R_bn (п. 3.2.1 [5]) и арматуры R_sn (п. 3.1.2 [5]) определяются по СНиПу 2.03.01.-84* «Бетонные и железобетонные конструкции» в зависимости, соответственно от класса бетона и арматуры;

R_bu = R_bn/0,83 и R_scu = R_sn/0,9.

Y al

δ_y

δ_x

b X

A_{s, tot} h

Рис. 3.3. Сечение колонны

3.3.2. Изгибаемые конструкции

При работе изгибаемых конструкций бетон сжатой зоны попереч­ного сечения конструкции воспринимает сжимающие усилия, а несущие арматурные стержни в растянутой зоне - растягивающие усилия, со­ответственно. При этом соблюдается равенство воспринимаемых уси­лий (равновесие сил: ΣP = 0).

При нагреве конструкции сопротивление арматурной стали рас­тяжению уменьшается. Арматура претерпевает пластические деформа­ции ползучести, что приводит к раскрытию трещин в бетоне растяну­той зоны и, соответственно, уменьшению высоты (x_t) сжатой зоны конструкции (при этом вводится допущение, что сопротивление бето­на сжатию в этой зоне равно начальному и не меняется при нагреве, а меняется x_t).

Предел огнестойкости статически определимых изгибаемых конс­трукций наступает в результате прогрева несущей арматуры в растянутой зоне конструкции до критической температуры (t_s,cr) и образования пластического шарнира в середине пролета конструкции, ха­рактеризующего утрату ее несущей способности. Поэтому решение статической части задачи огнестойкости сводится к определению величины (t_s,cr).

При этом величину (t_s,cr) определяют по справочным (экспериментальным) данным (п. 3.1.5 [5]) в зависимости от значения коэффициента изменения прочности стали (γ_s,t,cr), соответствующего величине (t_s,cr). Величина (γ_s,t,cr) характеризует момент снижения сопротивления арматурной стали (R_sutcr), нагретой до критической температуры, до величины рабочего напряжения в арматуре (σ_s) от нормативной нагрузки на конструкцию. Поэтому при критической тем­пературе арматуры справедливо равенство (R_sutcr = σ_s). Это позво­ляет в формулу расчета (γ_s,t,cr ) вместо величины (R_sutcr) подставлять (σ_s):

(3.29)

где r_sсu - расчетное сопротивление стали по пределу прочности, Па.

Рассмотрим особенности методики решения статической задачи огнестойкости для плоской изгибаемой конструкции. Ее несущая способность (M_t) в предельном равновесии сил будет равна:

(3.30)

где N_bt - несущая способность бетонной части сжатой зоны попереч­ного сечения конструкции, Н;

Z_bt - плечо внутренней пары сил от середины сжатой зоны попе­речного сечения конструкции до оси растянутой арматуры, м;

b - ширина конструкции (сжатой зоны), м;

x_t - высота сжатой зоны поперечного сечения конструкции, м.

h_o - рабочая (полезная) высота поперечного сечения конструк­ции (расстояние от оси растянутой арматуры до верхней границы сжатой зоны поперечного сечения конструкции), м;

R_bu - расчетное сопротивление бетона сжатию, Па:

(3.31)

где R_bn - нормативное сопротивление (призменная прочность) бето­на осевому сжатию (п. 3.2.1 [5]), Па;

- коэффициент надежности по бетону = 0,83.

В условиях пожара конструкция разрушится под действием изги­бающего момента (М_n) от внешней нормативной (рабочей) нагрузки на конструкцию; Это произойдет при уменьшении ее несущей способности (M_t) до (М_n), т.е. при (M_t = M_n) или (M_t - M_n =0).

В развернутом виде это запишется:

(3.32)

отсюда

(3.33)

Учитывая равенство несущей способности бетона сжатой зоны и растянутой арматуры, в предельном равновесии сил напряжение в ар­матуре (σ_s ) от внешней нагрузки определяют по формуле:

(3.34)

где А_s - суммарная площадь поперечного сечения арматурных стерж­ней в растянутой зоне поперечного сечения конструкции (п. 3.1.1. [5]), м².

Затем можно вычислить (γ_s,t,cr) по формуле (3.29);

(t_s,cr) - по п. 3.2.5 [5] и (П_ф ) - по формуле (3.6).

Фактический предел огнестойкости плоских изгибаемых конструкций можно определить, как и для сжатых железобетонных конструкций, по графику снижения несущей способности в условиях пожара.

При этом на огнестойкость существенное влияние оказывает схема опирания конструкции:

• статически определимые (свободно-опертые) конструкции (рис. 3.4);

• статически неопределимые конструкции (рис. 3.5, 3.6).

Рис. 3.4. Схема статически-определимых изгибаемых железобетонных конструкций

Рис. 3.5. Схема статически-неопределимых изгибаемых железобетонных конструкций

Рис. 3.6. Схема опорного сечения статически-неопределимых изгибаемых железобетонных конструкций

Несущая способность статически определимых конструкций в условиях нагрева определяется:

(3.35)

(3.36)

(3.37)

Несущая способность статически неопределимых конструкций в условиях нагрева определяется:

(3.38)

- несущая способность пролетного сечения определяется по формуле (3.35) или (3.36).

Несущая способность опорного сечения (M_per(A),tem, M_per(B),tem) в условиях нагрева определяется по формуле:

(3.39)

x_tem – высота сжатой зоны, определяется по формуле (3.37).

Особенностью решения статической части задачи огнестойкости для многопустотных железобетонных плит и панелей является необхо­димость приведения формы их поперечного сечения к форме тавра (рис.3.7). При этом высота сжатой зоны может быть рассчитана по формуле (3.33), если (x_t ≤ h_f). В том случае, если (x_t > h_f), то формулу для расчета (x_t) получают из равенства (3.30), учитывающего разделение формы сжатой зоны на два прямоугольника.

b

b_p b_p b_p b_p b_p

h h₀

a

A_s

b´_f

x_tem≤h´_f

h´_f

h h₀

x_tem>h´_f

A_s

a ∑b_р

Рис.3.7. Расчет огнестойкости плоских изгибаемых многопустотных железобетонных элементов

Несущую способность вычисляют по формуле:

(3.40)

Отсюда

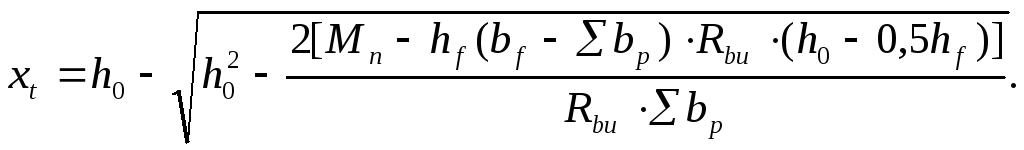(3.41)

Величину _s при (x_t ≤ h_f) определяют по формуле:

(3.42)

при (x_t > h_f):

(3.43)

Далее по формуле (3.29) вычисляют γ_s,t,cr, далее по п. 3.2.5 [5] находят t_s,cr, затем определяют (П_ф ) по формуле (3.6) и умножают на коэффициент 0.9, учитывающий влияние пустот плиты.

Последовательность

расчета предела огнестойкости плоских изгибаемых многопустотных железобетонных элементов

1. Вычисляется изгибающий момент M_n (в зависимости от нагрузки).

2. Вычисляется высота сжатой зоны x_tem по формуле:

3. Если , то _s,tem определяется по формуле

, где вместо b используется ;

Если , то ее необходимо пересчитать по формуле:

и тогда:

4. По 3.1.5 [5] определяется t_s,cr (критическая температура).

5. Вычисляется функция ошибок Гаусса по формуле:

7. По 3.2.7 [5] находится аргумент функции Гаусса.

8. Вычисляется предел огнестойкости П_ф по формуле:

При расположении арматуры, в сечении изгибаемой железобетонной конструкции, в два ряда (рис. 3.8), для расчета расстояния до центра тяжести растянутой арматуры необходимо пользоваться формулой:

(3.44)

где

а₁ и а₂ – расстояния до центра тяжести арматуры первого и второго ряда соответственно;

А_s1 и А_s2 – суммарная площадь арматуры первого и второго ряда соответственно (п. 3.1.1 [5]);

Рис. 3.8. Схема расположения арматуры в два ряда