Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Политехнический институт СФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

УМКД5 / ЗДиС / Методические пособия / Пособие по подготовке к практическим (2 раздел).doc

Скачиваний:

413

Добавлен:

01.06.2015

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Особенности решения теплотехнической задачи

Учитывая, что аналитическое решение дифференциального уравнения Фурье связано с громоздкими вычислениями, и невозможно выполнить без ЭВМ, в инженерной практике пользуются упрощенной методикой расчета, разработанной на основе уравнения Фурье с применением экспериментальных данных доктором технических наук, профессором А.И. Яковлевым [4].

Решение уравнения Фурье, полученное А.И.Яковлевым для полуограниченного тела, может быть использовано для определения температуры в плоских конструкциях конечной толщины.

В железобетонных конструкциях имеет место двумерное температурное поле при обогреве с трех и четырех сторон (балки, колонны) и одномерное температурное поле при обогреве с одной стороны (плиты).

При известном температурном поле могут быть получены сопротивления в бетоне в различных точках сечения элемента с определенными значениями температур.

Для расчета температур в сечении бетона примем следующие положения:

Значение теплоемкости и теплопроводности принимаются постоянными С_tem_,_m; _tem_,_m при некотором среднем значении температуры, которая принимается равной t_m= 450C.
Температурный режим принимается стандартным (ГОСТ 30247.0 – 94).

(3.1)

где:

t_b – температура в печи, соответствующая времени τ, C;

t₀ – температура в печи до начала теплового воздействия (принимается равной температуре окружающей среды), C;

τ – время, исчисляемое от начала испытания, мин.

Испытанием на огнестойкость установлено, что температура обогреваемой поверхности плоских железобетонных конструкций возрастает по кривой, уравнение которой имеет вид:

(3.2)

где: t₀ - температура обогреваемой поверхности,С;

t_н - начальная температура конструкции, С;

erf - функция ошибок Гаусса;

k - коэффициент, зависящий от плотности _0с сухого бетона, с^0,5;

 - время, с.

Расчет температур в сплошных плоских конструкциях

При одностороннем обогреве:

Температура в сечении конструкции рассчитывается по формуле:

(3.3)

где:

y - расстояние по нормали от обогреваемой поверхности до расчетной точки тела, м;

а_red- приведенный коэффициент температуропроводности:

(3.4)

где:

_tem_,_m - средний коэффициент теплопроводности при t = 450С, Вт/(мС);

С_tem_,_m- средний коэффициент теплоемкости при t = 450С, Дж/(кгс);

w_b - начальная весовая влажность бетона, %;

_0с- средняя плотность бетона в сухом состоянии, кг/м³.

Температура в арматурных стержнях рассчитывается по формуле:

(3.5)

где

y - расстояние от обогреваемой поверхности до края арматуры, м;

k, k₁ – коэффициенты зависящие от плотности бетона.

Из формулы (3.3) для одностороннего обогрева можно выразить толщину слоя прогретого до критической арматуры _ty, предполагая y = _ty_.

(3.6)

X (аргумент функции ошибок Гаусса) определяется по п.3.2.7 [2] в зависимости от

(3.7)

Пример №1:

Дано: железобетонная плита толщиной δ_пл = 80 мм. Бетон на гранитном щебне с объемной массой 2415 кг/м³, влажность бетона w_b= 3,5%, время «стандартного» огневого воздействия τ = 1 ч.

Требуется определить: температуру обогреваемой поверхности t₀, температуру арматурных стержней , толщину слоя бетона прогретого до критической температуры δ_t_,_y_.

Расчет:

Определим теплофизические характеристики бетона п. 3.2.3.[2]:

_0с = ₀– (₀ * w_b/ 100%) = 2415 – (2415*3,5/100) ≈ 2330 кг/м³;

_tem_,_m = 1,2 – 0,00035t = 1,2 – 0,00035 * 450 = 1, 0425 Вт/(мС);

С_tem_,_m= 710 + 0,84t = 710 + 0,84 * 450 = 1088 Дж/(кг·˚С);

Определим по формуле (3.2) температуру на обогреваемой поверхности:

Определим по формуле (5) температуру арматуры:

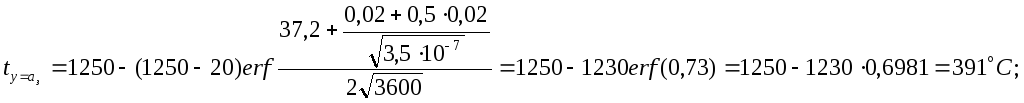Определим по формуле (3.6) толщину слоя прогретого до критической температуры:

Критическая температура бетона на гранитном щебне равна 650С.

Отсюда, по п.3.2.7. [3] X = 0,4635.

При трех и четырехстороннем обогреве:

Температура арматуры в стержневых конструкциях при обогреве с 3-х и 4-х сторон определяется по формуле (3.8):

(3.8)

где:

- температуры арматуры со стороны оси X и Y соотвественно, °С;

- изменение температуры при стандартном режиме пожара, °С (определяется по формуле 3.1.)

Если обогрев конструкции со всех четырех сторон, то:

(3.9)

(3.10)

где:

x, y – расстояние от обогреваемой поверхности до края арматуры, м;

k, k₁ – коэффициенты зависящие от плотности бетона [2];

d – диаметр арматуры, м;

h, b – размеры сечения;

τ – время, с.

Если обогрев конструкции с трех сторон, то там где одномерное поле (обогрев с одной стороны) температура арматуры определяется по формуле (3.5).

Слои прогретые до критической температуры определяются:

(3.11)

h_tem,y

h_я

b_я

b_tem,x

Рис. 3.2. Ядро сечения стержневых конструкций

Последовательность определения b_tem_,_x, h_tem_,_y

(3.12)

_х - определяется по графику (п.3.2.4. [2]) в зависимости от величины _х и F₀_x:

(3.13)

где t_y_=0,_ = 1250 - (1250 - t_н)_ц. (3.14)

_ц принимается по п.3.2.4. [2]) в зависимости от F₀_x/4.

(3.15)

Аналогично определяется:

(3.16)

Если обогрев конструкции с трех сторон, то там где одномерное поле (обогрев с одной стороны) слой бетона прогретый до критической температуры определяется по формуле (3.6).

Пример №2:

Дано: железобетонная колонна со случайным эксцентриситетом, сечением h×b = 300×300 мм. Обогрев с четырех сторон. Длина колонны 7,5 м. Класс бетона В30. Армирование 4Ø20 класса А-III. Защитный слой арматуры a_l = 25 мм. Время «стандартного» огневого воздействия τ = 1, 2, 3 ч. Бетон на гранитном щебне с объемной массой 2415 кг/м³, влажность бетона w_b= 3,5%.

Требуется определить: температуру арматурных стержней , толщину слоев бетона прогретых до критической температуры δ_t_,_x, δ_t_,_yв заданные промежутки времени огневого воздействия_.