Примеры решения задач

Пример 1. По контуру, изображенному на схеме, идет ток силой 10 А. Определить магнитную индукцию в точке О, если радиус дуги R = 10 см, α = 60^○.

Решение.В силу принципа суперпозиции магнитных полей магнитная индукцияв точкеОравна векторной сумме магнитных индукций, созданных всеми элементами контура с током. Разобьем весь контур на три участка – дугуАВи прямоугольные отрезкиВС,СА, чтобы для вычисления их магнитных полей можно было воспользоваться формулами для определения магнитной индукции в произвольной точкеАполя, созданного прямолинейным проводником с токомI(формула (1)), и для определения магнитной индукции в центре дуги окружности длинойLи радиусомR, обтекаемой токомI (формула (2)).

(1)

(2)

Здесь а– расстояние от точкиАдо проводника;φ₁иφ₂– углы, образованные радиусом-вектором, проведенным в точкуАсоответственно из начала и конца проводника.

Тогда получим

(3)

Сначала вычислим модули всех трех слагаемых. Поскольку угол α = 60^○, дугаАВсоставляет 1/6 часть окружности, т. е.L = 2πR/6=πR/3. Подставив это значение в формулу (2), найдем

(4)

Далее по формуле (1) определим величину В_ВС. На схеме видно, что углы, входящие в эту формулу,φ₁= 30^○,φ₂= 90^○. Расстояние от точкиОдо проводаВСестьа = ОС = R sin φ = R/2.Подставив значенияа,φ₁,φ₂ в формулу (1), имеем

(5)

Обратимся к уравнению, выражающему в скалярной форме закон Био –Савара – Лапласа, с помощью которого выведена формула (1).

(6)

Для любого элемента dlпроводникаСАугол, образованный этим элементом (взятый по направлению тока) и радиусом-вектором, проведенным от элемента в точкуО, равенπ. Следовательно,sin (dl,r) = 0. Однако при этом знаменатель формулы (6) отличен от нуля. Таким образом,dB = 0для любого элемента проводникаСА. Отсюда ясно, что и весь проводникСАне создает в точкеОмагнитного поля. Тогда соотношение (3) упростится:

(7)

Поскольку точка Ои контурАВСлежат в одной плоскости, оба вектора_АВ,_ВС, будучи перпендикулярными этой плоскости, оказываются расположенными вдоль одной прямой – нормали к плоскости чертежа, проходящей через точкуО. При этом, согласно правилу правого винта, вектор_АВнаправлен от наблюдателя, вектор_ВС– к наблюдателю. Приняв одно из этих направлений (например второе) за положительное, можно вместо (7) написать скалярное равенство

В = В_ВС – В_АВ

или, с учетом (4) и (5),

Подставив в эту формулу величины, выраженные в единицах СИ: I = 10 A,R = 0.1Ом,μ₀ = 4π  10^–7Гн/м, и произведя вычисления, получимВ = 6,9мкТ.

Пример 2. По двум длинным параллельным проводам текут в противоположных направлениях токи силой I₁ = I₂ = I =10 А. Расстояние между проводами а = 0.3 м. Определить магнитную индукцию в точке А, удаленной от первого и второго проводов соответственно на расстояния а₁=0.15 м, а₂ = 0.2 м.

Р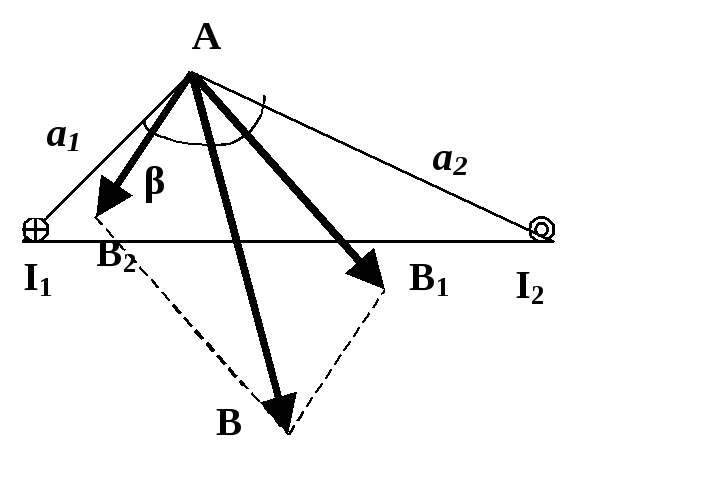ешение.Согласно принципу суперпозиции полей магнитная индукция в точкеАравна векторной сумме магнитных индукций, созданных каждым током в отдельности:

Однако здесь, в отличие от предыдущей задачи, точка А, в которой надо определить поле, и оба параллельных провода не лежат в одной плоскости. Поэтому векторы,не коллинеарны. Пусть они образуют уголα. Тогда модуль вектораВна основании теоремы косинусов

(1)

Величины В₁иВ₂можно найти по формуле для определения магнитной индукции в произвольной точкеАполя, созданного прямолинейным проводником с токомI:

, (2)

где φ₁,φ₂– углы, образованные радиусом-вектором, проведенным в точкуАсоответственно из начала и конца проводника, с направлением тока.

Так как в условии задачи речь идет о длинных проводниках, то ясно, что точка Аудалена от концов каждого провода на значительно большее расстояние, чем от самого провода. При этомφ₁= 0, аφ₂ = π. Тогда получим

(3)

Чтобы определить cos α, входящий в формулу (1), учтем, что каждый из векторов,лежит в плоскости, перпендикулярной соответствующему проводнику с током. Поэтому на схеме, выполненной в плоскости, содержащей векторы,, оба проводника проектируются в точки. В соответствии с принятым обозначением токI₁показан направленным от наблюдателя, токI₂– к наблюдателю. Векторы,изображены на схеме так, что их направление связано с направлением соответствующих токов правилом правого винта.

Пусть угол между отрезками а₁,а₂равенβ. Поскольку каждый из векторов,перпендикулярен соответствующему отрезку, должно выполняться равенство

α + β = π(4)

По теореме косинусов имеем

(5)

Из соотношений (4) и (5) следует

(6)

Подставив в (1) значения В₁,В₂, oпределяемые по формуле (3), а такжеcosαиз (6), найдем

Подставив числовые значения величин (все они даны в СИ) и произведя вычисление, получим ответ:

мкТл.

Пример 3. В однородном магнитном поле с индукцией 10  10^–2 Тл расположена прямоугольная рамка аbc, подвижная сторона которой ad длиной 0,1 м перемещается со скоростью 25 м/с перпендикулярно линиям индукции поля. Определить ЭДС индукции, возникающую в контуре аbcd.

Решение. Задачу можно решить двумя способами, применяя закон Фарадея для электромагнитной индукции или рассматривая силы, действующие на свободные электроны в движущейся проволоке (силы Лоренца).

1. При движении проводника аdплощадь рамки увеличивается, магнитный потокФсквозь рамку возрастает, а значит, согласно закону Фарадея

(1)

в рамке должна при этом действовать ЭДС индукции. Чтобы ее найти, сначала выразим магнитный поток Фчерез индукцию поляВи стороны рамкиL,x.

Согласно формуле для определения потока вектора магнитной индукции сквозь поверхностьSимеем

Ф = ВS = BLx.

Подставив это значение Фв (1) и учитывая, чтоВ,L– величины постоянные, запишем

где dx/dt = V–cкорость перемещения проводникаad. Поэтому

(2)

Сделав подстановку числовых значений величин B, L, V, получим ответ:

ε = –25 мВ.

Знак «минус» в формуле (2) показывает, что ЭДС индукции действует в контуре в таком направлении, при котором связанная с ним правилом правого винта нормаль к контуру противоположна вектору (т. е. направлена к наблюдателю на схеме). Значит, индукционный ток направлен в контуре против часовой стрелки.

2. Согласно определению,

, (3)

где q– величина заряда.

При движении в магнитном поле проводника adвместе с ним движутся со скоростьюVего свободные заряды (электроны). Поэтому на каждый из них действует сила Лоренца, выполняющая роль сторонней силы. Посколькуперпендикулярна, то сила Лоренца

F = qVB.

Так как она действует только вдоль участка adдлинойL, интеграл, стоящий в (3),

Подставив это значение интеграла в формулу (3), получим

(4)

что совпадает (по абсолютному значению) с формулой (2).

Пример 4. На проволочный виток радиусом 0.1 м, помещенный между полюсами магнита, действует максимальный механический момент 0.65  10^–5 Н  м. Сила тока в витке 2 А. Определить напряженность поля между полюсами магнита. Действием магнитного поля Земли пренебречь.

Решение. Напряженность Н магнитного поля можно определить из выражения механического моментаМ, действующего на виток с током в магнитном поле

(1)

где p_m– магнитный момент витка с током;B– индукция магнитного поля;α– угол между направлением напряженности магнитного поля и нормали к плоскости витка.

Если учесть, что максимальное значение механический момент принимает при sin α = 1и магнитный момент витка с током имеет выражение

p_m = I  S,

где S = π·R²– площадь, то формула (1) примет вид

M = μ·μ₀·ISH. (2)

Отсюда

(3)

Подставив в (3) числовые значения, получим

А/м.

Пример 5. Если сила тока, проходящего в некотором соленоиде, изменяется на 50 А в секунду, то на концах соленоида возникает ЭДС самоиндукции, равная 0.08 В. Определить по этим данным индуктивность соленоида.

Решение.Индуктивность имеет следующий физический смысл: она численно равна ЭДС самоиндукции, возникающей на концах соленоида в момент, когда ток, проходящий через соленоид, меняется на единицу силы тока в единицу времени. Математически это выражается известным законом Фарадея – Максвелла, примененным к ЭДС самоиндукции,

Вынося постоянную величину Lза знак дифференциала, получим

Отсюда, опуская знак «минус», найдем

.

Подставив числовые значения, получим

Гн.

Пример 6. Определить ЭДС индукции, возникающую на концах крыльев турбореактивного самолета, движущегося горизонтально со скоростью 900 км/ч, если размах крыльев самолета 36.5 м, а вертикальная составляющая напряженности магнитного поля Земли 39.85 А/м.

Решение. ЭДС индукции можно определить по формуле

.

По условию задачи α = 90^○, поэтому

.

Индукцию магнитного поля найдем из условия

где μ = 1(для воздуха);μ₀= 4π  10^–7Гн/м.

Тогда получим

Подставим числовые значения в системе СИ:

В.

Пример 7. Колебательный контур, состоящий из воздушного конденсатора с двумя пластинами по 100 см² каждая и катушки с индуктивностью 1000 см, резонирует на волну длиной 10 м. Определить расстояние между пластинами конденсатора.

Решение. Расстояние между пластинами конденсатора можно найти из формулы емкости плоского конденсатора

где ε– относительная диэлектрическая проницаемость среды, заполняющей конденсатор;S– площадь пластины конденсатора;d– расстояние между пластинами. Отсюда

.

Емкость найдем из формулы Томсона, определяющей период колебаний в электрическом контуре:

где L– индуктивность катушки.

Отсюда

Неизвестный в условии задачи период колебаний Tможно определить, зная длину волныλ, на которую резонирует контур.

Длина волны связана с периодом соотношением

λ =cT,

где с– скорость света в вакууме.

Отсюда

T = λ / с.

Подставив выражение TвC, а затем выражение емкостиC– вd, получим

В системе СИ:

S = 100 см² = 10^–2 м²;

L = 1000 см =1000  10^–9 Гн;

c = 3  10⁸ м/с;

λ = 10 м;

ε = 1;

Ф/м.

Подставив числовые значения в d, получим

м.

Пример 8. В сеть переменного тока напряжением 110 В включены последовательно конденсатор емкостью 5·10^–5 Ф, а также катушка с индуктивностью 200 мГн и активным сопротивлением 4 Ом.

Определить:

а) эффективную силу тока в цепи, если частота переменного тока 100  Гц;

б) частоту переменного тока, при которой в данном контуре наступит резонанс напряжений;

в) силу тока в цепи и напряжение на зажимах катушки и на пластинах конденсатора при наступлении резонанса напряжений.

Решение. а) Сила тока в цепи, содержащей индуктивность, емкость и активное сопротивление, определяется по формуле

(1)

где U_эф– эффективное напряжение переменного тока; – полное сопротивление; R– активное сопротивление цепи; – общее реактивное сопротивление;ω = 2πν– круговая частота переменного тока;ωL– реактивное индуктивное сопротивление;– реактивное емкостное сопротивление.

Подставив в (1) числовые значения величин, получим

А.

б) Резонанс напряжений наступает при условии равенства частоты переменного тока и частоты собственных колебаний контура:

(2)

Подставив в (2) числовые значения LиC, получим

Гц.

в) При резонансе емкостное и индуктивное сопротивления равны между собой, а общее реактивное сопротивление равно нулю, т. е.

Следовательно, полное сопротивление цепи при резонансе

Сила тока при резонансе

А.

Напряжение U_Lна зажимах катушки и напряжениеU_Cна пластинах конденсатора в момент наступления резонанса равны, так как в этот момент равны реактивные сопротивления катушки и конденсатора

В численном выражении

В.