16

Статистическая физика и термодинамика

Лекция 15

3. Функции распределения

3.1. Вероятность и флуктуации

Отличительной особенностью внутреннего движения частиц макроскопических тел является его случайный характер. Такая неопределенность характерна для микроскопического подхода к внутреннему движению большего числа частиц, составляющих тела.

В таких случаях говорят о вероятности того, что какие-либо физические величины будут иметь те или иные значения.

Термодинамическая вероятность – число способов, которыми может быть реализовано данное состояние макроскопической физической системы.

Каждое состояние физической системы с определенным распределением ее частиц по возможным классическим или квантовым состояниям называют микросостоянием.

Термодинамическая вероятность W равна числу микросостояний, реализованных в данном макросостоянии, т. е. W  1.

Вероятность дает наиболее правдоподобную оценку доли случайных событий с данным исходом при большом числе их повторений.

Наличие случайных отклонений от наиболее правдоподобного значения является причиной возникновения флуктуаций.

В теории вероятности установлено, что наиболее вероятными являются малые флуктуации.

Флуктуации физической системы, находящейся в состоянии термодинамического равновесия, всегда малы и имеют статистическую природу.

3.2. Распределение Максвелла

В состоянии термодинамического равновесия частицы физической системы движутся в основном со скоростями, близкими к скорости их теплового движения.

Все частицы перемещаются с различными скоростями, движение которых подчиняется законам классической физики.

Найдем функцию вероятности распределения молекул идеального газа по скоростям.

Задача заключается в том, чтобы найти вероятность dW(v) обнаружения частицы, значение скорости которой заключено в интервале (v; v + dv).

Мерой интервала является малый объем

dV = dv_x dv_y dv_z

в пространстве скоростей (v – пространство), в котором по координатным осям откладываются проекции скорости v_x, v_y, v_z.

Следовательно,

dW(v) = f(v) dv, (3.1)

где f(v) – плотность вероятности, или функция вероятности распределения молекул по скоростям.

В связи с тем, что в данный момент времени любая молекула имеет вполне определенное значение скорости, то должно выполняться условие нормировки, т. е.

.

Функция вероятности распределения молекул по скоростям

, (3.2)

где k – постоянная Больцмана; m₀ – масса одной молекулы; е – основание натуральных логарифмов (е = 2,72).

Полученный результат справедлив не только для газа, но и любого тела, находящего в состоянии термодинамического равновесия, если движение его частиц подчиняется классическим законам, т. е. вид распределения не зависит от того, как взаимодействуют частицы между собой.

Определяющим фактором здесь является способность частиц обмениваться энергией при переходе к равновесному состоянию.

Следовательно, вероятность обнаружить частицу с некоторой скоростью в пределах интервала (v; v + dv), описывается функцией

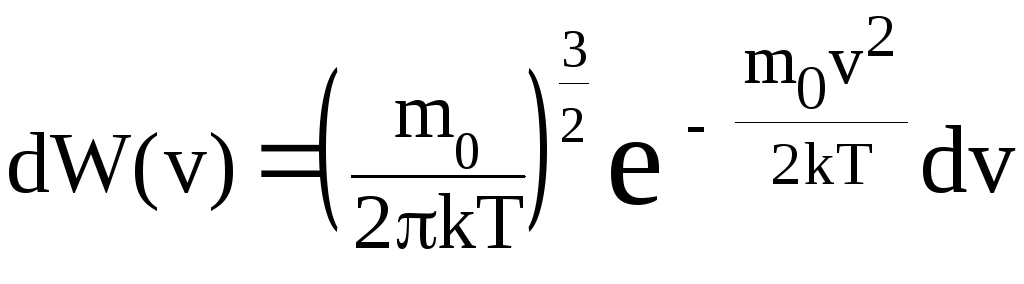. (3.3)

Формула (3.3) выражает распределение Максвелла для скоростей молекул.

Его справедливость ограничена областью применения законов классической физики для теплового движения.

Согласно (3.2), функция вероятности распределения зависит только от величины скорости. В рассматриваемой системе координат (v – пространство) интервал (v; v + dv) можно изобразить в виде сферического слоя (внутренний радиус сферического слоя – v, внешний – dv).

По предположению, толщина слоя интервала (v; v + dv) – мала.

Поэтому при суммировании вероятностей dW(v) в пределах сферического слоя функция распределения остается неизменной.

Тогда суммарный объем всех элементарных объемов сферического слоя V = 4v²dv.

Вывод: Для тел, находящихся в состоянии термодинамического равновесия, вероятность dW(v) обнаружить частицу этого тела со скоростью движения, абсолютное значение которой заключено в интервале (v; v + dv),

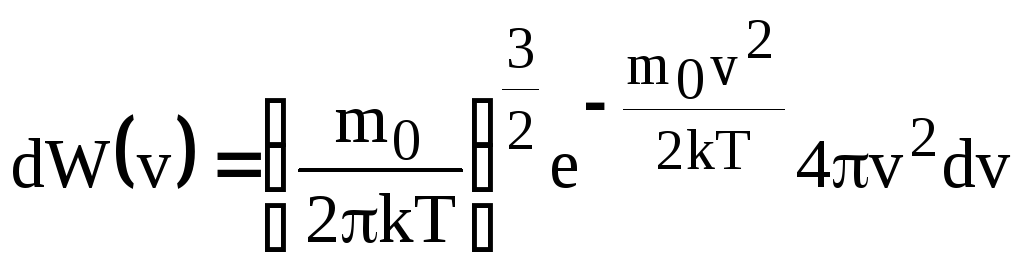. (3.4)

Полученную формулу называют распределением Максвелла по абсолютным значениям скоростей, плотность вероятности, которой

(v) = 4v²f(v) =

имеет вид

, (3.5)

где dW(v) = (v)dv =

– вероятность того, что модуль скорости молекулы заключен в интервале (v; v + dv).

Рис. 14.1

График зависимости (v) приведен на рис. 3.1.

Величину скорости, при которой функция (v) максимальна, называют наиболее вероятной скоростью v_в. Дифференцируя выражение (3.5) по аргументу v² и приравняв его нулю, получим

.

Из последнего выражения следует, что наиболее вероятная скорость

. (3.6)

Максимум кривой на рис. 3.1 соответствует значению наиболее вероятной скорости v_в.

Из формулы (3.6) следует, что при увеличении температуры идеального газа (или уменьшении массы молекулы) максимум кривой смещается вправо и становится ниже при неизменной площади под кривой, а доля молекул, имеющие малые скорости, уменьшается, напротив – доля молекул с большими скоростями увеличивается.

Средняя арифметическая скорость молекул

или .

Интегрируя последнее выражение с учетом (2.5), получаем

. (3.7)

Средняя квадратичная скорость – квадратный корень из среднего значения квадрата тепловой скорости поступательного движения молекулы <v_кв> = , где.

Давление, производимое молекулами при их тепловом хаотическом движении на стенки сосуда, в котором они находятся,

или , где = nm₀.

При постоянной температуре газа, применяя уравнение состояния идеального газа в виде

или ,

получаем

. (3.8)

Средняя квадратичная скорость не имеет смысла для одной молекулы, а характеризует движение всей совокупности молекул.

При t = 0 ^оC cредняя квадратичная скорость:

для азота – <v_кв> = 493 м/c;

для водорода – <v_кв> = 1838 м/c;

для кислорода – <v_кв> = 461 м/c.

Замечание: Средняя квадратичная скорость такого же порядка, что и скорость звука в газе, так как передача возмущений в звуковой волне осуществляется молекулами, движущимися с тепловыми скоростями.

Это же относится и к скорости истечения газа в вакуум.

Таким образом, все три скорости <v>, <v_кв> и v_в характеризуют тепловое движение молекул газа и различаются только числовыми коэффициентами

(3.9)

Изучение вероятности распределения теплового движения молекул по скоростям (распределение Максвелла) осуществлялось различными экспериментальными методами (опыты Штерна, Ламмерта и др.).

Для проведения эксперимента молекулярные пучки получают выпусканием в вакуумную камеру пучка молекул или атомов, исследуемого вещества, испаряющихся с нагревателя специальной печи.

При исследовании молекулярных (атомных) пучков используют физическое явление – эффузию газов: медленное истечение газов через малые отверстия.

От распределения молекул идеального газа по скоростям (распределение Максвелла) можно перейти к вероятности распределения молекул по значениям их кинетической энергии, т. е.

. (3.10)

Формула (13.10) выражает вероятность dW(_к) обнаружить частицу со значением кинетической энергии из интервала (_к; _к + d_к).