7.3. Кинематика движущейся жидкости

При движении жидкости можно проследить, что происходит с течением времени в каждой ее точке, т. е. можно указать величину и направление скорости движения различных частиц жидкости, которые в разные моменты времени проходят через одну и ту же точку пространства. При фиксированном времени в пространстве возникает мгновенная картина распределения скоростей жидкости – поле скоростей.

Следовательно, в каждой точке пространства можно указать вектор скорости любой частицы, проходящей через эту точку в данный момент времени.

Рис. 7.4

Линию, касательная к которой указывает направление скорости движения частицы, проходящей в рассматриваемый момент времени через эту точку касания, называют линией тока.

Если поле скоростей и соответствующие ему линии тока, не изменяются с течением времени, то движение жидкости называют стационарным.

Рассмотрим произвольный замкнутый контур L, в котором через каждую его точку, в один и тот же момент времени, проведены линии тока (рис. 7.4).

Они образуют поверхность, называемую трубкой тока.

Скорости частиц жидкости направлены по касательным к линиям тока.

При течении жидкости они не пересекают боковой поверхности трубки тока.

На такие трубки тока можно разбить все пространство, занимаемое жидкостью.

Если поперечное сечение трубки тока бесконечно мало, то скорость частиц жидкости будет направлена вдоль оси трубки тока.

Массу жидкости, протекающую через поперечное сечение трубки тока за время dt, можно определить по формуле

dm = S(vdt), (7.18)

где  – плотность жидкости; S – площадь поперечного сечения трубки тока, нормально расположенной к линиям тока.

Для сечений трубки тока при стационарном течении жидкости dm = сonst.

Для двух произвольных поперечных сечений трубки тока S₁ и S₂ (рис. 7.4) выполняется равенство

₁v₁S₁ = ₂v₂S₂ (7.19)

Если жидкость несжимаема, то

₁ = ₂,

тогда формула (7.19) принимает вид

v₁S₁ = v₂S₂, (7.20)

т. е. скорость течения жидкости обратно пропорциональна площади поперечного сечения трубки тока.

7.4. Стационарное движение идеальной жидкости

Вследствие малой сжимаемости жидкости во многих случаях можно полностью пренебречь изменением ее объема, т. е. можно говорить об абсолютно несжимаемой жидкости.

Жидкость, в которой при любых движениях не возникают силы внутреннего трения, называют идеальной.

В идеальной жидкости могут существовать только силы нормального давления, которые можно вычислить с помощью уравнения состояния

Р = f(, T). (7.21)

Если жидкость находится в движении, то наряду с нормальным напряжением в ней могут возникнуть и касательные силы, которые определяются скоростью деформации жидкости, т. е. равны производным деформации по времени. Поэтому их относят к разряду сил трения, или вязкости.

Рассмотрим стационарное движение идеальной жидкости в потенциальном поле сил (например, поле силы тяжести).

Работа, совершаемая силами давления при перемещении некоторой массы жидкости

(7.22)

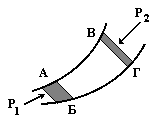
где А₁ – работа по перемещению левой границы АБ объема жидкости; А₂ – работа по перемещению правой границы ВГ объема жидкости против давления Р₂ (рис. 7.5); m – масса жидкости; ₁ и ₂ – плотности жидкости слева и справа в рассматриваемом объеме, соответственно.

Эта работа равна приращению полной энергии W, рассматриваемого объема жидкости (закон сохранения энергии для стационарного движения жидкости).

Рис. 7.5

Изменение полной энергии

W = (w₂ – w₁) m, (7.23)

где w₁, w₂ – полные энергии, приходящиеся на единицу массы жидкости до и после перемещения соответственно. Используя формулы (7.22) и (7.23),получаем

. (7.24)

Следовательно, при стационарном течении идеальной жидкости вдоль одной и той же линии тока, величина остается постоянной.

Рис. 7.6

Полученную формулу (7.24) называют уравнением Д. Бернулли, которое справедливо и для сжимаемой жидкости.

Если жидкость несжимаема, то при ее течении не изменяется та часть полной энергии w, которая зависит от степени сжатия жидкости.

Вся полная энергия w состоит из кинетической энергии и потенциальной энергии в поле силы тяжести w_р= gh. Поэтому уравнение Бернулли принимает вид

. (7.25)

Если тонкая трубка тока имеет переменное сечение (ее ось – горизонтальна), то h = сonst и уравнение (7.25) принимает более простой вид:

. (7.26)

Вывод: Давление в сечении трубки тем больше, чем меньше скорость течения жидкости. Согласно (7.26), скорость минимальна там, где максимально сечение трубки. Следовательно, в широких частях трубки давление максимально, а в узких – минимально.

На основании уравнений (7.26) и (7.24) можно сказать, когда при течении жидкости или газа они являются несжимаемыми.

Если рассматривать истечение идеальной несжимаемой жидкости через малое отверстие в боковой стенке или на дне сосуда, то частицы жидкости подходят к отверстию, имея скорость в поперечных направлениях. Из-за инерции это вызывает сжатие вытекающей струи (рис. 7.6).

Чтобы этого не наблюдалось, у отверстия закругляют края. Поэтому линии тока перед истечением постепенно изменяют направление на параллельные оси трубки, и сжатие струи не происходит (за исключением небольшого сжатия, вызванного силами поверхностного натяжения). Применив уравнение Д. Бернулли к точкам А и Б произвольной линии тока (рис. 7.6), получим равенство

(7.27)

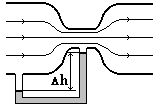
Рис. 7.7

где v – скорость жидкости в точке Б ( в точке А скорость пренебрежимо мала); Р₀ – атмосферное давление; h – высота столба жидкости.

Из (7.27) имеем

v² = 2gh. (7.28)

Равенство (7.28) называется формулой Торричелли.

Для измерения скорости потока жидкости (газа) используют трубку Вентури (рис. 7.7).