2.2. Пружинный маятник

Если колебательная система совершает гармонические колебания, имея одну степень свободы, то она называется линейным классическим гармоническим осциллятором.

Примерами классического линейного осциллятора являются пружинный маятник, математический, физический маятники и др.

Рассмотрим колебания пружинного маятника.

Пружинный маятник представляет собой некоторый груз массой m, закрепленный на пружине с коэффициентом жесткости k, совершающий свободные гармонические колебания (рис. 2.2).

Гармонические колебания называют свободными, если они совершаются только под действием сил, вызывающих эти колебания.

Частоту свободных гармонических колебаний называют собственной частотой (₀), так как она зависит только от свойств самой физической системы.

Найдем дифференциальное уравнение свободных гармонических колебаний пружинного маятника. На маятник действует сила тяжести

G = mg

и сила упругости (закон Гука, рис. 2.2) F_упр = – кх,

Рис. 2.2

где х – смещение ; k – коэффициент жесткости (упругости) пружины.

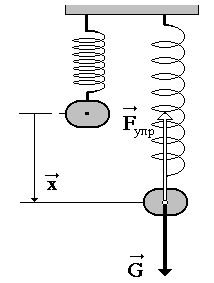
Эти силы в состоянии покоя равны по величине, но противоположны по направлению (третий закон Ньютона).

Однако при колебаниях сила упругости изменяется периодически по величине и по направлению.

Значит, силой, вызывающей колебания пружинного маятника, является сила упругости.

При этом выполняется следующее соотношение:

ma_х = – kx,

где

,

тогда . (2.1)

Последнее выражение приведем к нормальному виду однородного дифференциального уравнения второго порядка, описывающего одномерное (с одной степенью свободы) движение пружинного маятника, например, вдоль оси Х:

. (2.2)

Решением данного дифференциального уравнения является функция

х = Асos (_оt + _o). (2.3)

Выразим k в уравнении (2.2) через собственную круговую частоту ₀ и смещение х.

Для этого достаточно вспомнить, что ускорение

. (2.4)

Используя выражения (2.1) и (2.4), запишем, что

F = ma =  m _о²х. (2.5)

С другой стороны, при колебаниях пружинного маятника роль действующей силы выполняет сила упругости (речь о ней шла выше)

F_упр = – кх. (2.6)

Из соотношений (2.5) и (2.6) имеем

 m _о²х = – кх.

После несложных преобразований получим

k = m _о². (2.7)

Дифференциальное уравнение (6.24) принимает следующий вид:

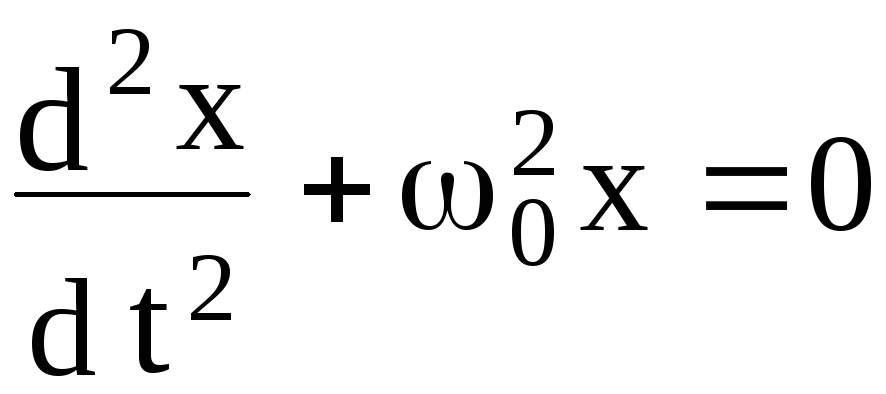. (2.8)

Напомним, что уравнение вида (2.8) является общим для всех физических систем различной природы, совершающих свободные гармонические колебания, только вместо смещения х используется величина, характеризующая колебания данной системы, например, колебание заряда (q), тока (I) и т. д. Сравнивая общее дифференциальное уравнение гармонических колебаний (2.8) и дифференциальное уравнение колебаний пружинного маятника (2.2), приходим к заключению, что квадрат круговой частоты прямо пропорционален коэффициенту жесткости пружины и обратно пропорционален его массе:

(2.9)

Найдем период колебаний пружинного маятника.

Из кинематики вращательного движения известно, что период и угловая скорость (круговая частота) связаны соотношением

T = .

Следовательно, период колебаний пружинного маятника

. (2.10)

Вывод: Период колебаний пружинного маятника прямо пропорционален квадратному корню массы маятника и обратно пропорционален квадратному корню коэффициента жесткости пружины.

Замечание: Выводы, полученные при рассмотрении колебаний пружинного маятника, можно использовать в задачах, связанных с колебаниями атомов и молекул различных физических систем.