2. Разность фаз складываемых взаимно перпендикулярных колебаний равна нечетному числу /2, т. Е.

 = (2m + 1) / 2, где m = 0, 1, 2, 3, ... .

Например, при m = 0,  = /2. После подстановки  = ₀ в выражеие (1.18) получаем уравнение эллипса с направлением осей вдоль Х и У, полуоси которого соответственно равны амплитудам А и В (рис. 1.16):

.

Рис. 1.16

Замечание: При равенстве амплитуд А = В складываемых колебаний эллипс вырождается в окружность радиуса R (А = В = R):

х² + у² = R².

В этом случае результирующее колебание называют поляризованным по кругу. Выясним, в каком направлении частица будет двигаться по эллипсу или окружности в результате сложения взаимно перпендикулярных колебаний при разности фаз, равной  /2.

Для этого уравнения (1.17) представим в виде

х = А cos t, y = Bcos(t + /2) =  B sin t. (1.21)

б

а

Если  = +  / 2, то при t = 0 частица будет находиться в состоянии 1 (рис. 1.17, а).

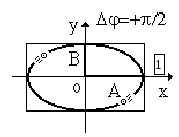
Рис. 1.17

По мере движения частицы по траектории, согласно выражению (1.21), координата х убывает, а координата у принимает отрицательные значения.

Следовательно, частица движется по траектории по часовой стрелке.

При  =  /2 уравнения (1.17) запишутся в виде

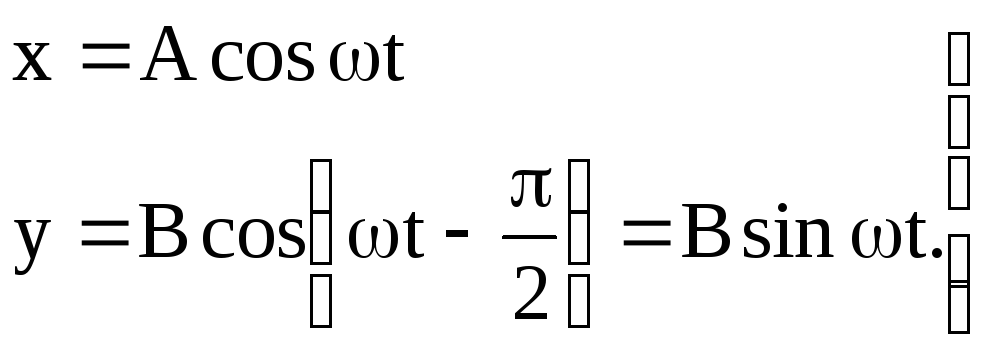. (1.22)

Следовательно, частица будет двигаться по траектории против часовой стрелки (рис. 1.17, б).

1.9. Фигуры Лиссажу

При сложении взаимно перпендикулярных колебаний с различными амплитудами и частотами ₁  ₂ и неодинаковыми начальными фазами возникают сложные результирующие колебания, которые называют фигурами Лиссажу.

Наблюдение фигур Лиссажу осуществляется, например, при сложении взаимно перпендикулярных электрических колебаний.

Если отношение круговых частот

Рис. 1.18

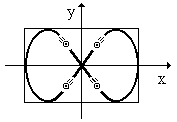
и разность фаз складываемых колебаний

 = /2,

наблюдается кривая, напоминающая восьмерку (рис. 1.18).

При отношении круговых частот

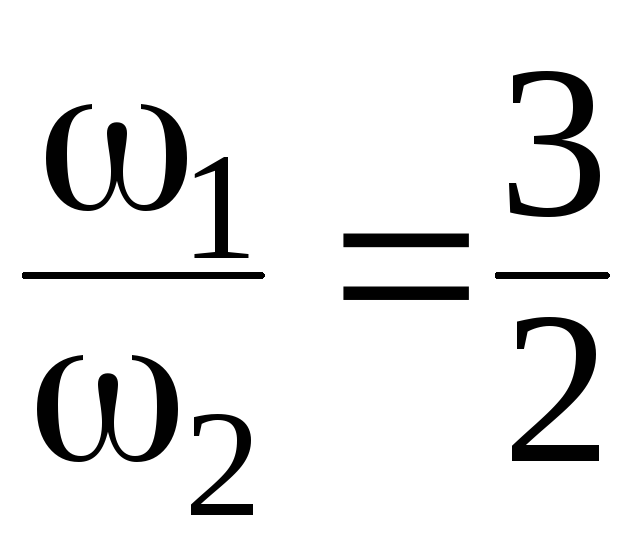
и разности фаз складываемых колебаний  = /2 наблюдается более сложная кривая (рис. 1.19).

Рис. 1.19

Замечание 1: Число касаний фигуры Лиссажу со сторонами прямоугольниика, образованного амплитудами, равно величине отношения частот.

Замечание 2: Если частоты складываемых колебаний кратны n и m, тогда уравнения взаимно перпендикулярных колебаний запишутся в виде

. (1.23)

Величины координат колеблющейся частицы одновременно повторяются через одинаковые промежутки времени, равные периоду Т, как наименьшему кратному периодов Т₁ = 2/(n) и Т₂ = 2/(m), соответствующие периодам колебаний вдоль осей Х и У.

Траектория результирующего колебания будет замкнутой, её форма зависит от амплитуд А и В, круговых частот n и m и значений начальных фаз ₀₁ и ₀₂.