
- •1. Кинематика гармонических колебаний
- •1.1. Колебательные процессы
- •1.2. Уравнение скорости материальной точки,
- •1.3. Уравнение ускорения материальной точки,
- •1.4. Начальные условия
- •1.5. Метод векторных диаграмм
- •1.6. Сложение колебаний одного направления
- •1.7. Биения
- •1.8. Сложение взаимно перпендикулярных колебаний
- •2. Разность фаз складываемых взаимно перпендикулярных колебаний равна нечетному числу /2, т. Е.
- •1.9. Фигуры Лиссажу
- •1.10. Представление колебаний в комплексной форме
- •2. Гармонический осциллятор
- •2.2. Пружинный маятник
- •Используя выражения (2.1) и (2.4), запишем, что
- •2.3. Физический маятник
- •2.4. Математический маятник
- •2.5. Приведенная длина физического маятника
- •2.6. Энергия гармонических механических колебаний
- •2.6.1. Кинетическая энергия
- •2.6.2. Потенциальная энергия
- •2.6.3. Полная энергия гармонических колебаний
- •2.7. Затухающие гармонические колебания
- •2.8. Основные параметры затухающих колебаний
- •2.9. Понятие о связанных гармонических осцилляторах
- •Используя метод характеристического уравнения, решения уравнений (2.43) и (2.44) запишем в виде: (2.45)
1.2. Уравнение скорости материальной точки,
совершающей гармонические колебания
Если в качестве колебательной системы использовать, например, математический маятник (рис. 1.3), то в процессе его движения происходит периодическое изменение скорости и ускорения.
При движении маятника, после прохождения им положения равновесия, в направлении к состоянию I (в ту же сторону направлен и вектор скорости маятника) скорость убывает, а ускорение растет и в крайнем состоянии
Рис.
1.3
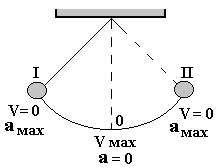
Модуль скорости растет по величине, а ускорение убывает (направление вектора ускорения теперь совпадает с направлением движения маятника). При достижении положения равновесия в точке 0 скорость достигает максимума, - ускорение обращается в нуль.
После прохождения этого состояния скорость начинает убывать, а ускорение увеличивается (теперь вектор ускорения направлен к состоянию покоя со стороны состояния II и противоположен вектору скорости). При достижении крайнего положения II скорость обращается в нуль, ускорение достигает максимума. При движении маятника из состояния II снова к положению равновесия скорость, изменив направление, растет, соответственно ускорение, сохраняя направление, убывает. В точке 0 скорость маятника максимальна, ускорение обращается в нуль. При дальнейшем движении маятника весь процесс периодически повторяется. Найдем уравнения изменения скорости и ускорения маятника при гармонических колебаниях. Дифференцируя уравнение смещения (1.1) по времени t, найдем уравнение изменения скорости в любой момент времени (первая производная):
V
=![]() =
Asin
(t
+ o)
=
Asin
(t
+ o)
или
![]() (1.2)
(1.2)
где (wА) – амплитудное значение скорости м. т., совершающей гармонические колебания.
Скорость опережает смещение по фазе на / 2 или отстает на 3 / 2.
Вывод: Скорость м. т. при колебательных процессах изменяется по гармоническому закону и является функцией времени.
1.3. Уравнение ускорения материальной точки,
совершающей гармонические колебания
Найдем уравнение изменения ускорения как первую производную скорости по времени (вторая производная смещения по времени):
Рис. 1.4

![]() .
(1.3)
.
(1.3)
или
![]() .
.
Используя уравнение (6.1) получим, что
а = 2х . (1.4)
Вывод: Ускорение изменяется по гармоническому закону, является функцией времени и опережает колебания смещения по фазе на и опережает колебание скорости по фазе на /2.
Величина 2А является амплитудным значением ускорения. На рис. 1.4, а, б, в приведены графики смещения, скорости и ускорения как функций времени.
1.4. Начальные условия
Величину амплитуды А и значение начальной фазы найдем, если в уравнениях (1.1) и (1.2) положить начальный момент времени t = 0.
Тогда уравнения примут вид
хо = Асosо, vo = Asinо.
Решая эти уравнения совместно, найдем амплитуду и начальную фазу, если известны хо и vo.
Действительно, после преобразований, имеем
хо2 = А2cos2о,
vo2 = А2 sin2о
или
![]() .
.
Следовательно,
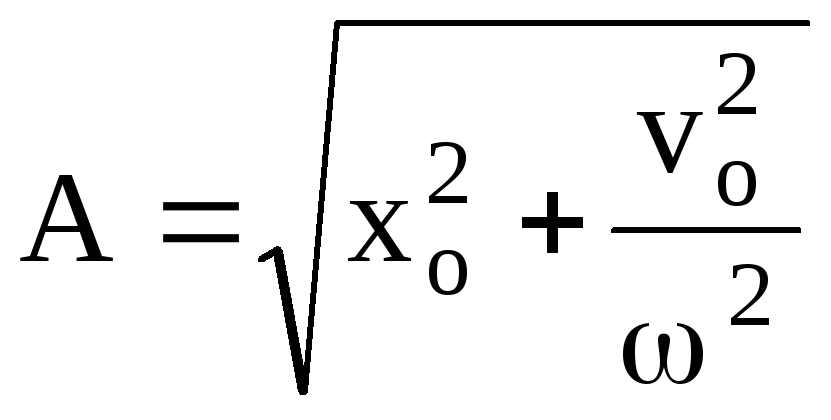 ;
;
![]() .
.
